C程序设计实验报告
实验项目:
一.函数的定义和调用
1.编写由三角形三边求面积的函数。
2.编写求N阶乘的函数。
3.求两个整数的最大公约数。
4.打印输出指定图形。
二.模块化程序设计
1.求500以内的所有亲密数对。
姓名:李小玲 实验地点: 514实验室 实验时间:2019年4月30日
一、实验目的与要求
6.4.1.函数的定义和调用
实验1.编写由三角形三边求面积的函数
1.调用area()函数求三角形的面积;
2.在求面积函数中运用海伦公式。
实验2.编写求N阶乘的函数
1.定义符号常量
2.使用长整型变量存放累乘积
3.在函数中,使用局部静态变量存放累乘积
4.使用全局变量存放累乘积
实验3.求两个整数的最大公约数
1.调用gcd()函数求两个整数的最大公约数
2.掌握辗转相除法求两个整数的最大公约数
实验4.打印输出指定图形
1.调用trangle()函数输出三角形
2.在trangle()函数中用for循环的嵌套输出指定的结果
6.4.2.模块化程序设计
实验1.求500以内的所有亲密数对
1.掌握C语言中定义函数的方法
2.掌握通过“值传递”调用函数的方法
二、实验内容
6.4.1:用for语句实现循环
实验1:编写由三角形三边求面积的函数
1.问题的简单描述:编写程序,从键盘输入三角形的3条边,调用三角形面积函数求出其面积,并输出结果。
2.实验代码,流程图,效果图:
#include<math.h> #include<stdio.h> float area(float a,float b,float c) { float s,p,area; s=(a+b+c)/2; p=s*(s-a)*(s-b)*(s-c); area=sqrt(p); return(area); } main() { float x,y,z,ts; printf("please enter the value of :",x,y,z); scanf("%f%f%f",&x,&y,&z); ts=area(x,y,z); if((x+y)>z&&(x+z)>y&&(y+z)>x) printf("area=%f ",ts); else printf("data erroy!"); }
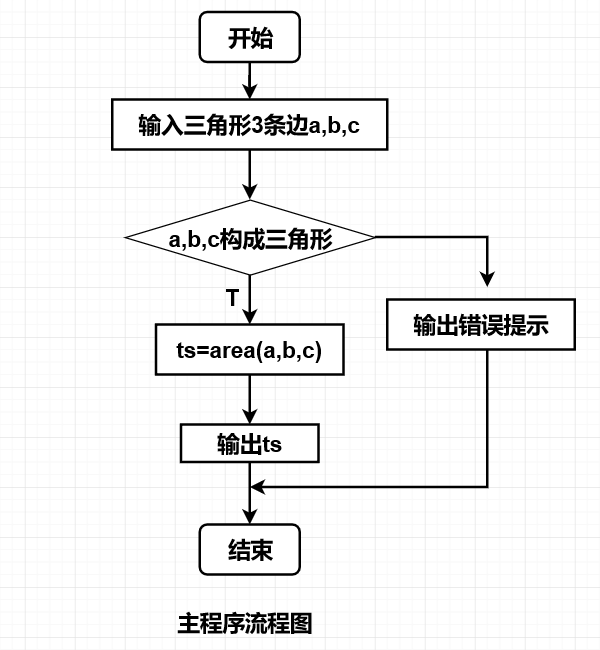
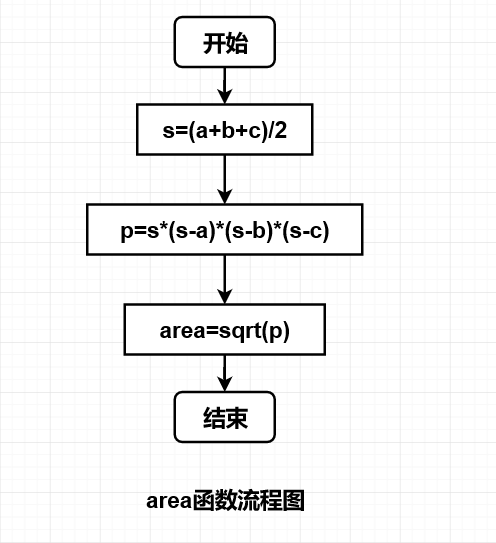
3.分析:开头的时候要记得用math.h,因为用到了开方函数,然后的话就是要注意计算三角形的面积公式,流程图里面有,最后是判断的时候要用C语言符号&&;这题不是很难但是要注意细节,比如说主函数和函数定义里面形参和实参不要搞混。
实验2:编写求N阶乘的函数
1.问题的简单描述:编写函数,求出从主调函数传来的数值i的阶乘值,然后将其传回主调函数并输出。
2.实验代码,流程图,效果图:
#include<math.h> #include<stdio.h> signed int N=5; long function(int i) { static long f=1; f=f*i; return f; } main() { long product; int i; for(i=1;i<=N;i++) { product=function(i); printf("%d的阶层是:%d ",i,product); } }
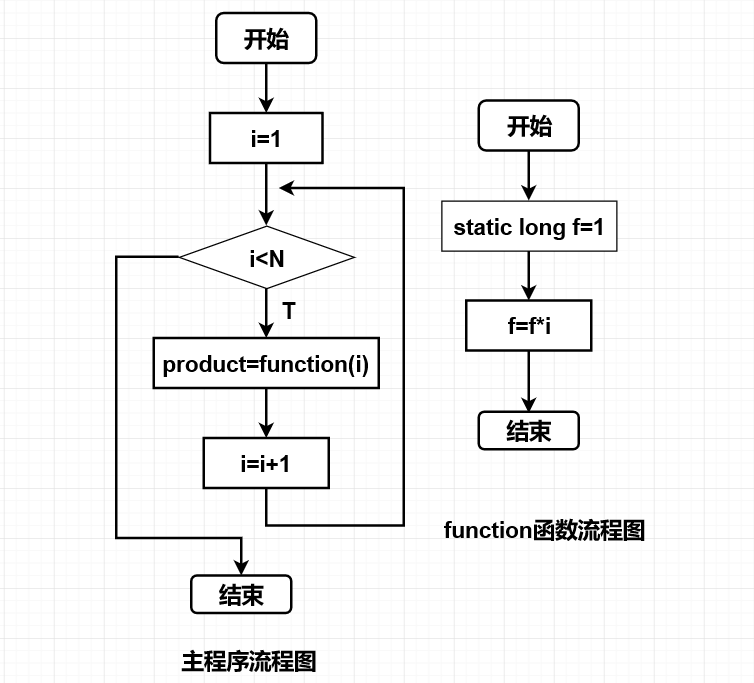
3.分析:这题的话我主要是输出的时候出现了问题,就是不知道格式,怎么才能输出i的阶乘是多少,并且i在1-5之间变化;因为i和product都会变,所以在它要变的地方,按照平时输出的方法其实就是可以了,其他的话,我觉得还好。
实验练习3:求两个整数的最大公约数
1.问题的简单描述:编写程序,从键盘输入两个整数,调用gcd()函数求它们的最大公约数,并输出结果。
2.实验代码,流程图,效果图:
#include<stdio.h> int gcd(int a,int b) { int temp; int remainder; if(a<b) { temp=a; a=b; b=temp; } remainder=a%b; while(remainder!=0) { a=b; b=remainder; remainder=a%b; } return b; } main() { int x,y; int fac; printf("please input two integers: ",x,y); scanf("%d%d",&x,&y); fac=gcd(x,y); printf("The great common divisor is:%d",fac); }
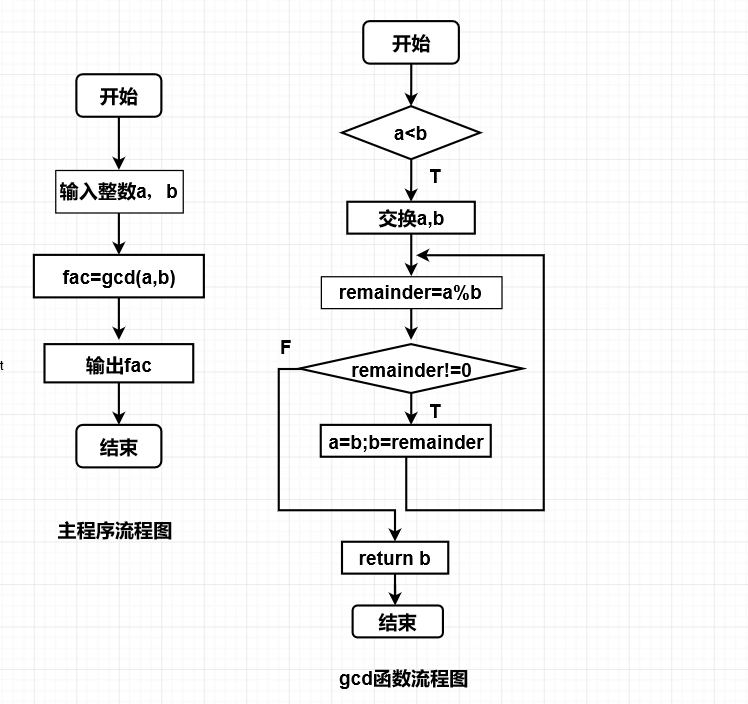
3.分析:求最大公约数,还是要先看懂辗转相除法的原理;例如,a>b,如果a能够被b整除,最大公约数就是b,如果a除以b的余数为c,则继续用b除以c,在反复进行,直到余数为0,它就是a,b的最大公约数。还有就是在while里面,也要用一次remainder=a%b,因为后面这个remainder就相当于c,就是a,b不能整除的这种情况。
实验练习4:打印输出指定图形
1.问题的简单描述:输入整数n,输出高度为n的等边三角形。当n=5时的等边三角形。
2.实验代码,流程图,效果图:
#include<stdio.h> void trangle (int n) { int i,j; for(i=0;i<n;i++) { for(j=0;j<n-i;j++) printf(" "); for(j=0;j<=2*i;j++) printf("*"); putchar(' '); } } main() { int n; printf("please enter the n: ",n); scanf("%d",&n); printf(" "); trangle(n); }
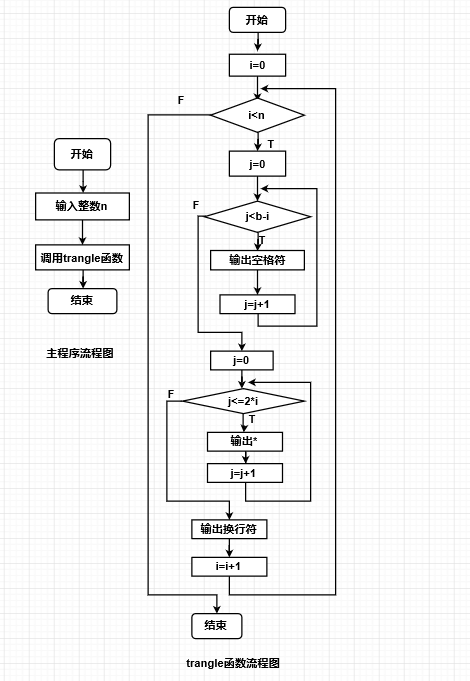
3.分析:这个三角形图形的在上一章节已经讲过,不同的就是它用的是函数的方法,还是要在函数的定义里面每行每列找出*和空格的规律,最后的话就是空格不要打多了,我就是打了两个空格,找了 半天的错误都没发现。
6.4.2:模块化程序设计
实验练习1:求500以内的所有亲密数对
1.问题的简单描述:若正整数A的所有因子(包括1担不包括自身,下同)之和为B,而B的因子之和为A,则称A和B为一对亲密数。例如:6的因子之和为1+2+3=6,因此6与6为一对亲密数(即6自身构成一对亲密数);又如,220的因子之和为1+2+3+4+5+10+11+20+22+44+55+110=284,而284的因子之和为1+2+4+71+142=220,因此,220与284为一对亲密数。
具体要求如下:
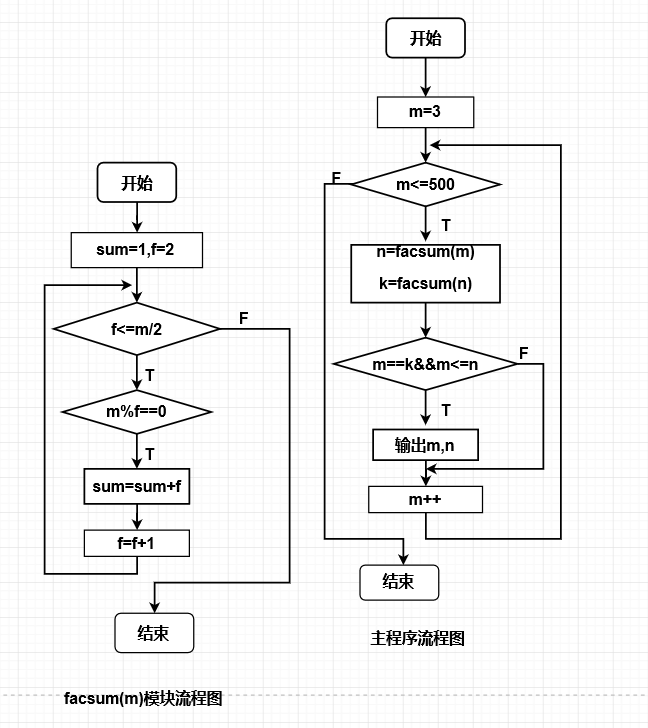
(1)编制一个函数facsum(m),返回给定正整数m的所有因子(包括1但不包括自身)之和。
(2)编制一个主函数,调用(1)中的函数facsum(),寻找并输出500以内的所有亲密数对。
(3)输出要有文字说明。在输出每对亲密数时,要求从小到大排列并去掉重复的亲密数对。
(4)所有函数中的循环均为for循环。
2.实验代码,流程图,效果图:
#include<stdio.h> int facsum(int m) { int sum=1,f=2; while(f<=m/2) { if(m%f==0) sum=sum+f; f++; } return sum; } main() { int m=3,n,k; while(m<=500) { n=facsum(m); k=facsum(n); if(m==k&&m<=n) printf(" %d %d ",m,n); m++; } }
3.分析:求亲密对数最最基本的肯定是要看懂什么事亲密对数,我刚开始的按照流程图去做的,可以出结果,但还得不太明白;这个程序现实用了facsum(m)的模块求出m所有的因子,再是n是所有m因子的相加也就是另一个数,再判断这另一个数的因子所有因子之和与m的关系,也就是判断这两个数是不是亲密对数的条件,又因为条件要从小到大排列,所以加了一个m<=n。不然结果会反过来就像下面:
三.实验小结
这次实验的数量虽然不是很多,但是像里面的辗转相除法和求亲密对数的方法对我们来说还是很有用的,最最大的问题就是我们做题的时候习惯性的看流程图,因为看流程图我们很快就能做出来,因为一些难的公式,和运算方法,它里面都有,所以我感觉我个人的话还是太依赖流程图了,因为做不出来的时候,第一反应是看下流程图,而不是自己思考;然后我以后遇到题目,尽量自己先做一下,在看流程图。