题目大意:
有一个8*8的正方形棋盘,每个格子有相对应的值,对于这个棋盘,我们可以割(n-1)次,使得切割后的n块棋盘权值和的标准差最小。
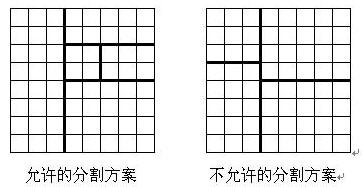
同时每次切割后下一次切割只能对上次被切割的其中一块进行切割,另一块就不能够再被切割了。
思路:
dp
首先可以注意到棋盘非常小,是8*8,n<15也并不大,先利用方差来计算,最后在用标准差
dp(x1,y1,x2,y2,k)表示(x1,y1) 为左上角(x2,y2)为右下角的矩形切k刀的答案。
首先,我们可以把方差的公式化简一下:
1/n(x1^2+x2^2+...+xn^2-2*x1*avg-2*x2*avg-...-2*xn*avg+n*avg*avg)
=1/n(x1^2+x2^2+...+xn^2-2*avg*sum+sum*avg)
=1/n(x1^2+x2^2+...+xn^2-n*avg*avg)
=(x1^2+x2^2+...+xn^2)/n-avg^2
因为所有矩阵的和一定,所以我们先预处理出avg,然后dp表示每块的答案就好了
先预处理每块不切的情况 即dp(x1,y1,x2,y2,0)=sum^2
然后最外圈套k
枚举每一块的切割线以及左右两边哪边是新切的
最后把dp(0,0,7,7,n-1)带入公式
就做完了哈哈哈

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<cstdlib> 6 #include<algorithm> 7 #include<iomanip> 8 #include<vector> 9 #include<queue> 10 #define long long ll 11 #define inf 214748364 12 using namespace std; 13 int n,map[9][9],sum[9][9]; 14 int f[9][9][9][9][17]; 15 double avg; 16 int main() 17 { 18 scanf("%d",&n); 19 for(int i=0;i<8;i++) 20 for(int j=0;j<8;j++) 21 { 22 scanf("%d",&map[i][j]); 23 sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+map[i][j]; 24 avg+=map[i][j]; 25 } 26 avg=1.0*avg/n; 27 for(int i1=0;i1<8;i1++) 28 for(int j1=0;j1<8;j1++) 29 for(int i2=i1;i2<8;i2++) 30 for(int j2=j1;j2<8;j2++) 31 { 32 int s=sum[i2][j2]-sum[i1-1][j2]-sum[i2][j1-1]+sum[i1-1][j1-1]; 33 f[i1][j1][i2][j2][0]=s*s; 34 } 35 for(int k=1;k<n;k++) 36 for(int i1=0;i1<8;i1++) 37 for(int j1=0;j1<8;j1++) 38 for(int i2=i1;i2<8;i2++) 39 for(int j2=j1;j2<8;j2++) 40 { 41 int d=1<<30; 42 for(int o=i1;o<i2;o++) 43 { 44 d=min(f[i1][j1][o][j2][0]+f[o+1][j1][i2][j2][k-1],d); 45 d=min(f[i1][j1][o][j2][k-1]+f[o+1][j1][i2][j2][0],d); 46 } 47 for(int o=j1;o<j2;o++) 48 { 49 d=min(f[i1][o+1][i2][j2][0]+f[i1][j1][i2][o][k-1],d); 50 d=min(f[i1][o+1][i2][j2][k-1]+f[i1][j1][i2][o][0],d); 51 } 52 f[i1][j1][i2][j2][k]=d; 53 } 54 double ans=f[0][0][7][7][n-1]; 55 ans=sqrt(ans/n-avg*avg); 56 printf("%.3lf",ans); 57 }
