描述
由于今天上课的老师讲的特别无聊,小Hi和小Ho偷偷地聊了起来。
小Ho:小Hi,你这学期有选什么课么?
小Hi:挺多的,比如XXX1,XXX2还有XXX3。本来想选YYY2的,但是好像没有先选过YYY1,不能选YYY2。
小Ho:先修课程真是个麻烦的东西呢。
小Hi:没错呢。好多课程都有先修课程,每次选课之前都得先查查有没有先修。教务公布的先修课程记录都是好多年前的,不但有重复的信息,好像很多都不正确了。
小Ho:课程太多了,教务也没法整理吧。他们也没法一个一个确认有没有写错。
小Hi:这不正是轮到小Ho你出马的时候了么!
小Ho:哎??
我们都知道大学的课程是可以自己选择的,每一个学期可以自由选择打算学习的课程。唯一限制我们选课是一些课程之间的顺序关系:有的难度很大的课程可能会有一些前置课程的要求。比如课程A是课程B的前置课程,则要求先学习完A课程,才可以选择B课程。大学的教务收集了所有课程的顺序关系,但由于系统故障,可能有一些信息出现了错误。现在小Ho把信息都告诉你,请你帮小Ho判断一下这些信息是否有误。错误的信息主要是指出现了"课程A是课程B的前置课程,同时课程B也是课程A的前置课程"这样的情况。当然"课程A是课程B的前置课程,课程B是课程C的前置课程,课程C是课程A的前置课程"这类也是错误的。
输入
第1行:1个整数T,表示数据的组数T(1 <= T <= 5)
接下来T组数据按照以下格式:
第1行:2个整数,N,M。N表示课程总数量,课程编号为1..N。M表示顺序关系的数量。1 <= N <= 100,000. 1 <= M <= 500,000
第2..M+1行:每行2个整数,A,B。表示课程A是课程B的前置课程。
输出
第1..T行:每行1个字符串,若该组信息无误,输出"Correct",若该组信息有误,输出"Wrong"。
- 样例输入
-
2 2 2 1 2 2 1 3 2 1 2 1 3
- 样例输出
-
Wrong Correct
提示:拓扑排序
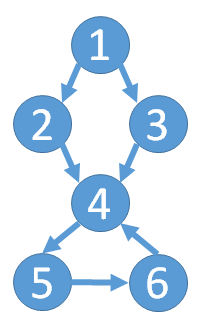
小Ho拿出纸笔边画边说道:如果把每一门课程看作一个点,那么顺序关系也就是一条有向边了。错误的情况也就是出现了环。我知道了!这次我们要做的是判定一个有向图是否有环。
小Hi:小Ho你有什么想法么?
<小Ho思考了一会儿>
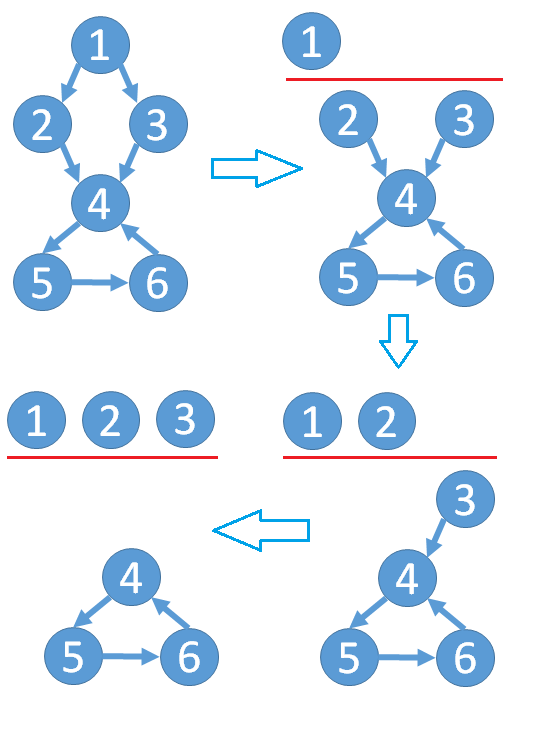
小Ho:一个直观的算法就是每次删除一个入度为0的点,直到没有入度为0的点为止。如果这时还有点没被删除,这些没被删除的点至少组成一个环;反之如果所有点都被删除了,则有向图中一定没有环。
小Hi:Good Job!那赶快去写代码吧!
小Ho又思考了一会儿,挠了挠头说:每次删除一个点之后都要找出当前入度为0的点,这一步我没想到高效的方法。通过扫描一遍剩余的边可以找所有出当前入度为0的点,但是每次删除一个节点之后都扫描一遍的话复杂度很高。
小Hi赞许道:看来你已经养成写代码前分析复杂度的意识了!这里确实需要一些实现技巧,才能把复杂度降为O(N+M),其中N和M分别代表点数和边数。我给你一个提示:如果我们能维护每个点的入度值,也就是在删除点的同时更新受影响的点的入度值,那么是不是就能快速找出入度为0的点了呢?
小Ho:我明白了,这个问题可以这样来解决:
1. 计算每一个点的入度值deg[i],这一步需要扫描所有点和边,复杂度O(N+M)。
2. 把入度为0的点加入队列Q中,当然有可能存在多个入度为0的点,同时它们之间也不会存在连接关系,所以按照任意顺序加入Q都是可以的。
3. 从Q中取出一个点p。对于每一个未删除且与p相连的点q,deg[q] = deg[q] - 1;如果deg[q]==0,把q加入Q。
4. 不断重复第3步,直到Q为空。
最后剩下的未被删除的点,也就是组成环的点了。
小Hi:没错。这一过程就叫做拓扑排序。
小Ho:我懂了。我这就去实现它!
< 十分钟之后 >
小Ho:小Hi,不好了,我的程序写好之后编译就出诡异错误了!
小Hi:诡异错误?让我看看。
小Hi凑近电脑屏幕看了看小Ho的源代码,只见小Ho写了如下的代码:
int edge[ MAXN ][ MAXN ];
小Hi:小Ho,你有理解这题的数据范围么?
小Ho:N最大等于10万啊,怎么了?
小Hi:你的数组有10万乘上10万,也就是100亿了。算上一个int为4个字节,这也得400亿字节,将近40G了呢。
小Ho:啊?!那我应该怎么?QAQ
小Hi:这里就教你一个小技巧好了:
这道题目中N的数据范围在10万,若采用邻接矩阵的方式来储存数据显然是会内存溢出。而且每次枚举一个点时也可能会因为枚举过多无用的而导致超时。因此在这道题目中我们需要采用邻接表的方式来储存我们的数据:
常见的邻接表大多是使用的指针来进行元素的串联,其实我们可以通过数组来模拟这一过程。
int head[ MAXN + 1] = {0}; // 表示头指针,初始化为0 int p[ MAXM + 1]; // 表示指向的节点 int next[ MAXM + 1] = {0}; // 模拟指针,初始化为0 int edgecnt; // 记录边的数量 void addedge(int u, int v) { // 添加边(u,v) ++edgecnt; p[ edgecnt ] = v; next[ edgecnt ] = head[u]; head[u] = edgecnt; } // 枚举边的过程,u为起始点 for (int i = head[u]; i; i = next[i]) { v = p[i]; ... }小Ho:原来还有这种办法啊?好咧。我这就去改进我的算法=v=
 View Code
View Code1 #include <iostream> 2 #include <queue> 3 #include <vector> 4 using namespace std; 5 6 bool isTuopu(vector<vector<int> >& Graph) //拓扑排序 7 { 8 queue<int> Hq; //记录入度为0的结点 9 vector<int> rudu(Graph.size(), 0); //记录结点的入度 10 for(int i=0; i<Graph.size(); i++) 11 { 12 for (int j=0; j<Graph[i].size(); j++) 13 { 14 rudu[Graph[i][j]]++; 15 } 16 17 } 18 19 for (int i=0; i<rudu.size(); i++) 20 { 21 if(rudu[i]==0) 22 Hq.push(i); 23 } 24 25 if(Hq.empty()) 26 return false; 27 28 while(!Hq.empty()) 29 { 30 int tmp = Hq.front(); 31 Hq.pop(); 32 for(int i=0; i<Graph[tmp].size(); i++) 33 { 34 rudu[ Graph[tmp][i] ]--; 35 if( rudu[ Graph[tmp][i] ]==0 ) 36 Hq.push(Graph[tmp][i]); 37 } 38 } 39 40 for(int i=0; i<rudu.size(); i++) 41 if(rudu[i]!=0) 42 return false; 43 return true; 44 } 45 46 int main() 47 { 48 vector<int> edge; 49 //vector<vector<int> > Graph(100000, edge); 50 51 vector<bool> res; 52 53 int T, N, M; 54 cin>>T; 55 while(T--) 56 { 57 cin>>N>>M; 58 vector<vector<int> > Graph(N, edge); //边表 59 60 while(M--) 61 { 62 int a, b; 63 cin>>a>>b; 64 a--; //顶点数从0开始 65 b--; 66 Graph[a].push_back(b); 67 } 68 res.push_back(isTuopu(Graph)); 69 } 70 71 for (int i=0; i<res.size(); i++) 72 { 73 if(res[i]) 74 cout<<"Correct"<<endl; 75 else 76 cout<<"Wrong"<<endl; 77 } 78 79 return 0; 80 81 }
