uva 1411 Ants

题意：

一个平面上有n个黑色的点，n个白色的点，要求黑色的点与白色点之间一一配对，且线段之间不相交。

思路：

线段不相交并不好处理，想了很久想不出，所以看了蓝书的讲解。

一个很明显的结论是，不相交的线段一定比相交的线段短，如图：一个较为直观的例子。

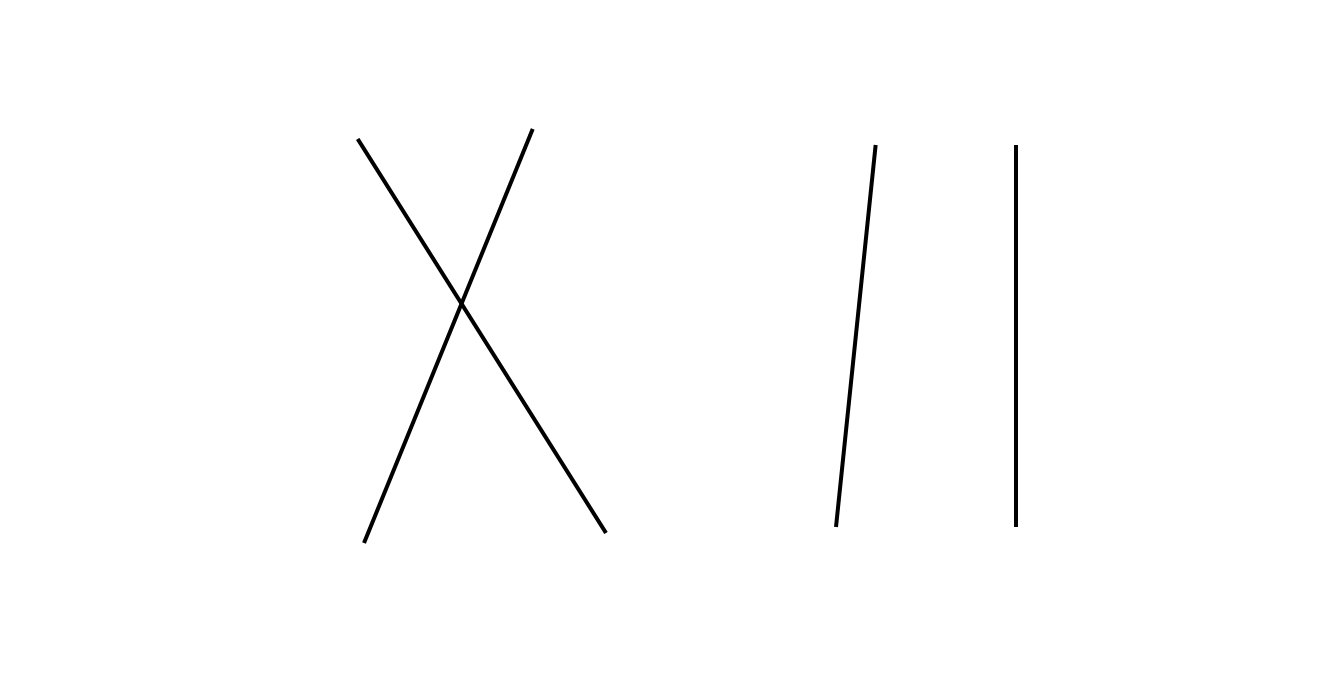
由于点之间一一对应，所以肯定用二分图匹配，然后要使得所有线段之和最短，那么就是求一个带权最小匹配，上KM算法解决。

把所有的边权取负值，求最大匹配即可。

代码：

#include <stdio.h>
#include <math.h>
#include <string.h>
#include <algorithm>
#include <vector>
using namespace std;

const int N = 105;

double mp[N][N];

struct node
{
    double x,y;
    node(double a,double b)
    {
        x = a;
        y = b;
    }
};

vector<node> nx,ny;

bool vis_x[N],vis_y[N];
int match[N];
double lx[N],ly[N];
double slack[N];
int ma[N];

double cal(int i,int j)
{
    double dx = pow(nx[i].x - ny[j].x,2);
    double dy = pow(nx[i].y - ny[j].y,2);
    
    return sqrt(dx + dy);
}

bool dfs(int u,int n)
{
    vis_x[u] = 1;
    
    for (int i = 0;i < n;i++)
    {
        if (vis_y[i]) continue;
        
        double gap = lx[u] + ly[i] - mp[u][i];
        
        //getchar();
        
        //printf("%.6f %.6f %.6f %.6f
",lx[u],ly[i],mp[u][i],gap);
        
        if (fabs(gap) < 1e-6)
        {
            vis_y[i] = 1;
            
            if (match[i] == -1 || dfs(match[i],n))
            {
                match[i] = u;
                return true;
            }
        } 
        else
        {
            slack[i] = min(slack[i],gap);
        }
    }
    
    return false;
}

void km(int n)
{
    memset(ly,0,sizeof(ly));
    memset(match,-1,sizeof(match));
    
    for (int i = 0;i < n;i++)
    {
        lx[i] = mp[i][0];
        
        for (int j = 1;j < n;j++)
        {
            lx[i] = max(lx[i],mp[i][j]);
        }
    }
    
    for (int i = 0;i < n;i++)
    {
        for (int j = 0;j < n;j++) slack[j] = 1e15;
        //printf("gg");
        while (1)
        {
            //printf("233");
            memset(vis_x,0,sizeof(vis_x));
            memset(vis_y,0,sizeof(vis_y));
            
            if (dfs(i,n)) break;
            
            double d = 1e15;
            
            for (int j = 0;j < n;j++)
            {
                if (!vis_y[j]) d = min(slack[j],d);
            }
            
            for (int j = 0;j < n;j++)
            {
                if (vis_x[j]) lx[j] -= d;
                
                if (vis_y[j]) ly[j] += d;
            }
            
            //getchar();
            
            //printf("%.6f **
",d);
        }
    }
}

int main()
{
    int n;
    int kase = 0;
    
    while (scanf("%d",&n) != EOF)
    {
        if (kase++) printf("
");
        
        nx.clear();
        ny.clear();
        
        for (int i = 0;i < n;i++)
        {
            double x,y;
            scanf("%lf%lf",&x,&y);
            
            nx.push_back(node(x,y));
        }
        
        for (int i = 0;i < n;i++)
        {
            double x,y;
            scanf("%lf%lf",&x,&y);
            
            ny.push_back(node(x,y));
        }
        
        for (int i = 0;i < n;i++)
        {
            for (int j = 0;j < n;j++)
            {
                mp[i][j] = -cal(i,j);
            }
        }
        
        km(n);
        
        for (int i = 0;i < n;i++)
        {
            int a = i + 1,b = match[i] + 1;
            ma[b] = a;
        }
        
        for (int i = 0;i < n;i++)
        {
            printf("%d
",ma[i+1]);
        }
    }
    
    return 0;
}