深度学习在设计神经网络结构时需要指定每个隐藏层权重矩阵、偏置项的维度,有的时候容易搞混淆,导致运行时产生维度不对的错误,特别是对于隐藏层既深又宽的网络,更容易出错。下面以一个实例来说明怎么简单快速确定每一层各个矩阵的维度。
假设需要拟合的函数为:y=f(x)=WX+b。
损失函数:J(W,b)
其中 X:输入特征,W:权重,b:偏置项
正(前)向传播的计算公式
a[0]=X,z[i]=w[i]*a[i-1]+b[i] ,a[i]=g[i](z[i])
向量化表示
A[0]=X,Z[i]=W[i]*A[i-1]+b[i] ,A[i]=g[i](Z[i])
反(后)向传播的计算公式
dz[i]=da[i]*g[i](z[i]),dw[i]=dz[i]*a[i-1]
db[i]=dz[i],da[i-1]=w[i].T*dz[i]
向量化表示
dZ[i]=dA[i]*g[i](Z[i]),dW[i]=1/m*dZ[i]*A[i-1].T
db[i]=1/m*np.sum(dZ[i],axis=1,keepdims=True)
dA[i-1]=W[i].T*dZ[i],W[i]=W[i-1]-α*dJ(W,b)
对上述公式的简要说明
i:第i层(从1开始计数)
X:输入特征
g[i]:第i层使用的激活函数
A[i]:第i层的输出(也是第i+1层的输入)
m:样本数量
dZ[i]:偏导数,dW[i]:偏导数,db[i]:偏导数,dA[i-1]:偏导数,dJ(W,b):偏导数
α:学习率
神经网络示例
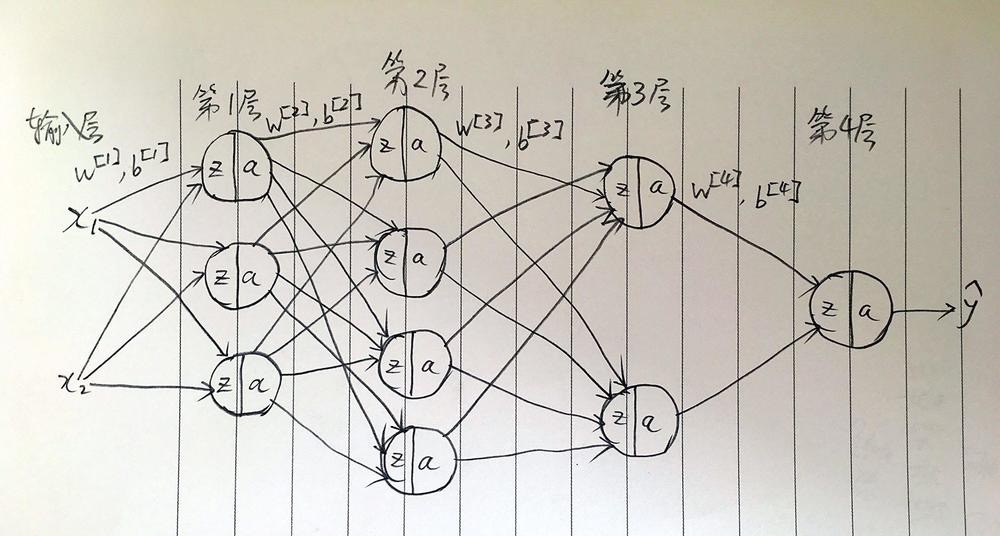
上图中每个圆圈表示一个神经元。
n[i]:第i层的神经元数量,i=0时表示输入层的特征数目(上图中有x1,x2两个特征),m:样本数量。
计算矩阵的维度
w[i]=[n[i], n[i-1]],维度是:n[i]行,n[i-1]列。从图中可知行数是本层神经元的数量,列数是前一层神经元的数量。
b[i]=[n[i], 1],维度是:n[i]行,1列
a[i]=z[i]=[n[i], 1],维度是:n[i]行,1列。由前面的正向传播公式:a[i]=g[i](z[i]),可知a与z的维度是相同的。
a[0]:输入层,a[i] :第 i+1 层的输入
由上面的规则可知示例神经网络图中,w[1]是一个3行2列的矩阵,b[1]是3行1列的矩阵,a[1]和z[1]也是3行1列的矩阵,由此类推:w[2]是一个4行3列的矩阵,w[3]是一个2行4列的矩阵,w[4]是一个1行2列的矩阵。
简单总结
对于w矩阵,行数:本层神经元的数量,列数:前一层神经元的数量(第0层即是输入层特征的数量)
对于b矩阵,行数:该层w矩阵的行数,列数:1
对于z和a矩阵,行数:该层w矩阵的行数,列数:1
在确定了各层矩阵之后,神经网络就设计好了,下一个环节就是设计算法步骤训练模型。模型训练过程中需要根据训练情况调适模型,使得模型对训练数据及测试数据的拟合度高、误差小,训练模型时尤其需要注意偏差与方差问题,参看 深度学习模型训练之偏差与方差。