python大战机器学习——聚类和EM算法

　　注：本文中涉及到的公式一律省略（公式不好敲出来），若想了解公式的具体实现，请参考原著。

1、基本概念

　　（1）聚类的思想：

　　　　将数据集划分为若干个不想交的子集（称为一个簇cluster），每个簇潜在地对应于某一个概念。但是每个簇所具有现实意义由使用者自己决定，聚类算法仅仅会进行划分。

　　（2）聚类的作用：

　　　　1）可以作为一个单独的过程，用于寻找数据的一个分布规律

　　　　2）作为分类的预处理过程。首先对分类数据进行聚类处理，然后在聚类结果的每一个簇上执行分类过程。

　　（3）聚类的性能度量：

　　　　1）外部指标：该指标是由聚类结果与某个参考模型进行比较而获得的。这些外部指标性能度量的结果都在[0,1]之间，这些值越大，说明聚类的性能越好。

　　　　　　Jaccard系数：它刻画了所有属于同一类的样本对同时在C和C*中隶属于同一类的样本对的概率  JC=a/(a+b+c)

　　　　　　FM指数：它刻画了在C中属于同一类的样本对中，同时属于C*的样本对的比例为p1；在C*中属于同一类的样本对中，同时属于C的样本对比例为p2,FMI              　就是p1和p2的几何平均  FMI=sqrt((a/(a+b))*(a/(a+c)))

　　　　　　Rand指数：它刻画的是同时隶属于C，C*的样本对于既不隶属于C，又不隶属于C*的样本对之和占所有样本对的比例  RI=2*（a+d）/(N*(N-1))

　　　　　　ARI指数：对于随机聚类，RI指数不保证接近0。而ARI指数就可通过利用个随机聚类情况下的RI（即E[RI]）来解决这个问题。

　　　　2）内部指标：该指标直接由考察聚类结果而得到的，并不利用任何参考模型

　　　　　　DB指数：它刻画的是，给定两个簇，每个簇样本之间平均值之和比上两个簇的中心点之间的距离作为作为度量。然后考察该度量对所有簇的平均值。显                 然DBI越小越好。如果每个簇样本之间的平均值越小（即簇内样本距离都很近），则DBI越小；如果簇间中心点的距离越大（即簇间样本距离相互越远），则                 DBI越小

　　　　　　Dunn指数：它刻画的是任意两个簇之间最近的距离的最小值，除以任意一个簇内距离最远的两个点的距离的最大值。DI越大越好。　　　　　　

 　　（4）距离度量：

　　　　1）闵可夫斯基距离 

　　　　2）VDM距离：它刻画的是属性取值在各簇上的频率分布之间的差异（当属性取值为非数值类时）

　　通过高斯分布，随机生成聚类簇的样本数据，代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
from sklearn import mixture

def create_data(centers,num=100,std=0.7):
    X,labels_true=make_blobs(n_samples=num,centers=centers,cluster_std=std)
    return X,labels_true

def plot_data(*data):
    X,labels_true=data
    labels=np.unique(labels_true) #the diffrent cluster(K numbers)
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    colors='rgbyckm'
    for i,label in enumerate(labels):
        position=labels_true==label
        ax.scatter(X[position,0],X[position,1],label="cluster %d"%label,color=colors[i%len(colors)])

    ax.legend(loc="best",framealpha=0.5)
    ax.set_xlabel("X[0]")
    ax.set_ylabel("Y[1]")
    ax.set_title("data")
    plt.show()

X,labels_true=create_data([[1,1],[2,2],[1,2],[10,20]],1000,0.5)
plot_data(X,labels_true)

　　结果如下：

2、k均值算法

　　输入：样本集D，聚类簇数K

　　输出：簇划分C

　　算法步骤：

　　　　1）从D中随机选择K个样本作为初始簇均值向量u

　　　　2）重复迭代直到算法收敛（迭代内容参考书中内容）

　　注：K均值算法总能够收敛，但是其收敛情况高度依赖于初始化的均值，有可能收敛到局部极小值。因此通常都是用多组初始均值向量来计算若干次，选择其中最优的一次。而k-means++策略选择的初始均值向量可以在一定程度上解决这个问题。

　　实验代码一：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
from sklearn import mixture

def create_data(centers,num=100,std=0.7):
    X,labels_true=make_blobs(n_samples=num,centers=centers,cluster_std=std)
    return X,labels_true

def test_Kmeans(*data):
    X,labels_true=data
    clst=cluster.KMeans()
    clst.fit(X)
    predicted_labels=clst.predict(X)
    print("ARI:%s"%adjusted_rand_score(labels_true,predicted_labels))
    print("Sum center distance %s"%clst.inertia_)

def plot_data(*data):
    X,labels_true=data
    labels=np.unique(labels_true) #the diffrent cluster(K numbers)
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    colors='rgbyckm'
    for i,label in enumerate(labels):
        position=labels_true==label
        ax.scatter(X[position,0],X[position,1],label="cluster %d"%label,color=colors[i%len(colors)])

    ax.legend(loc="best",framealpha=0.5)
    ax.set_xlabel("X[0]")
    ax.set_ylabel("Y[1]")
    ax.set_title("data")
    plt.show()

X,labels_true=create_data([[1,1],[2,2],[1,2],[10,20]],1000,0.5)
#plot_data(X,labels_true)
test_Kmeans(X,labels_true)

　　实验结果一：

　　其中ARI指标越大越好

　　实验代码二：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
from sklearn import mixture

def create_data(centers,num=100,std=0.7):
    X,labels_true=make_blobs(n_samples=num,centers=centers,cluster_std=std)
    return X,labels_true

def test_Kmeans_nclusters(*data):
    X,labels_true=data
    nums=range(1,50)
    ARIs=[]
    Distances=[]
    for num in nums:
        clst=cluster.KMeans(n_clusters=num)
        clst.fit(X)
        predicted_labels=clst.predict(X)
        ARIs.append(adjusted_rand_score(labels_true,predicted_labels))
        Distances.append(clst.inertia_)
    fig = plt.figure()
    ax = fig.add_subplot(1, 2, 1)
    ax.plot(nums,ARIs,marker="+")
    ax.set_xlabel("n_clusters")
    ax.set_ylabel("ARI")
    ax=fig.add_subplot(1,2,2)
    ax.plot(nums,Distances,marker='o')
    ax.set_xlabel("n_clusters")
    ax.set_ylabel("inertia_")
    fig.suptitle("KMeans")
    plt.show()

X,labels_true=create_data([[1,1],[2,2],[1,2],[10,20]],1000,0.5)
#plot_data(X,labels_true)
#test_Kmeans(X,labels_true)
test_Kmeans_nclusters(X,labels_true)

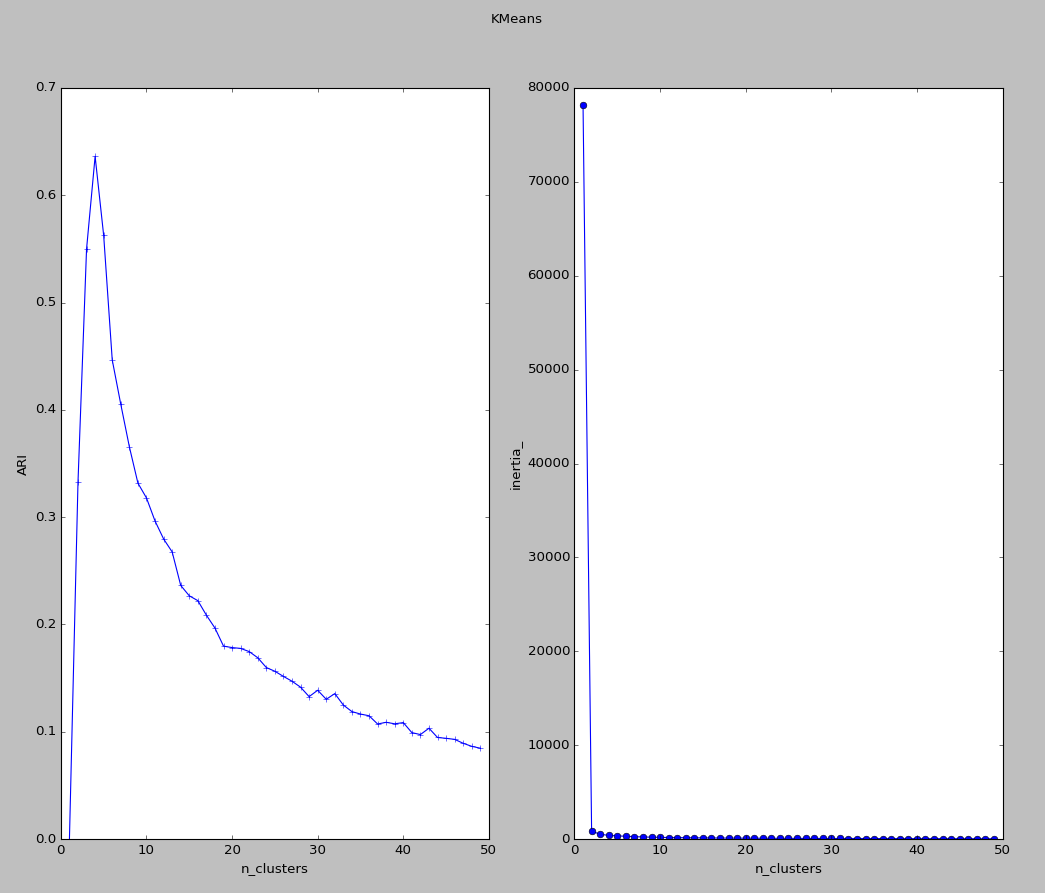
　　实验结果二：

　　该结果显示了聚类簇的数目对ARI和inertial_的影响

3、高斯混合聚类

　　其通过概率模型来表示聚类原型。若已知高斯混合分布，则高斯混合聚类的原理是：如果样本xi最优可能是Z=k产生的，则可将该样本划归到簇Ck。即通过最大后验概率确定样本所属的聚类。现在的问题是，如何学习高斯混合分布的参数。由于涉及隐变量Z，故可以采用EM算法求解。

　　输入：观察数据D，高斯混合成分个数K

　　输出：高斯混合模型参数

　　算法步骤：

　　　　1）取参数的初始值

　　　　2）迭代直至算法收敛。迭代过程如下：

　　　　　　E步：根据当前模型参数，计算分模型k对观测数据xj的响应度：Υjk

　　　　　　M步：计算新一轮迭代的模型参数：uk<i+1>,Σk<i+1>，αk<i+1>

　　实验代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
from sklearn import mixture

def create_data(centers,num=100,std=0.7):
    X,labels_true=make_blobs(n_samples=num,centers=centers,cluster_std=std)
    return X,labels_true

def test_GMM_n_componets(*data):
    X,labels_true=data
    nums=range(1,50)
    ARIs=[]
    for num in nums:
        clst=mixture.GMM(n_components=num)
        predicted_labels=clst.fit_predict(X)
        ARIs.append(adjusted_rand_score(labels_true,predicted_labels))
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.plot(nums,ARIs,marker='+',color='r')
    ax.set_xlabel("n_componnents")
    ax.set_ylabel("ARI")
    fig.suptitle("GMM")
    plt.show()

centers=[[1,1],[2,2],[1,2],[10,20]]
X,labels_true=create_data(centers,1000,0.5)
test_GMM_n_componets(X,labels_true)

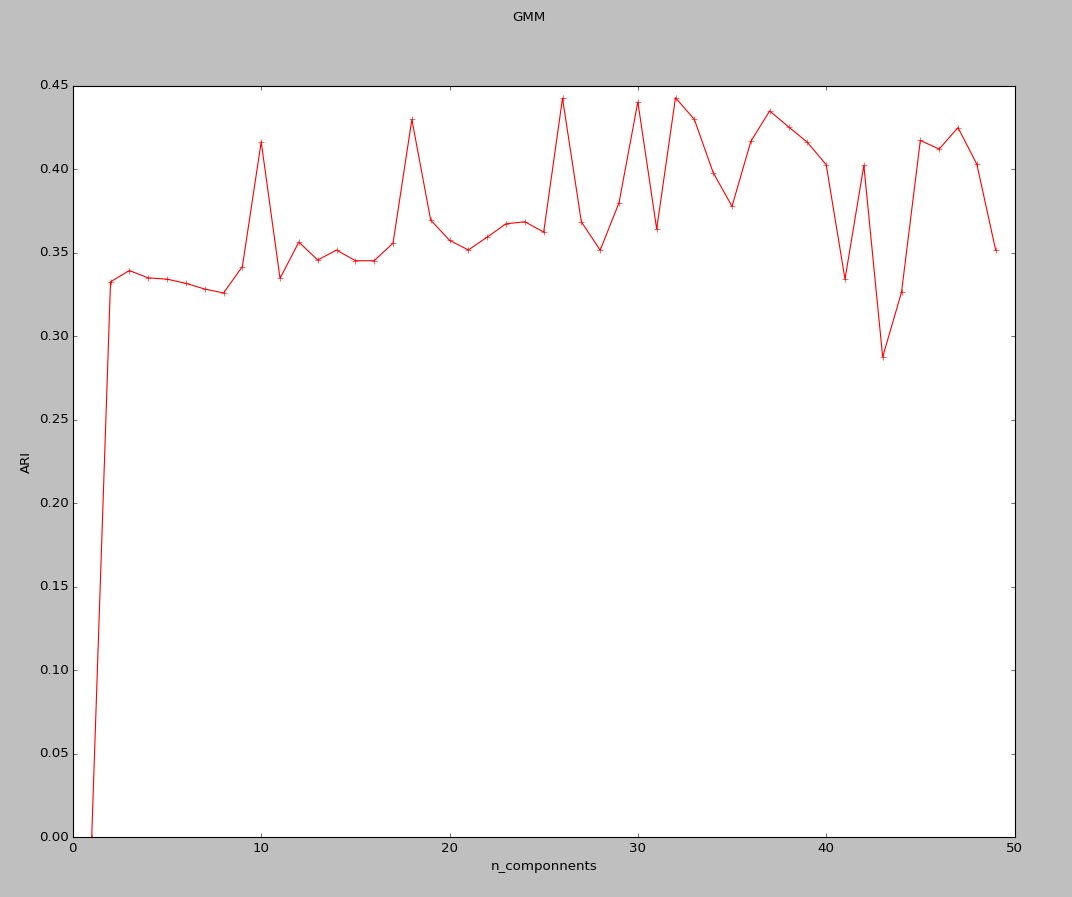
　　实验结果：

　　奇怪的是这里所得到的结果与所想并不一致，和书中给的结果也不相同，但不知道原因在哪。

4、密度聚类

　　其假设聚类结构能够通过样本分布的紧密程度来确定。DBSCAN是常用的密度聚类算法

　　DBSCAN算法的定义：给定领域参数（ε，MinPts），一个簇C∈D是满足下列性质的非空样本子集：1）最大连接性  2）最大性     即一个簇是由密度可达关系导出的最大的密度相连样本集合

　　DBSCAN算法的思想：若x为核心对象，则x密度可达的所有样本组成的集合记作X，可以证明X就是满足连接性与最大性的簇。

 　　输入：数据集D，领域参数（ε，MinPts）

　　输出：簇划分C

　　算法步骤：

　　　　1）初始化核心对象集合为空集

　　　　2）寻找核心对象

　　　　3）迭代：以任一未访问过的核心对象为出发点，找出有密度可达的样本生成的聚类簇，直到所有核心对象都被访问为止

　　实验代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
from sklearn import mixture

def create_data(centers,num=100,std=0.7):
    X,labels_true=make_blobs(n_samples=num,centers=centers,cluster_std=std)
    return X,labels_true

def test_DBSCAN(*data):
    X,labels_true=data
    clst=cluster.DBSCAN()
    predicted_labels=clst.fit_predict(X)
    print("ARI:%s"%adjusted_rand_score(labels_true,predicted_labels))
    print("Core sample num:%d"%len(clst.core_sample_indices_))


X,labels_true=create_data([[1,1],[2,2],[1,2],[10,20]],1000,0.5)
test_DBSCAN(X,labels_true)

　　实验结果：

5、层次聚类

　　其可在不用层上对数据集进行划分，形成树状的聚类结构。AGNES是一种常用的层次聚类算法

　　AGNES算法原理：AGNES首先将数据集中的每个样本看作一个初始的聚类簇，然后再不断地找出距离最近的两个聚类簇进行合并。就这样不断地合并直到达到预设的聚类簇的个数。

　　依据选择不同的距离计算方式，算法名不同。

　　输入：数据集D，聚类簇距离度量函数d，聚类簇数量K

　　输出：簇划分C

　　算法步骤：

　　　　1）初始化：每个样本都作为一个簇

　　　　2）迭代：终止条件为聚类簇的数量K（计算聚类簇之间的距离，找出距离最近的两个簇，将这两个簇合并）

　　代码如下：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score
from sklearn import mixture

def create_data(centers,num=100,std=0.7):
    X,labels_true=make_blobs(n_samples=num,centers=centers,cluster_std=std)
    return X,labels_true

def test_AgglomerativeClustering(*data):
    X,labels_true=data
    nums=range(1,50)
    linkages=['ward','complete','average']
    markers="+o*"
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)

    for i,linkage in enumerate(linkages):

        ARIs=[]
        for num in nums:
            clst=cluster.AgglomerativeClustering(n_clusters=num,linkage=linkage)
            predicted_labels=clst.fit_predict(X)
            ARIs.append(adjusted_rand_score(labels_true,predicted_labels))
        ax.plot(nums,ARIs,marker=markers[i],label="linkage=%s"%linkage)

    ax.set_xlabel("n_clusters")
    ax.set_ylabel("ARI")
    ax.legend(loc="best")
    fig.suptitle("AgglomerativeClustering")
    plt.show()

centers=[[1,1],[2,2],[1,2],[10,20]]
X,labels_true=create_data(centers,1000,0.5)
test_AgglomerativeClustering(X,labels_true)

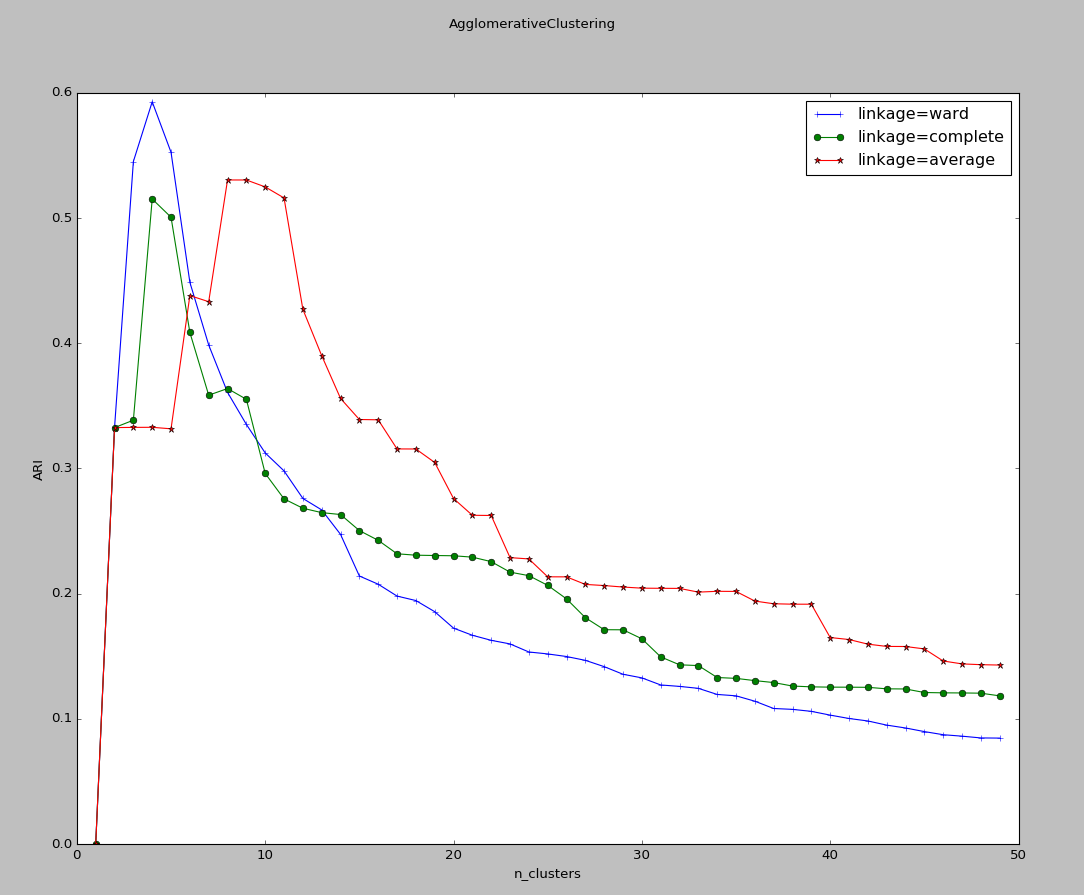
　　实验结果：

　　可以看到，三种链接方式随分类簇的数量的总体趋势相差无几。但是单链接方式ward的峰值最大，且峰值最大的分类簇的数量刚好等于实际上生成样本的簇的数量

6、EM算法

　　也称为期望极大算法，它是一种迭代算法，用于含有隐变量的概率模型参数估计。

　　输入：观测变量数据Y，隐变量数据Z，联合分布P（Y，Z；θ），条件分布P（Z|Y；θ）　　　　

　　输出：模型参数θ

　　算法步骤：

　　　　1）选择参数的初值θ0

　　　　2）反复迭代直到收敛

　　注：1）EM算法的收敛性蕴含了两层意义：对数似然函数序列L（θi）收敛；参数估计序列θi收敛。前者并不蕴含后者。

　　　　2）EM算法的初值的选择非常重要，常用的办法是给出一批初值，然后分别从每个初值开始使用EM算法。最后对得到的各个估计值加以比较，从中选择对数似然函数最大的那个。

7、实际中的聚类要求

　　（1）可伸缩性

　　（2）不同类型属性的处理能力

　　（3）发现任意形状的类簇

　　（4）初始化参数

　　（5）算法的抗噪能力

　　（6）增量聚类和对输入次序的敏感度

　　（7）高维处理能力

　　（8）结果的可解释性和可用性

8、各种聚类算法的使用情况对比

模型	关键参数	使用场景
K均值算法	簇的数量	通用聚类方法，用于均匀的簇的大小，簇的数量 不多的情况
DBSCAN	ε，MinPts	用于不均匀的簇大小，以及非平坦的集合结构
AgglometativeClustering算法	簇的数量，链接类型	用于簇的数量较多，有链接约束等情况
GMM算法	一些	用于平坦的集合结构，对密度估计很合适

　　在实际应用中，聚类簇的数量的选取通常结合性能度量指标和具体问题分析。