博弈论入门

巴什博弈

今天打比赛的时候做到的，下来去看了一些资料，感觉蛮有意思的（学好了可以用来坑钱）

两个顶尖聪明的人在玩游戏，有n个石子，每人可以随便拿1−m个石子，不能拿的人为败者，问谁会胜利。

当石子有1−m个时，毫无疑问，先手必胜。

当石子有m+1个时，先手无论拿几个，后手都可以拿干净，先手必败。

当石子有m+2−2m时，先手可以拿走几个，剩下m+1个，先手必胜。

我们不难发现，面临m+1个石子的人一定失败。

这样的话两个人的最优策略一定是通过拿走石子，使得对方拿石子时还有m+1个。

推广：

• 设当前的石子数为n=k∗(m+1)+r
  

先手会首先拿走r个，接下来假设后手拿走x个，先手会拿走m+1−x个，这样博弈下去后手最终一定失败。

• 设当前的石子数为n=k∗(m+1)
  

假设先手拿xx个，后手一定会拿m+1−x个，这样下去先手一定失败。

放题：

https://ac.nowcoder.com/acm/contest/11746/D

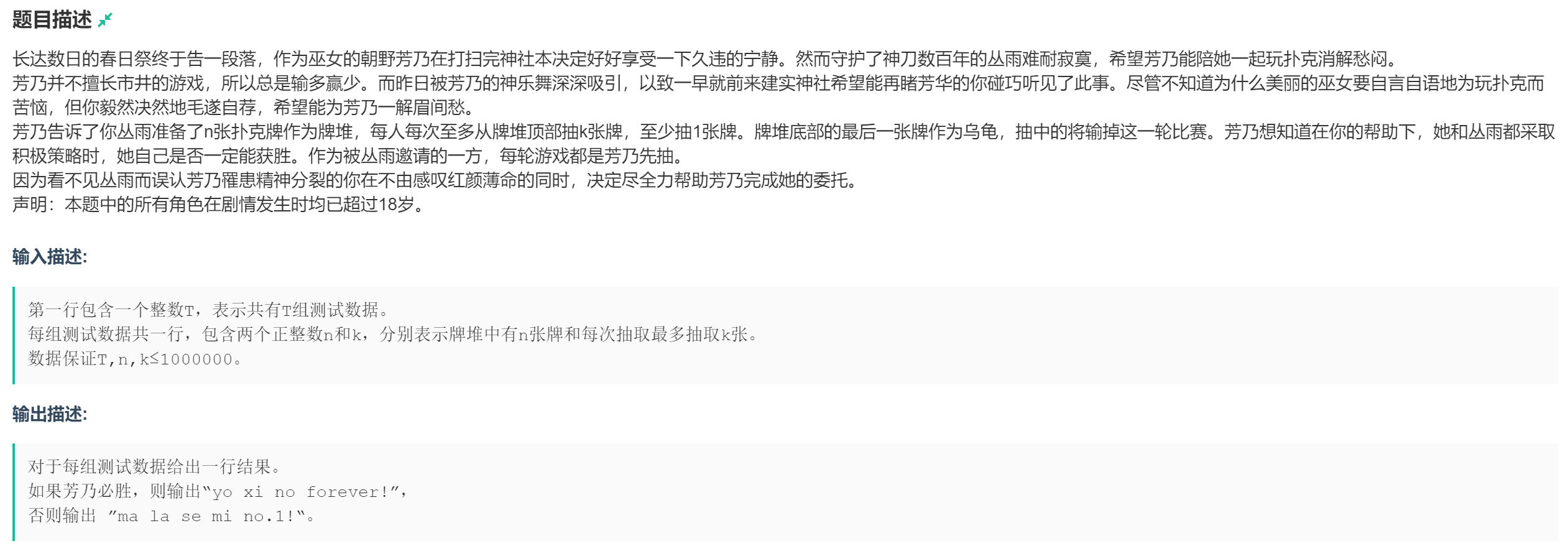
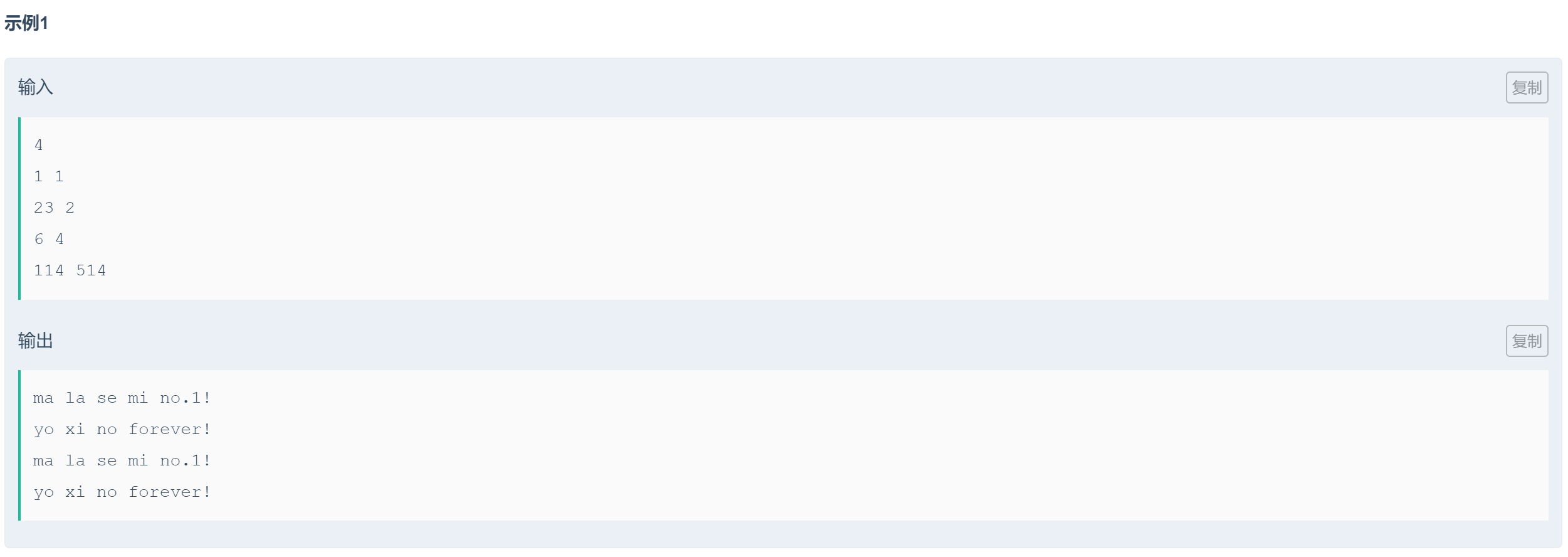
这里是摸到最后一张牌的人为输。

假设k=3，那么后手就能把石子数控制为4，也就是k+1，这时一共是n-1张牌，留下的一张就是输家摸的。如果n-1张牌能整除4的话，最后一张牌就会是先手摸，这时先手输，否则后手输，只要让对方面对的牌数为k+1的倍数+1，自己就能赢。

这道题需要特殊考虑一下n=1和k>n-1时的情况。

代码如下：

#include<stdio.h>
int main()
{
    int t,n,k;
    scanf("%d",&t);
    for(int i=0;i<t;i++){
        scanf("%d%d",&n,&k);
        if(n==1)
        printf("ma la se mi no.1!
");
        else if(k>n-1)
        printf("yo xi no forever!
");
        else if((n-1)%(k+1)==0)
        printf("ma la se mi no.1!
");
        else
        printf("yo xi no forever!
");
    }
    return 0;
}

（参考博客：https://www.cnblogs.com/zwfymqz/p/8460192.html）

EOF