Lesson17——NumPy 统计函数

NumPy 教程目录

^{1 NumPy 统计函数}

　　NumPy 提供了很多统计函数，用于从数组中查找最小元素，最大元素，百分位标准差和方差等。 函数说明如下

1.1 统计

method	description
amin(a[, axis, out, keepdims, initial, where])	返回数组的最小值或沿轴的最小值。
amax(a[, axis, out, keepdims, initial, where])	返回数组的最大值或沿轴的最大值。
nanmin(a[, axis, out, keepdims])	返回数组的最小值或沿轴的最小值，忽略任何 NaN。
nanmax(a[, axis, out, keepdims])	返回数组的最大值或沿轴的最大值，忽略任何 NaN。
ptp(a[, axis, out, keepdims])	沿轴的值范围（最大值 - 最小值）。
percentile(a, q[, axis, out, …])	沿指定轴计算数据的第 q 个百分位数。
nanpercentile(a, q[, axis, out, …])	计算沿指定轴的数据的第 q 个百分位数，同时忽略 nan 值。
quantile(a, q[, axis, out, overwrite_input, …])	沿指定轴计算数据的第 q 个分位数。
nanquantile(a, q[, axis, out, …])	沿指定轴计算数据的第 q 个分位数，同时忽略 nan 值。

1.2 平均值和方差

method	description
median(a[, axis, out, overwrite_input, keepdims])	计算沿指定轴的中位数。
average(a[, axis, weights, returned])	计算沿指定轴的加权平均值。
mean(a[, axis, dtype, out, keepdims])	计算沿指定轴的算术平均值。
std(a[, axis, dtype, out, ddof, keepdims])	计算沿指定轴的标准差。
var(a[, axis, dtype, out, ddof, keepdims])	计算沿指定轴的方差。
nanmedian(a[, axis, out, overwrite_input, …])	计算沿指定轴的中位数，同时忽略 NaN。
nanmean(a[, axis, dtype, out, keepdims])	计算沿指定轴的算术平均值，忽略 NaN。
nanstd(a[, axis, dtype, out, ddof, keepdims])	计算沿指定轴的标准差，同时忽略 NaN。
nanvar(a[, axis, dtype, out, ddof, keepdims])	计算沿指定轴的方差，同时忽略 NaN。

1.3 相关系数

method	description
corrcoef(x[, y, rowvar, bias, ddof])	返回 Pearson 积矩相关系数。
correlate(a, v[, mode])	两个一维序列的互相关。
cov(m[, y, rowvar, bias, ddof, fweights, …])	给定数据和权重，估计协方差矩阵。

1.4 直方图

method	description
histogram(a[, bins, range, normed, weights, …])	计算一组数据的直方图。
histogram2d(x, y[, bins, range, normed, …])	计算两个数据样本的二维直方图。
histogramdd(sample[, bins, range, normed, …])	计算一些数据的多维直方图。
bincount(x[, weights, minlength])	计算非负整数数组中每个值的出现次数。
histogram_bin_edges(a[, bins, range, weights])	仅计算直方图函数使用的 bin 边缘的函数。
digitize(x, bins[, right])	返回输入数组中每个值所属的 bin 的索引。

2 统计例子

2.1 numpy.amin()

　　numpy.amin() 用于计算数组中的元素沿指定轴的最小值。

Example：

a = np.array([[3,7,5],[8,4,3],[2,4,9]])  
print(a)
print(np.amin(a)) #所有元素的最小值
print(np.amin(a,axis=0)) #每列元素的最小值
print(np.amin(a,axis=1))  #每行元素的最小值
"""
[[3 7 5]
 [8 4 3]
 [2 4 9]]
 
2

[2 4 3]

[3 3 2]
"""

2.2 numpy.amax()

　　numpy.amax() 用于计算数组中的元素沿指定轴的最大值。

Example：

a = np.array([[3,7,5],[8,4,3],[2,4,9]])  
print(a)
print(np.amax(a)) #所有元素的最大值
print(np.amax(a,axis=0)) #每列元素的最大值
print(np.amax(a,axis=1))  #每行元素的最大值
"""
[[3 7 5]
 [8 4 3]
 [2 4 9]]
9
[8 7 9]
[7 8 9]
"""

2.3 numpy.nanmin()

　　numpy.nanmin(a, axis=None, out=None, keepdims=<no value>, initial=<no value>, where=<no value>)  返回数组的最小值或沿轴的最小值，忽略任何 NaN。 当遇到所有 NaN 切片时，会引发 RuntimeWarning 并为该切片返回 Nan。

Example：

a = np.array([[1, 2], [3, np.nan],[3, -np.nan]])
print(np.amin(a))
print(np.nanmin(a))
print(np.nanmin(a,axis=0))
print(np.nanmin(a,axis=1))
"""
nan
1.0
[1. 2.]
[1. 3. 3.]
"""

2.4 numpy.nanmax()

　　numpy.nanmax(a, axis=None, out=None, keepdims=<no value>, initial=<no value>, where=<no value>) 返回数组的最大值或沿轴的最大值，忽略任何 NaN。 当遇到所有 NaN 切片时，会引发 RuntimeWarning 并为该切片返回 NaN。

Example：

a = np.array([[1, 2], [3, np.nan],[3, -np.nan]])
print(np.amax(a))
print(np.nanmax(a))
print(np.nanmax(a,axis=0))
print(np.nanmax(a,axis=1))
"""
nan
3.0
[3. 2.]
[2. 3. 3.]
"""

2.5 numpy.ptp()

　　numpy.ptp(a, axis=None, out=None, keepdims=<no value>) 沿轴的值范围（最大值 - 最小值）。

Example：

x = np.array([[4, 9, 2, 10],
              [6, 9, 7, 12]])
print(np.ptp(x))
print(np.ptp(x,axis=0))
print(np.ptp(x,axis=1))
"""
10
[2 0 5 2]
[8 6]
"""

2.6 numpy.percentile()

　　numpy.percentile(a, q, axis=None, out=None, overwrite_input=False, method='linear', keepdims=False, *, interpolation=None) 百分位数是统计中使用的度量，表示小于这个值的观察值的百分比。

　　参数说明：

• • a： 输入数组
  • q：要计算的百分位数，在 0 ~ 100 之间
  • axis: 沿着它计算百分位数的轴

　　首先明确百分位数：

　　第 $q$ 个百分位数是这样一个值，它使得至少有 q% 的数据项小于或等于这个值，且至少有 (100-q)% 的数据项大于或等于这个值。

举个例子：高等院校的入学考试成绩经常以百分位数的形式报告。比如，假设某个考生在入学考试中的语文部分的原始分数为 54 分。相对于参加同一考试的其他学生来说，他的成绩如何并不容易知道。但是如果原始分数54分恰好对应的是第70百分位数，我们就能知道大约70%的学生的考分比他低，而约30%的学生考分比他高。

Example：

a = np.array([[10, 7, 4], [3, 2, 1]])
print ('我们的数组是：')
print (a)
print ('调用 percentile() 函数：')
# 50% 的分位数，就是 a 里排序之后的中位数
print (np.percentile(a, 50)) 
# axis 为 0，在纵列上求
print (np.percentile(a, 50, axis=0)) 
# axis 为 1，在横行上求
print (np.percentile(a, 50, axis=1)) 
# 保持维度不变
print (np.percentile(a, 50, axis=1, keepdims=True))
"""
我们的数组是：
[[10  7  4]
 [ 3  2  1]]
调用 percentile() 函数：
3.5
[6.5 4.5 2.5]
[7. 2.]
[[7.]
 [2.]]
"""

2.7 numpy.quantile()

　　numpy.quantile(a, q, axis=None, out=None, overwrite_input=False, method='linear', keepdims=False, *, interpolation=None) 沿指定轴计算数据的第 q 个分位数。

Note

　　给定长度为 N 的向量V，V的第 q 个分位数是从最小到最大的方式的值 q 如果归一化排名与 q 的位置完全不匹配，则两个最近邻居的值和距离以及内插参数将确定分位数。如果 q = 0.5，此函数与中位数相同；如果 q = 0.0，此函数与最小值相同；如果 q = 1.0，则与最大值相同.

Example：

>>> a = np.array([[10, 7, 4], [3, 2, 1]])
>>> a
array([[10,  7,  4],
       [ 3,  2,  1]])
>>> np.quantile(a, 0.5)
3.5
>>> np.quantile(a, 0.5, axis=0)
array([6.5, 4.5, 2.5])
>>> np.quantile(a, 0.5, axis=1)
array([7.,  2.])
>>> np.quantile(a, 0.5, axis=1, keepdims=True)
array([[7.],
       [2.]])
>>> m = np.quantile(a, 0.5, axis=0)
>>> out = np.zeros_like(m)
>>> np.quantile(a, 0.5, axis=0, out=out)
array([6.5, 4.5, 2.5])
>>> m
array([6.5, 4.5, 2.5])
>>> b = a.copy()
>>> np.quantile(b, 0.5, axis=1, overwrite_input=True)
array([7.,  2.])
>>> assert not np.all(a == b)

3 平均值和方差

3.1 numpy.median()

　　numpy.median(a, axis=None, out=None, overwrite_input=False, keepdims=False) 计算沿指定轴的中位数。

Example：

a = np.array([[10, 7, 4], [3, 2, 1]])
print(a)
print(np.median(a))  #所有元素的中位数
print(np.median(a, axis=0))
print(np.median(a, axis=1))
"""
[[10  7  4]
 [ 3  2  1]]
3.5
[6.5 4.5 2.5]
[7.,  2.]
"""

Example：

m = np.median(a, axis=0)
out = np.zeros_like(m)
print(np.median(a, axis=0, out=m))
print(m)
b = a.copy()
print(np.median(b, axis=1, overwrite_input=True))
assert not np.all(a==b)
b = a.copy()
print(np.median(b, axis=None, overwrite_input=True))
assert not np.all(a==b)
"""
[6.5 4.5 2.5]
[6.5 4.5 2.5]
[7. 2.]
3.5
"""

3.2 numpy.average()

　　numpy.average(a, axis=None, weights=None, returned=False) 计算沿指定轴的加权平均值。

　　计算方式为：avg = sum(a * weights) / sum(weights)

Example：

data = np.arange(1, 5)
print(data)
print(np.average(data))
print(np.average(np.arange(1, 11), weights=np.arange(10, 0, -1)))
"""
[1 2 3 4]
2.5
4.0
"""

Example：

data = np.arange(6).reshape((3,2))
print(data)
print(np.average(data, axis=1, weights=[1./4, 3./4]))
"""
[[0 1]
 [2 3]
 [4 5]]
[0.75 2.75 4.75]
"""

3.3 numpy.mean()

　　numpy.mean(a, axis=None, dtype=None, out=None, keepdims=<no value>, *, where=<no value>) 计算沿指定轴的算术平均值。

Example：

a = np.array([[1, 2], [3, 4]])
print(np.mean(a))
print(np.mean(a, axis=0))
print(np.mean(a, axis=1))
"""
2.5
[2. 3.]
[1.5 3.5]
"""

3.4 numpy.std()

　　numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>, *, where=<no value>) 计算沿指定轴的标准差。

Example：

a = np.array([[1, 2], [3, 4]])
print( np.std(a))
print(np.std(a, axis=0))
print(np.std(a, axis=1))
"""
1.118033988749895
[1. 1.]
[0.5 0.5]
"""

3.5 numpy.var()

　　numpy.var(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>, *, where=<no value>) 计算沿指定轴的方差。

Example：

a = np.array([[1, 2], [3, 4]])
print( np.var(a))
print(np.var(a, axis=0))
print(np.var(a, axis=1))
"""
1.25
[1. 1.]
[0.25 0.25]
"""

4 相关系数

4.1 numpy.corrcoef()

　　numpy.corrcoef(x, y=None, rowvar=True, bias=<no value>, ddof=<no value>, *, dtype=None) 返回 Pearson 积矩相关系数。

Example：

rng = np.random.default_rng(seed=42)
xarr = rng.random((3, 3))
print(xarr)
"""
[[0.77395605 0.43887844 0.85859792]
 [0.69736803 0.09417735 0.97562235]
 [0.7611397  0.78606431 0.12811363]]
"""
R1 = np.corrcoef(xarr)
print(R1)
"""
[[ 1.          0.99256089 -0.68080986]
 [ 0.99256089  1.         -0.76492172]
 [-0.68080986 -0.76492172  1.        ]]
"""

4.2 numpy.correlate()

　　numpy.correlate(a, v, mode='valid') 两个一维序列的互相关。

Example：

print(np.correlate([1, 2, 3], [0, 1, 0.5]))
print(np.correlate([1, 2, 3], [0, 1, 0.5], "same"))
print(np.correlate([1, 2, 3], [0, 1, 0.5], "full"))
"""
[3.5]
[2.  3.5 3. ]
[0.5 2.  3.5 3.  0. ]
"""

4.3 numpy.cov()

　　numpy.cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None, aweights=None, *, dtype=None) 给定数据和权重，估计协方差矩阵。

Example：

m = np.arange(10, dtype=np.float64)
f = np.arange(10) * 2
a = np.arange(10) ** 2.
ddof = 1
w = f * a
v1 = np.sum(w)
v2 = np.sum(w * a)
m -= np.sum(m * w, axis=None, keepdims=True) / v1
cov = np.dot(m * w, m.T) * v1 / (v1**2 - ddof * v2)
print(cov)
"""
2.368621947484198
"""

Example：

x = np.array([[0, 2], [1, 1], [2, 0]]).T
print(x)
print(np.cov(x))
"""
[[0 1 2]
 [2 1 0]]
[[ 1. -1.]
 [-1.  1.]]
"""

5 直方图

5.1 numpy.histogram()

　　numpy.histogram(a, bins=10, range=None, normed=None, weights=None, density=None) 计算数据集的直方图。

Example：

print( np.histogram([1, 2, 1], bins=[0, 1, 2, 3]))
print( np.histogram(np.arange(4), bins=np.arange(5), density=True))
print( np.histogram([[1, 2, 1], [1, 0, 1]], bins=[0,1,2,3]))
"""
(array([0, 2, 1], dtype=int64), array([0, 1, 2, 3]))
(array([0.25, 0.25, 0.25, 0.25]), array([0, 1, 2, 3, 4]))
(array([1, 4, 1], dtype=int64), array([0, 1, 2, 3]))
"""

Example：

a = np.arange(5)
hist, bin_edges = np.histogram(a, density=True)
print(hist)
print(hist.sum())
print(np.sum(hist * np.diff(bin_edges)))
"""
[0.5 0.  0.5 0.  0.  0.5 0.  0.5 0.  0.5]
2.4999999999999996
1.0
"""

Example：

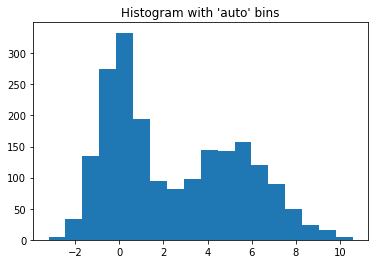
rng = np.random.RandomState(10)  # deterministic random data
a = np.hstack((rng.normal(size=1000),
               rng.normal(loc=5, scale=2, size=1000)))
_ = plt.hist(a, bins='auto')  # arguments are passed to np.histogram
plt.title("Histogram with 'auto' bins")
Text(0.5, 1.0, "Histogram with 'auto' bins")
plt.show()

输出结果：