论文信息
论文标题:Attention-driven Graph Clustering Network
论文作者:Zhihao Peng, Hui Liu, Yuheng Jia, Junhui Hou
论文来源:2021, ACM Multimedia
论文地址:download
论文代码:download
1 Introduction
研究现状:使用自动编码器提取节点属性特征,利用图卷积网络捕获拓扑图特征。
缺点如下:
-
- 没有一种灵活的机制融合 AE 和 GCN 产生的特征表示。[ 说白了就是实验效果不好 ]
- 忽略不同层 embedding 的多尺度信息,进行后续的聚类分配导致聚类结果较差。[ 本文的一个优势 ]
AGCN 包括了两个 融合 模块
-
- AGCN heterogeneity-wise fusion module (
AGCN-H):AGCN-H 自适应地合并了来自同一层的 GCN 特征和 AE 特征。 - AGCN scale-wise fusion module (
AGCN-S):AGCN-S 动态地连接了来自不同层的多尺度特征。
- AGCN heterogeneity-wise fusion module (
上述两个模块都是基于注意力机制 ,动态度量相应特征对后续特征融合的重要性。
定义如 Table 1 所示:
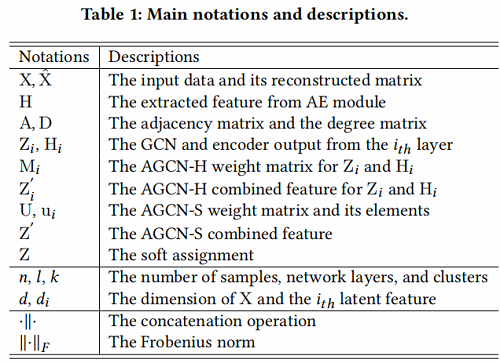
2 Method
本章节,先介绍 AGCN-H 和 AGCN-S ,然后介绍训练过程。
AGCN 架构如下:
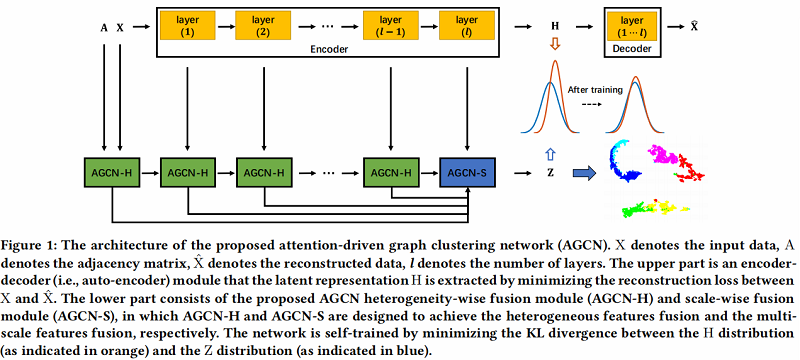
具体的两个模块:
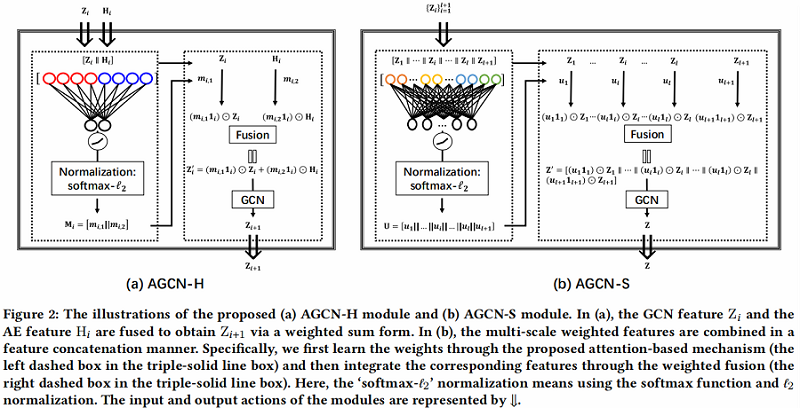
2.1 AGCN-H
AGCN-H 自适应地合并了来自同一层的 GCN 特征和 AE 特征。通过注意力系数学习,随后进行加权特征融合。
AGCN-H 的对应说明如 Figure 2(a) 所示,实现细节如下:
Step1:利用自编码器提取潜在表示,重构损失如下:
$\begin{array}{l}\mathcal{L}_{R}=\|\mathrm{X}-\hat{\mathrm{X}}\|_{F}^{2} \\\text { s.t. } \quad\left\{\mathrm{H}_{i}=\phi\left(\mathrm{W}_{i}^{\mathrm{e}} \mathrm{H}_{i-1}+\mathrm{b}_{i}^{\mathrm{e}}\right)\right. \\\left.\hat{\mathrm{H}}_{i}=\phi\left(\mathrm{W}_{i}^{d} \hat{\mathrm{H}}_{i-1}+\mathrm{b}_{i}^{d}\right), i=1, \cdots, l\right\}\end{array}\quad \quad \quad (1)$

class AE(nn.Module):
def __init__(self, n_enc_1, n_enc_2, n_enc_3, n_dec_1, n_dec_2, n_dec_3,
n_input, n_z):
super(AE, self).__init__()
# encoder
self.enc_1 = Linear(n_input, n_enc_1)
self.enc_2 = Linear(n_enc_1, n_enc_2)
self.enc_3 = Linear(n_enc_2, n_enc_3)
# extracted feature by AE
self.z_layer = Linear(n_enc_3, n_z)
# decoder
self.dec_1 = Linear(n_z, n_dec_1)
self.dec_2 = Linear(n_dec_1, n_dec_2)
self.dec_3 = Linear(n_dec_2, n_dec_3)
self.x_bar_layer = Linear(n_dec_3, n_input)
def forward(self, x):
enc_z2 = F.relu(self.enc_1(x))
enc_z3 = F.relu(self.enc_2(enc_z2))
enc_z4 = F.relu(self.enc_3(enc_z3))
z = self.z_layer(enc_z4)
dec_z2 = F.relu(self.dec_1(z))
dec_z3 = F.relu(self.dec_2(dec_z2))
dec_z4 = F.relu(self.dec_3(dec_z3))
x_bar = self.x_bar_layer(dec_z4)
return x_bar, enc_z2, enc_z3, enc_z4, z
Step2:学习相应的注意力系数
- 将 $\mathrm{Z}_{i}$ 和 $\mathrm{H}_{i}$ 先进行拼接,
- 将上述拼接的 $ \left[\mathrm{Z}_{i} \| \mathrm{H}_{i}\right] \in \mathbb{R}^{n \times 2 d_{i}}$ ,进行全连接操作;
- 将上述结果使用激活函数 LeakyReLU ;
- 最后再使用 softmax function 和 $\ell_{2}$ normalization;
Step2 可以公式化为 :
$\mathrm{M}_{i}=\ell_{2}\left(\operatorname{softmax}\left(\left(\text { LeakyReLU }\left(\left[\mathrm{Z}_{i} \| \mathrm{H}_{i}\right] \mathrm{W}_{i}^{a}\right)\right)\right)\right)\quad \quad\quad(2)$
其中:
- $\mathrm{M}_{i}=\left[\mathrm{m}_{i, 1} \| \mathrm{m}_{i, 2}\right] \in \mathbb{R}^{n \times 2}$ 是 attention coefficient matrix ,且 每项大于 0;
- $\mathrm{m}_{i, 1}$,$ \mathrm{~m}_{i, 2}$ 是衡量 $\mathrm{Z}_{i}$、$\mathrm{H}_{i}$ 重要性的权重向量;

m1 = self.mlp1( torch.cat((h1,z1), 1) )
m1 = F.normalize(m1,p=2)
Step 3:融合第 $i$ 层的 GCN 的特征 $Z_{i}$ 和 AE 的特征 $ \mathrm{H}_{i} $ :
$\mathrm{Z}_{i}^{\prime}=\left(\mathrm{m}_{i, 1} 1_{i}\right) \odot \mathrm{Z}_{i}+\left(\mathrm{m}_{i, 2} 1_{i}\right) \odot \mathrm{H}_{i}\quad \quad \quad (3)$
其中:
- $1_{i} \in \mathbb{R}^{1 \times d_{i}}$ 代表着全 $1$ 向量;
- $ '\odot'$ 代表着 Hadamard product ;

m11 = torch.reshape(m1[:,0], [n_x, 1])
m12 = torch.reshape(m1[:,1], [n_x, 1])
m11_broadcast = m11.repeat(1,500)
m12_broadcast = m12.repeat(1,500)
z1_bar = m11_broadcast.mul(z1)+m12_broadcast.mul(h1)
Step 4:将上述生成的 $Z_{i}^{\prime} \in \mathbb{R}^{n \times d_{i}}$ 当作第 $i+1$ 层 GCN 的输入,获得 $\mathrm{Z}_{i+1}$ :
$\mathrm{Z}_{i+1}=\text { LeakyReLU }\left(\mathrm{D}^{-\frac{1}{2}}(\mathrm{~A}+\mathrm{I}) \mathrm{D}^{-\frac{1}{2}} \mathrm{Z}_{i}^{\prime} \mathrm{W}_{i}\right)\quad \quad (4)$
其中
- GCN 原始模型中的邻接矩阵 $A$ 变形为 $ D^{-\frac{1}{2}}(A+ I) \mathrm{D}^{-\frac{1}{2}}$ ;
- $\mathrm{I} \in \mathbb{R}^{n \times n}$ ;

z2 = self.agcn_1( z1_bar, adj)
2.2 AGCN-S
Step1:将 multi-scale features $Z_{i}$ 拼接在一起。
$\mathrm{Z}^{\prime}=\left[\mathrm{Z}_{1}\|\cdots\| \mathrm{Z}_{i}\|\cdots\| \mathrm{Z}_{l} \| \mathrm{Z}_{l+1}\right]\quad\quad \quad (5)$
其中:
- $\mathrm{Z}_{l+1}=\mathrm{H}_{l} \in \mathbb{R}^{n \times d_{l}}$ 表示 $\mathrm{Z}_{l+1}$ 的信息只来自自编码器。
Step2:将上述生成的 $\mathrm{Z}^{\prime}$ 放入全连接网络,并使用 $\text { softmax- } \ell_{2}$ 标准化:
$\mathrm{U}=\ell_{2}\left(\operatorname{softmax}\left(\operatorname{LeakyReLU}\left(\left[\mathrm{Z}_{1}\|\cdots\| \mathrm{Z}_{i}\|\cdots\| \mathrm{Z}_{l} \| \mathrm{Z}_{l+1}\right] \mathrm{W}^{s}\right)\right)\right)\quad \quad\quad(6)$
其中:
- $\mathrm{U}=\left[\mathrm{u}_{1}\|\cdots\| \mathrm{u}_{i}\|\cdots\| \mathrm{u}_{l} \| \mathrm{u}_{l+1}\right] \in \mathbb{R}^{n \times(l+1)}$ 且每个数大于 $0$ ;
- $u_{i}$ 代表了 $\mathrm{Z}_{i}$ 的 parallel attention coefficient ;

u = self.mlp(torch.cat((z1,z2,z3,z4,z),1))
u = F.normalize(u,p=2)
u0 = torch.reshape(u[:,0], [n_x, 1])
u1 = torch.reshape(u[:,1], [n_x, 1])
u2 = torch.reshape(u[:,2], [n_x, 1])
u3 = torch.reshape(u[:,3], [n_x, 1])
u4 = torch.reshape(u[:,4], [n_x, 1])
Step3:为了进一步探究多尺度特征,考虑在 attention 系数上施加一个相应的权重:
$\mathrm{Z}^{\prime}= {\left[\left(\mathrm{u}_{1} 1_{1}\right) \odot \mathrm{Z}_{1}\|\cdots\|\left(\mathrm{u}_{i} 1_{i}\right) \odot \mathrm{Z}_{i}\|\cdots\|\left(\mathrm{u}_{l} 1_{l}\right) \odot \mathrm{Z}_{l} \|\right.} \left.\left(\mathrm{u}_{l+1} 1_{l+1}\right) \odot \mathrm{Z}_{l+1}\right]\quad \quad \quad (7)$

tile_u0 = u0.repeat(1,500)
tile_u1 = u1.repeat(1,500)
tile_u2 = u2.repeat(1,2000)
tile_u3 = u3.repeat(1,10)
tile_u4 = u4.repeat(1,10)
net_output = torch.cat((tile_u0.mul(z1), tile_u1.mul(z2), tile_u2.mul(z3), tile_u3.mul(z4), tile_u4.mul(z)), 1 )
Step4 :$ Z^{\prime}$ 将作为最终预测的输入,预测输出为 $Z \in \mathbb{R}^{n \times k} $ ,其中 $k$ 代表聚类数。
$\begin{array}{l}\mathrm{Z}=\operatorname{softmax}\left(\mathrm{D}^{-\frac{1}{2}}(\mathrm{~A}+\mathrm{I}) \mathrm{D}^{-\frac{1}{2}} \mathrm{Z}^{\prime} \mathrm{W}\right) \\\text { s.t. } \quad \sum_{j=1}^{k} z_{i, j}=1, z_{i, j}>0\end{array}\quad \quad\quad (8)$
预测输出计算:
$\begin{array}{l} y_{i}=\underset{j}{\arg \max }\;\;\; \mathrm{z}_{i, j} \\ \text { s.t. } \quad j=1, \cdots, k \end{array}\quad\quad\quad (9)$

net_output = self.agcn_z(net_output, adj, active=False)
2.3 Training process
训练过程包括两个步骤:
Step 1:
使用 Student's t-distribution 作为核来度量 embedded point 和质心之间的相似度:
${\large q_{i, j}=\frac{\left(1+\left\|\mathrm{h}_{i}-\mu_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}{\sum_{j}\left(1+\left\|\mathrm{h}_{i}-\mu_{j}\right\|^{2} / \alpha\right)^{-\frac{\alpha+1}{2}}}}\quad\quad\quad(10) $
辅助目标分布 $P$:
${\large p_{i, j}=\frac{q_{i, j}^{2} / \sum_{i} q_{i, j}}{\sum_{j}^{\prime} q_{i, j}^{2} / \sum_{i} q_{i, j}}} \quad\quad\quad(11)$
Step 2 :
通过辅助目标分布 $P$ 最小化组合特征分布 $Z$ 和自编码器特征分布 $H$ 的 KL 散度。
$\begin{aligned}\mathcal{L}_{K L} &=\lambda_{1} * K L(\mathrm{P}, \mathrm{Z})+\lambda_{2} * K L(\mathrm{P}, \mathrm{H}) \\&=\lambda_{1} \sum\limits _{i} \sum\limits_{j} p_{i, j} \log \frac{p_{i, j}}{z_{i, j}}+\lambda_{2} \sum\limits_{i} \sum\limits_{j} p_{i, j} \log \frac{p_{i, j}}{q_{i, j}}\end{aligned}\quad\quad\quad(12)$
其中:
-
- $\lambda_{1}>0$ 和 $\lambda_{2}>0$ 是 trade-off parameters ;
联合 Eq.1 和 Eq.12 得到总损失为:
$\mathcal{L}=\mathcal{L}_{R}+\mathcal{L}_{K L}\quad\quad\quad(13)$
AGCN 的训练过程如 Algorithm 1 所示:

3 Experiments
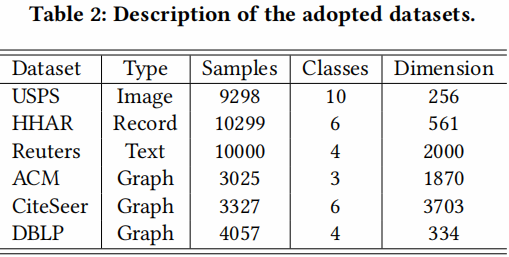
数据集
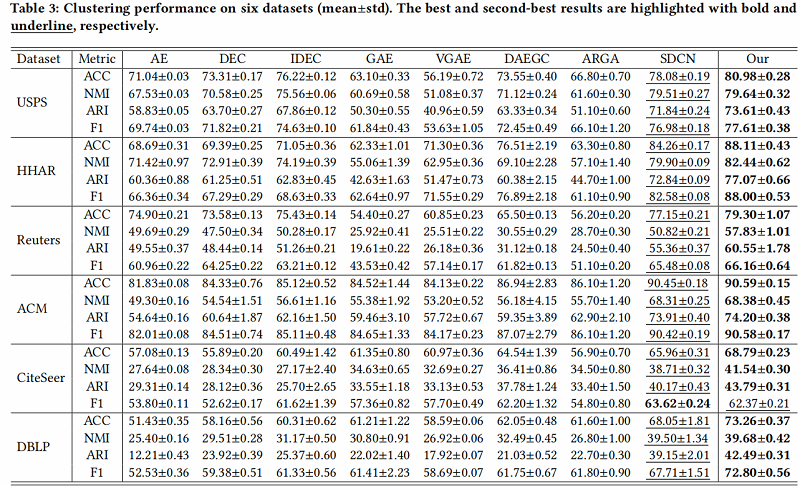
聚类结果
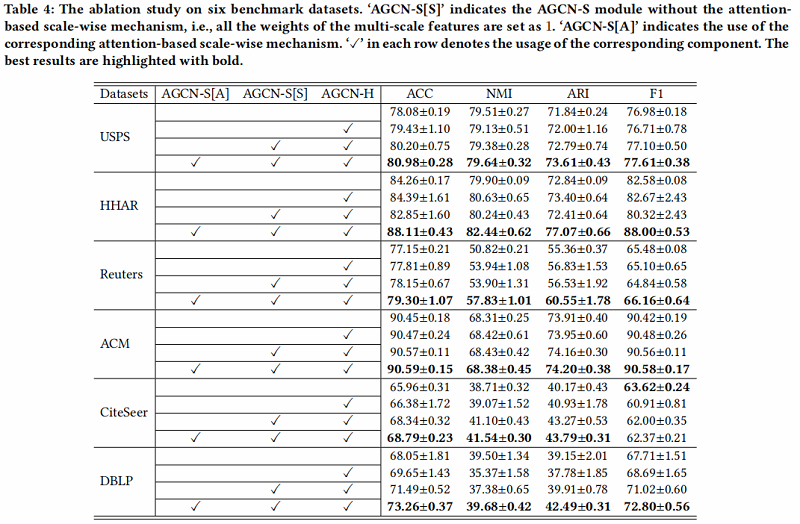
消融实验
进行消融研究,以评估 AGCN-H 模块和 AGCN-S 模块的效率和有效性。此外,我们还分析了不同尺度特征对聚类性能的影响。结果如 Table 4 所示:
- Analysis of AGCN-H module
我们可以观察到,AGCN-H 模块在一定程度上提高了性能 【相较于没有使用】。
- Analysis of AGCN-S module
从两个方面评价 AGCN-S module:
- the multi-scale feature fusion (marked as AGCN-S[S]) ;
- the attention-based scale-wise strategy (marked as AGCN-S[A]) ;
在第一个方面,通过比较表4中每个数据集的第二行和第三行的实验结果,我们可以发现,在大多数情况下,多尺度特征融合可以帮助获得更好的聚类性能。唯一的例外是HHAR,其中间层的一些特征受到过度平滑的问题,导致负传播。
对于第二个方面,通过比较表4中第三行和第四行的每个数据集的结果,我们可以发现,考虑基于注意力的规模级策略能够获得最好的聚类性能。特别是在HHAR数据集中,考虑基于注意力的规模级策略可以充分应对上述性能下降的问题。这一现象被认为是由于基于注意力的尺度策略可以分配一些权值较小的负特征,避免了负传播。这曾经验证了基于注意力的机制的有效性。
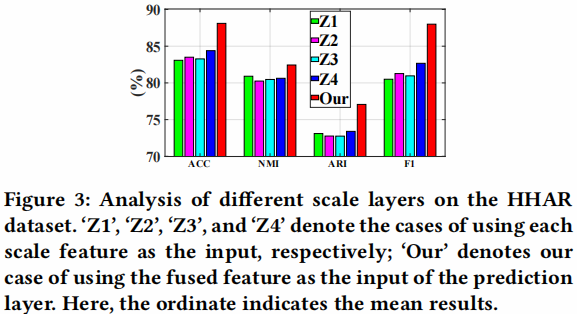
多尺度特征分析
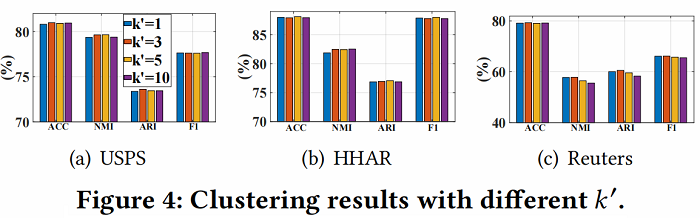
邻居数量 ′ 实验
由于邻域 ‘ 的数量显著影响邻接矩阵的质量,我们对非图数据集,即USPS、HHAR和路透社进行了 ’ 的参数分析。从 Figure 4 中,我们可以观察到我们的模型对 ‘ 不敏感。
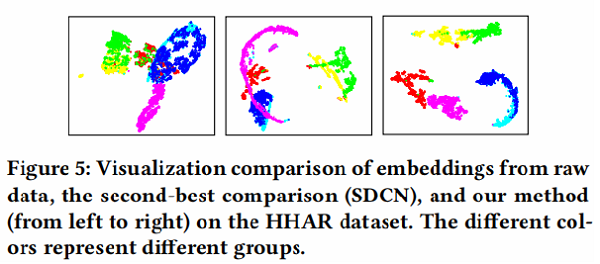
可视化
为了直观地验证我们的方法的有效性,我们绘制了我们方法的学习表示的二维t分布随机邻域嵌入(t-SNE) 可视化,以及图5中HHAR数据集上比较最好的[24]可视化。我们可以发现,通过我们的方法获得的特征表示对不同的簇具有最好的可分性,其中来自同一类的样本自然地聚集在一起,不同组之间的差距是最明显的一个。这一现象证实了,与最先进的方法相比,我们的方法产生了最有区别的表示。
4 Conclusion
在本文中,我们提出了一种新的深度聚类方法,即注意驱动图聚类网络(AGCN),它同时考虑了动态融合策略和多尺度特征融合。通过利用两个新的基于注意力的融合模块,AGCN能够自适应地学习权重的异质性,以实现这些特征融合。此外,在常用的基准数据集上进行的大量实验,验证了所提出的网络优于最先进的方法,特别是对于低质量的图。
修改历史
2022-02-17 创建文章
2022-06-09 修订文章
