注:本文使用的网课资源为中国大学MOOC
https://www.icourse163.org/course/ZJU-93001
最短路径问题
问题抽象
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径
- 这条路径就是两点之间的最短路径(shortest path)
- 第一个顶点为源点(source)
- 最后一个顶点为终点(destination)
问题分类
1、单源最短路径问题,从某固定源点除法,求其到所有其他顶点的最短路径
- (有向)无权图
- (有向)有权图
2、多源最短路径问题:求任意两顶点之间的最短路径
无权图的单源最短路算法
按照递增(或者非递减)的顺序找到各个顶点的最短路(BFS),时间复杂度T=O(|V|+|E|)
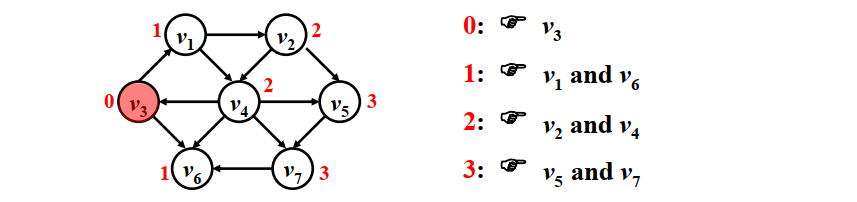
如上图所示,源点为v3,因此第0步从v3开始,其邻接点为v1和v6,入队后分别遍历,此时第1步指向v1和v6;先看v1的邻接点,有v2和v4,再看v6,没有邻接点,因此第2步指向v2和v4;入队后分别遍历,v2的邻接点为v4和v5,因为v4已经被访问,因此v4的下一步只有v5,同理v4的下一步只有v7,因此第3步指向v5和v7,此时图的结点已经全部遍历完。
经过遍历后,dist和path的值分别为:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 1 | 2 | 0 | 2 | 3 | 1 | 3 |
| path | 3 | 1 | -1 | 1 | 2 | 3 | 4 |
/* 邻接表存储 - 无权图的单源最短路算法 */
/* dist[]和path[]全部初始化为-1 */
/* dist用于存放源点到该顶点的最短距离,path存放遍历途中经过的顶点*/
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{
Queue Q;
Vertex V;
PtrToAdjVNode W;
Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */
dist[S] = 0; /* 初始化源点 */
AddQ (Q, S);
while( !IsEmpty(Q) )
{
V = DeleteQ(Q);
for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( dist[W->AdjV]==-1 )
{ /* 若W->AdjV未被访问过 */
dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */
path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */
AddQ(Q, W->AdjV);
}
} /* while结束*/
}
有权图的单源最短路算法(Dijkstra算法)
-
令S={源点s + 已经确定好的最短路径(v_i)}
-
对任一未收录的顶点v,定义dist[v]为s到v的最短路径长度,但该路径仅进过S中的顶点,即路径{$ s o (v_i in S) o v$}的最小长度。
-
若路径是按照递增(非递减)的顺序生成的,则:
- 真正的最短路径必须只经过s中的顶点;
- 每次从未收录的顶点中选一个dist最小的收录
- 每增加一个v进入s,可能影响另一个w的dist值(dist[w] = min{dist[w], dist[v] + <v,w>的权重})
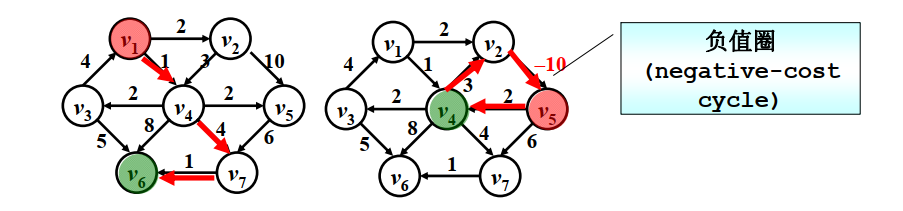
如图所示,不考虑负值圈,设V1为源点,V6为终点,可以找到路径(v_1 o v_4 o v_7 o v_6)是最短路径
遍历前,dist和path的初始值分别为:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | (infty) | (infty) | (infty) | (infty) | (infty) | (infty) | (infty) |
| path | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
- 源点为v1,此时将dist1更新为0, colleted1=true,而v1的邻接点有v2和v4,因此赋值dist2=2,dist4=1,path2=1,path4=1,然后正式进入Dijkstra算法;
- 从未被收录顶点中找dist最小者,此时选择v4: colleted4=true,v4的邻接点有v3,v5,v6,v7。此时赋值dist3=1+2,dist5=1+2,dist6=1+8,dist7=1+4, path3=path5=path6=path7=4;
- 从未被收录顶点中找dist最小者,此时选择v2: colleted2=true, v2的邻接点有v4和v5, 但是v4已被收录,因此只考虑v5, 此时赋值dist5 = min(dist5, 2+10)=3, 则path5仍为4;
- 从未被收录顶点中找dist最小者,因此dist3=dist5=3,此时选择编号较小的v3: colleted3=ture, v3的邻接点有v1和v6, 但是v1已被收录,因此只考虑v6, 此时赋值dist6 = min(dist6, 3+5)=8, 则path6更新为3;
- 从未被收录顶点中找dist最小者,此时选择v5: colleted5=true,v5的邻接点只有v7,此时赋值dist7 = min(dist7, 3+6)=5, 则path7仍为4;
- 从未被收录顶点中找dist最小者,此时选择v7: colleted7=true,v7的邻接点只有v6,此时赋值dist6 = min(dist6, 5+1)=6, 则path6更新为7;
- 从未被收录顶点中找dist最小者,此时选择v6: colleted6=true,由于V6没有邻接点,因此不做操作
- 所有顶点均被收录,退出循环。
经过遍历后,dist和path的值分别为:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| dist | 0 | 2 | 3 | 1 | 3 | 6 | 5 |
| path | -1 | 1 | 4 | 1 | 4 | 7 | 4 |
/* 邻接矩阵存储 - 有权图的单源最短路算法 */
/* 返回未被收录顶点中dist最小者 */
Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{
Vertex MinV, V;
int MinDist = INFINITY;
for (V=0; V<Graph->Nv; V++)
{
if ( collected[V]==false && dist[V]<MinDist)
{
/* 若V未被收录,且dist[V]更小 */
MinDist = dist[V]; /* 更新最小距离 */
MinV = V; /* 更新对应顶点 */
}
}
if (MinDist < INFINITY) /* 若找到最小dist */
return MinV; /* 返回对应的顶点下标 */
else return ERROR; /* 若这样的顶点不存在,返回错误标记 */
}
bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
int collected[MaxVertexNum];
Vertex V, W;
/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */
for ( V=0; V<Graph->Nv; V++ )
{
dist[V] = Graph->G[S][V];
if ( dist[V]<INFINITY )
path[V] = S;
else
path[V] = -1;
collected[V] = false;
}
/* 先将起点收入集合 */
dist[S] = 0;
collected[S] = true;
while (1)
{
/* V = 未被收录顶点中dist最小者 */
V = FindMinDist( Graph, dist, collected );
if ( V==ERROR ) /* 若这样的V不存在 */
break; /* 算法结束 */
collected[V] = true; /* 收录V */
for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
{
/* 若W是V的邻接点并且未被收录 */
if ( collected[W]==false && Graph->G[V][W]<INFINITY )
{
if ( Graph->G[V][W]<0 ) /* 若有负边 */
return false; /* 不能正确解决,返回错误标记 */
/* 若收录V使得dist[W]变小 */
if ( dist[V]+Graph->G[V][W] < dist[W] )
{
dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
path[W] = V; /* 更新S到W的路径 */
}
}
}
} /* while结束*/
return true; // 算法执行完毕,返回正确标记
}
多源最短路算法(FLOYD算法)
-
(D^k[i][j])=路径{(i o l le k o j)}的最小长度
-
(D^0,D^1,...,D^{|V|-1}[i][j])即给出了i到j的真正最短距离
-
最初的(D^{-1})是邻接矩阵,对角元全是0
-
当(D^{k-1})已经完成,递推到(D^k)时:
- 或者(k otin)最短路径{(i o l le k o j)},则(D^k=D^{k-1})
- 或者(kin)最短路径{(i o l le k o j)},则该路径必定由两段最短路径组成(D^k[i][j]=D^{k-1}[i][k]+D^{k-1}[k][j])
/* 邻接矩阵存储 - 多源最短路算法 */
bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{
Vertex i, j, k;
/* 初始化 */
for ( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ )
{
D[i][j] = Graph->G[i][j];
path[i][j] = -1;
}
for( k=0; k<Graph->Nv; k++ )
for( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ )
if( D[i][k] + D[k][j] < D[i][j] )
{
D[i][j] = D[i][k] + D[k][j];
if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */
return false; /* 不能正确解决,返回错误标记 */
path[i][j] = k;
}
return true; /* 算法执行完毕,返回正确标记 */
}
应用实例:哈利波特的考试
题意理解
哈利波特有一门课要考试了,这门课是用魔咒将一种动物变成另一种动物。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe,把猫变成鱼,魔咒lalala。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。
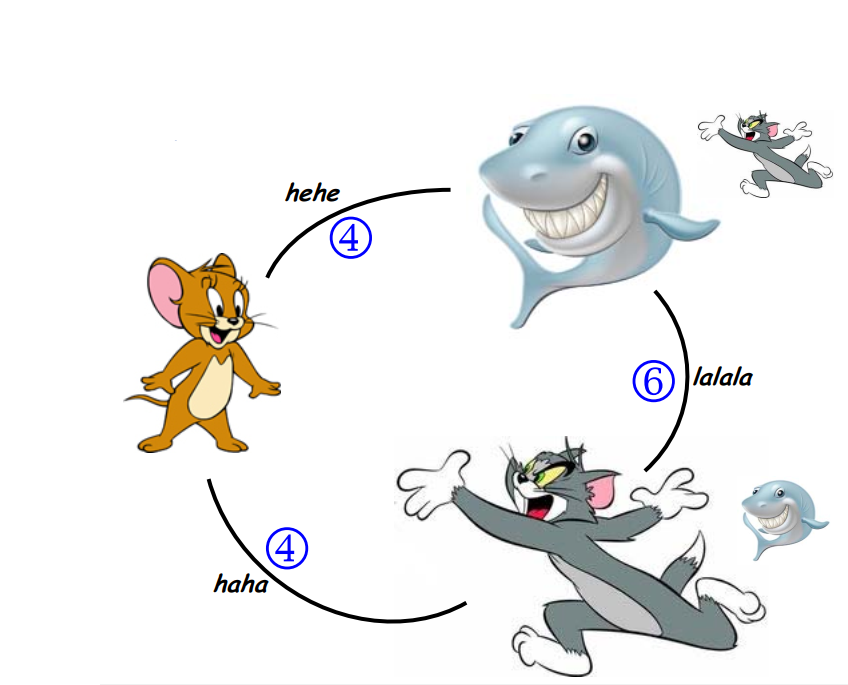
只允许带一只动物,考察把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为自己带去的动物所需要的魔咒最长)需要的魔咒最短?
例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式
第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。
如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
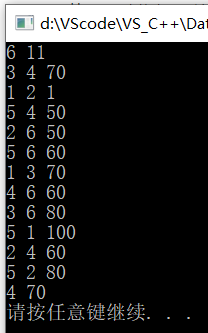
Sample Input
6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80
Sample Output
4 70
解题思路
根据输入样例可以构造图:
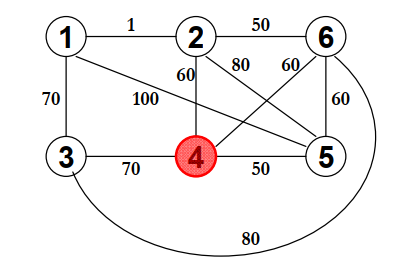
利用Floyd算法,将任意两点之间的最小路径计算出来。对于每一个节点,找出从该节点出发最难变的动物需要多少字符。所有节点最难变的节点的最小值即为所求结果,对应的节点为所求节点。
程序框架
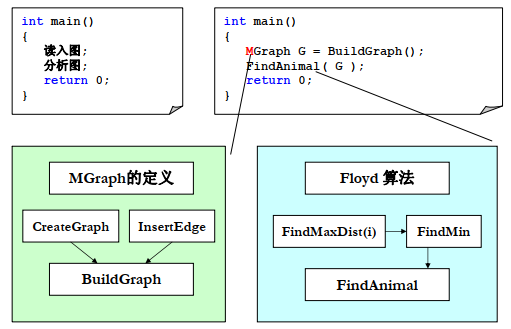
完整代码
#include <iostream>
using namespace std;
#define MaxVertexNum 100 /* 最大顶点数设为100 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型*/
typedef int WeightType; /* 边的权值设为整型*/
//typedef char DataType; /* 顶点存储的数据类型设为字符型*/
/***********全局变量***********/
/* 边的定义*/
typedef struct ENode *PtrToENode;
struct ENode
{
Vertex V1, V2; /* 有向边<V1, V2> */
WeightType Weight; /* 权重*/
};
typedef PtrToENode Edge;
/* 图结点的定义*/
typedef struct GNode *PtrToGNode;
struct GNode
{
int Nv; /* 顶点数*/
int Ne; /* 边数*/
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵*/
// DataType Data[MaxVertexNum]; /* 存顶点的数据*/
/* 注意:很多情况下,顶点无数据,此时Data[]可以不用出现*/
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型*/
/*************函数声明*************/
MGraph CreateGraph(int VertexNum); // 初始化一个有VertexNum个顶点但没有边的图
void InsertEdge(MGraph Graph, Edge E); // 插入边<V1, V2>
MGraph BuildGraph(void); // 根据输入的参数建立图
void Floyd(MGraph Graph, WeightType D[][MaxVertexNum]); // 多源最短路算法
WeightType FindMaxDist(WeightType D[][MaxVertexNum], Vertex i, int N); //找二维数组D中第i行的最大值
void FindAnimal(MGraph Graph); // 找到拥有最短路径的动物编号及其路径长度
/**********************************/
/* 主函数 */
/**********************************/
int main()
{
MGraph G = BuildGraph();
FindAnimal(G);
system("PAUSE");
return 0;
}
/*************函数声明*************/
/* 初始化一个有VertexNum个顶点但没有边的图*/
MGraph CreateGraph(int VertexNum)
{
Vertex V, W;
MGraph Graph;
Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图*/
Graph->Nv = VertexNum;
Graph->Ne = 0;
/* 初始化邻接矩阵*/
/* 注意:这里默认顶点编号从0开始,到(Graph->Nv - 1) */
for (V = 0; V < Graph->Nv; V++)
for (W = 0; W < Graph->Nv; W++)
Graph->G[V][W] = INFINITY;
return Graph;
}
/* 插入边<V1, V2> */
void InsertEdge( MGraph Graph, Edge E )
{
Graph->G[E->V1][E->V2] = E->Weight;
/* 若是无向图,还要插入边<V2, V1> */
Graph->G[E->V2][E->V1] = E->Weight;
}
/* 根据输入的参数建立图 */
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
// Vertex V;
int Nv, i;
cin >> Nv; /* 读入顶点个数*/
Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图*/
cin >> (Graph->Ne); /* 读入边数*/
if (Graph->Ne != 0) /* 如果有边*/
{
E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点*/
/* 读入边,格式为"起点终点权重",插入邻接矩阵*/
for (i = 0; i < Graph->Ne; i++)
{
cin >> (E->V1) >> (E->V2) >> (E->Weight);
/* 注意:如果权重不是整型,Weight的读入格式要改*/
E->V1--;
E->V2--; //起始编号从0开始
InsertEdge(Graph, E);
}
}
/* 如果顶点有数据的话,读入数据
for (V = 0; V<Graph->Nv; V++)
scanf(" %c", &(Graph->Data[V]));
*/
return Graph;
}
/* 多源最短路算法 */
/* 输出各顶点之间的距离矩阵D*/
void Floyd( MGraph Graph, WeightType D[][MaxVertexNum] )
{
Vertex i, j, k;
/* 初始化*/
for (i = 0; i < Graph->Nv; i++)
for (j = 0; j < Graph->Nv; j++)
{
D[i][j] = Graph->G[i][j];
}
for (k = 0; k < Graph->Nv; k++)
for (i = 0; i < Graph->Nv; i++)
for (j = 0; j < Graph->Nv; j++)
if (D[i][k] + D[k][j] < D[i][j])
{
D[i][j] = D[i][k] + D[k][j];
if (i == j && D[i][j] < 0) /* 若发现负值圈*/
return; /* 不能正确解决,返回错误标记*/
}
}
/* 查找二维数组D中第i行的最大值 */
WeightType FindMaxDist( WeightType D[][MaxVertexNum], Vertex i, int N )
{
WeightType MaxDist;
Vertex j;
MaxDist = 0;
for (j = 0; j < N; j++) /* 找出i到其他动物j的最长距离*/
if (i != j && D[i][j] > MaxDist)
MaxDist = D[i][j];
return MaxDist;
}
/* 找到拥有最短路径的动物编号及其路径长度 */
void FindAnimal( MGraph Graph )
{
WeightType D[MaxVertexNum][MaxVertexNum], MaxDist, MinDist;
Vertex Animal, i;
Floyd(Graph, D);
MinDist = INFINITY;
for (i = 0; i < Graph->Nv; i++)
{
MaxDist = FindMaxDist(D, i, Graph->Nv);
if (MaxDist == INFINITY) /* 说明有从i无法变出的动物*/
{
cout << 0 << endl;
return;
}
if (MinDist > MaxDist) /* 找到最长距离更小的动物*/
{
MinDist = MaxDist; /*更新距离*/
Animal = i + 1; /*记录编号*/
}
}
cout << Animal << " " << MinDist << endl;
}
运行结果