58同城前端笔试

1.GET 和 POST安全性比较与讨论

两者最基本区别

1. GET请求通过URL（请求行）提交数据，在URL中可以看到所传参数。POST通过“请求体”传递数据，参数不会在url中显示
2. GET请求提交的数据有长度限制，POST请求没有限制。
3. GET请求返回的内容可以被浏览器缓存起来。而每次提交的POST，浏览器在你按 下F5的时候会跳出确认框，浏览器不会缓存POST请求返回的内容。
4. GET对数据进行查询，POST主要对数据进行增删改！简单说，GET是只读，POST是写。

不同观点

1. 我认为post,更安全一些，因为get传输方式将在URL中显示参数，更容易引发一些“不怀好意”人的兴趣，例如上边出现了username和userpwd等特殊字符时，更容易给他们一些兴趣。虽然可以编码，当是也是可以解码的。而post则对方看不见，即使一些高手截获这些信息，也需要它筛选还有解码，相对来说比get方法更加安全。当然是没有绝对的安全的。
2. HTTP协议中提到GET是安全的方法（safe method），其意思是说GET方法不会改变服务器端数据，所以不会产生副作用。如果是该用POST的地方用了GET，又说GET不安全，那GET也太冤枉了。也就是说，只要我们正确选择使用GET和POST，那么GET是安全的。
3. 只要我们正确使用二者，因为GET方法中不对数据进行修改，不传送一些保密的信息，而这些需要由POST来传输，所以说GET不存在安全问题，而需要注意的是POST传输的安全问题。
4. 正确使用二者，怎么算GET和POST两者正确的选择来使用了。这些规矩或者规范，是怎么制定的呢？为什么说get不能传送加密信息和修改数据呢？原因还是说它没有POST安全，所以HTTP协议规定了它用来传输不重要的读操作，所以才不会因为它而产生安全问题。因为它传送的数据不值得别人去盗取，没有价值。

二.最小化重绘和回流

重绘：将渲染树的每个节点都转换为屏幕上的实际像素

回流：计算节点的位置和几何信息，那么当页面布局和几何信息发生变化的时候，就需要回流。

比如以下情况：

• 添加或删除可见的DOM元素
• 元素的位置发生变化
• 元素的尺寸发生变化（包括外边距、内边框、边框大小、高度和宽度等）
• 内容发生变化，比如文本变化或图片被另一个不同尺寸的图片所替代。
• 页面一开始渲染的时候（这肯定避免不了）
• 浏览器的窗口尺寸变化（因为回流是根据视口的大小来计算元素的位置和大小的）

回流一定会触发重绘，而重绘不一定会回流

最小化重绘和重排

1.合并多次对DOM和样式的修改，然后一次处理掉

2.css3硬件加速（GPU加速）

3.批量修改DOM

当我们需要对DOM对一系列修改的时候，可以通过以下步骤减少回流重绘次数：

1. 使元素脱离文档流

2. 对其进行多次修改

3. 将元素带回到文档中。

该过程的第一步和第三步可能会引起回流，但是经过第一步之后，对DOM的所有修改都不会引起回流，因为它已经不在渲染树了。

有三种方式可以让DOM脱离文档流：

• 隐藏元素，应用修改，重新显示

• 使用文档片段(document fragment)在当前DOM之外构建一个子树，再把它拷贝回文档。

• 将原始元素拷贝到一个脱离文档的节点中，修改节点后，再替换原始的元素。 具体实例可参考https://blog.csdn.net/vM199zkg3Y7150u5/article/details/85042996

三.Vuex--状态管理模式(store/state/Getter/Action/Mutation/Module)

Vuex的核心

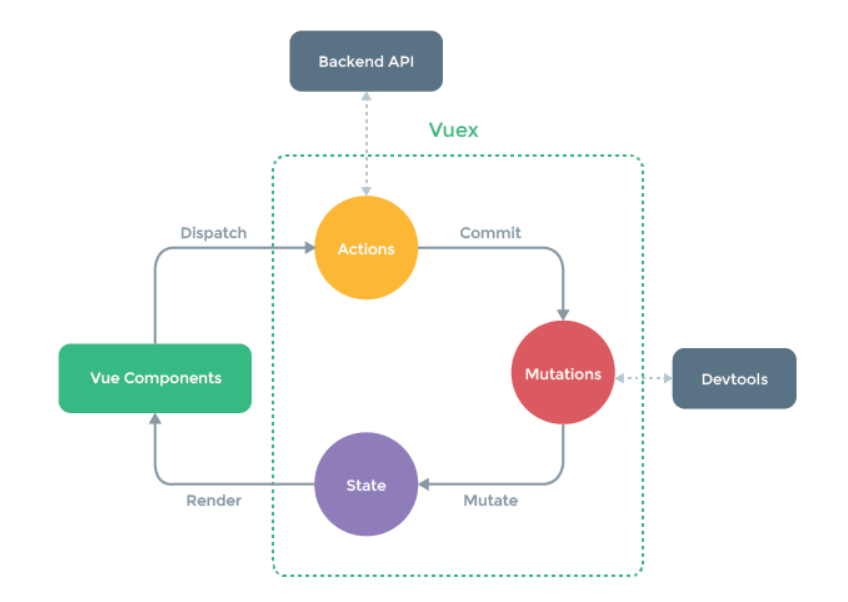
state： Vue 组件中展示状态

Getter：Vuex 允许我们在 store 中定义“getter”（可以认为是 store 的计算属性）。就像计算属性一样，getter 的返回值会根据它的依赖被缓存起来，且只有当它的依赖值发生了改变才会被重新计算。

Action：在组件中使用 this.$store.dispatch(‘xxx’) 分发 action

Mutation：更改 Vuex 的 store 中的状态的唯一方法是提交 mutation。Vuex 中的 mutation 非常类似于事件：每个 mutation 都有一个字符串的 事件类型 (type) 和 一个 回调函数 (handler)。

Module：由于使用单一状态树，应用的所有状态会集中到一个比较大的对象。当应用变得非常复杂时，store 对象就有可能变得相当臃肿。为了解决以上问题，Vuex 允许我们将 store 分割成模块（module）。每个模块拥有自己的 state、mutation、action、getter、甚至是嵌套子模块——从上至下进行同样方式的分割为了解决以上问题，Vuex 允许我们将 store 分割成模块（module）。每个模块拥有自己的 state、mutation、action、getter、甚至是嵌套子模块——从上至下进行同样方式的分割

代码演示https://blog.csdn.net/u011374582/article/details/82799586

四.给出[5<6<3,3<2<4]运行结果

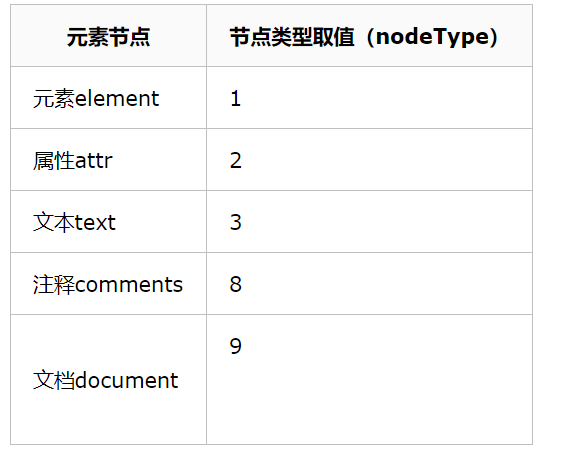
五.nodeType值相对应的文本节点

nodeType是用来获得当前节点对象的类型。

nodeType 属性可返回节点的类型。以下是一些重要的nodeType的取值。

六 编程题.

1.输入一个字符串,输出该字符串中出现次数最多的字符以及出现的次数.

#include<stdio.h>
int main()
{ 
  int k=0,sum[100],d=0;
  char str[100];
  printf("请输入字符串：");
  scanf("%s",str);  
 for(int i=0;str[i]!='';i++)/*####字符串的每一个字符与整个字符串比较#####*/
     {
       for(int j=0;str[j]!='';j++) 
          {
           if(str[j]==str[i])//如果找到相同的字符，K自加1 
             k++;
          }
         sum[i]=k;//把K的值存入SUM数组 
         k=0;//把K清零，便于下次循环的计数 
     } 
  for(int i=0;str[i]!='';i++)//查找SUM数组中的最大值 
  {
     if(sum[0]<sum[i])
      {
       sum[0]=sum[i];
        d=i;//把最大值的位置复制给d 
      } 
  }
   printf("出现次数最多的字符是%c,出现的次数为 %d次
",str[d],sum[d]);//输出出现次数最多的字符以及出现的次数.
  return 0;
}

 2.判断一个字符串中括号是否匹配

从键盘读入一个字符串，其中只含有() {} [ ] ，判断该字符串中的每种括号是否成对出现。

提示：可借助栈来实现，括号必须配对出现，如()[ ]{}，这是匹配的括号，如([{])}，这是不匹配的括号（中间无空格）。

输入描述:
输入一个字符串（中间不包含空格）

输出描述:
匹配输出true，否则输出false

输入样例:
(([{}]))
输出样例:
yes

思路：

1. 括号匹配的四种可能性：

①左右括号配对次序不正确
②右括号多于左括号
③左括号多于右括号
④左右括号匹配正确

2. 算法思想：
1.顺序扫描算数表达式（表现为一个字符串），当遇到三种类型的左括号时候让该括号进栈；
2.当扫描到某一种类型的右括号时，比较当前栈顶元素是否与之匹配，若匹配，退栈继续判断；
3.若当前栈顶元素与当前扫描的括号不匹配，则左右括号配对次序不正确，匹配失败，直接退出；
4.若字符串当前为某种类型的右括号而堆栈已经空，则右括号多于左括号，匹配失败，直接退出；
5.字符串循环扫描结束时，若堆栈非空（即堆栈尚有某种类型的左括号），则说明左括号多于右括号，匹配失败；
6.正常结束则括号匹配正确。

#include <iostream>
#include <cstring>
#include <stack>
 
using namespace std;
 
int main()
{
    stack<char>a;
    int flag=1,i;
    char ch[100];
    cin>>ch;
    for(i=0;i<strlen(ch);i++){
        if(ch[i]=='{'||ch[i]=='('||ch[i]=='[')
            a.push(ch[i]);
        else{
            if(a.empty()==true){
                flag=0;
                break;
            }
            else if((ch[i]=='}'&&a.top()=='{')||(ch[i]==')'&&a.top()=='(')||(ch[i]==']'&&a.top()=='['))
                a.pop();
            else{
                flag = 0;
                break;
            }
        }
    }
    if(flag==0)
        cout<<"false";
    else
        cout<<"true";
}