普通平衡树
题目链接:ybt金牌导航4-3-5 / luogu P3369
题目大意
平衡树模板题,要求维护一些操作。
插入一个数,删除一个数,查询一个数的排名,查询排名一直的数,找前驱后继。
思路
这次我们来讲 Splay 的做法。
Splay 是啥
Splay 树就是一个用翻转来维护平衡的二叉查找树。
而它翻转的条件,其实就是你的查询有关哪个点,它就把那个点旋转到根。
而它的特殊的旋转方式又能使得树的深度变小,所以就维护了平衡。
主要操作:rotate(x) 与 Splay(x,y)
那首先我们来讲旋转:
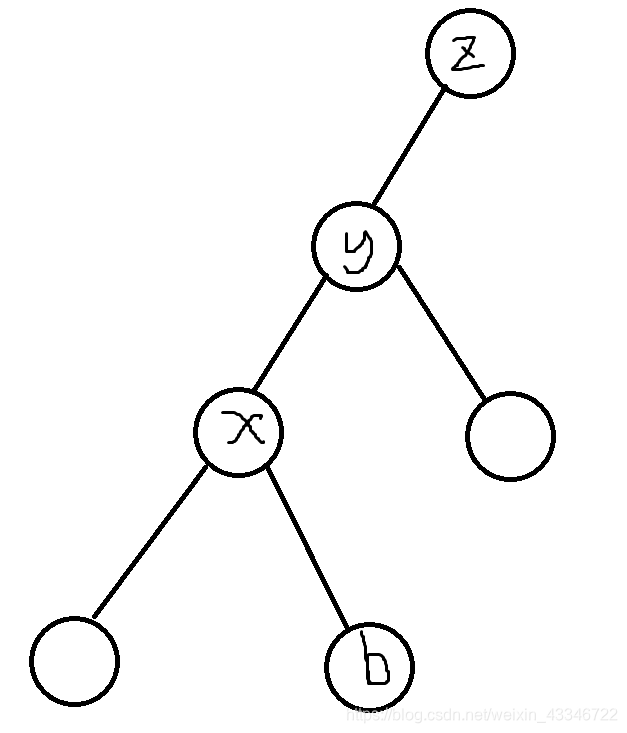
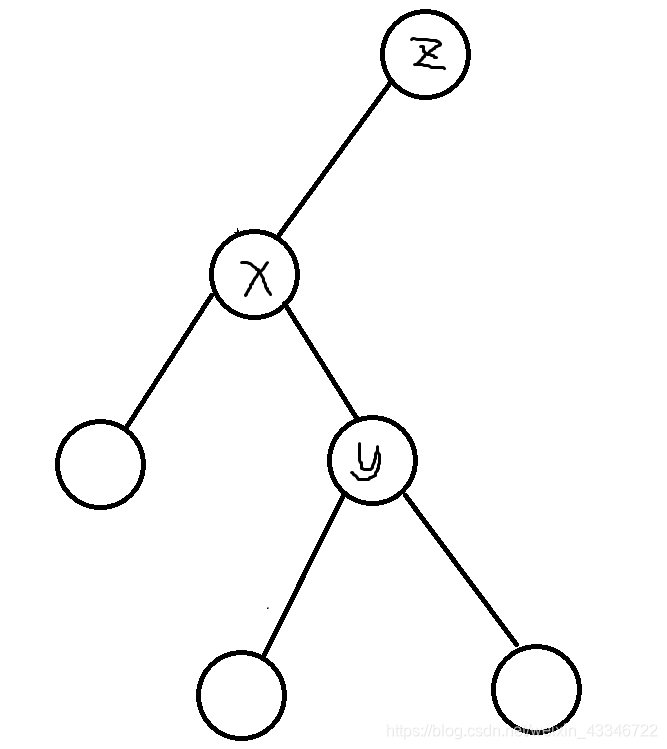
那翻转就是用这两种图的方式,这里如果左图 (x) 右旋,就得到了右图,右图 (y) 左旋,就得到了左图。
而我标出来的点都是有变化的,你只要看着图把它们要改变的值((fa,ls,rs))都按着图改一下,然后就翻转好了。
但一般(这道题也是)的题目还要维护一些东西,比如这个点的子树的大小啊,之类的,那我们翻转之后容易看出要 (up) 重新维护值的就是 (x,y) 两个点。但 (up) 的顺序也要注意,如果是旋 (x),那要先 (up(y)) 在 (up(x))。(按翻转后深度从下到上)
我们为了方便,可以将左旋右旋合到一起,具体可以看看我的 (rotate(x)) 操作。
那接着我们要把一个点 (x) 拎到树根,又要怎么做呢?或者把一个点拎到它某个祖先下面。
那拎到树根其实就相当于拎到 (0) 的下面。
那要怎么搞呢?不难想到,我们知道一直做 (rotate(x)) 知道它是你要的点的儿子就可以。
这样可以是可以,但你会发现树的深度不会减小。
这时候,玄学的做法就出现了,我们分成三种情况:
如果你只用旋一次就够了,就旋一次。
如果要旋转两次以上,而且它和它父亲都是左儿子或都是右儿子,那就先旋父亲再旋它。
如果要旋转两次以上,而且它和它父亲一个左儿子一个右儿子,那就选两次自己。
你画一下图,模拟一下过程,就会发现它真的会缩小深度。
那最后如果你要旋到 (0) 下面,就说明你变成了根节点,那就把根节点的位置给成你的就好了。
具体可以看看我的 (Splay(x,y))。
其它操作
find_up(x)
在平衡树中找 (x) 这个数,并把它拿到根节点的位置。
由于二叉查找数的性质,我们只要从根节点开始,跟当前点比较大小。
一样就是这个位置,小了就是左边,大了就是右边。
找到之后为了方便而且为了维护平衡,我们直接旋转它到根节点。
merge(x,y)
把 (x,y) 点对应的子树合并。
这里有个前提条件,就是 (x) 树中的所有数都一定要小于 (y) 数中的所有数。
那有了这个条件,我们直接 (x) 树一直跳右儿子找到 (x) 树里面最大的,然后拎到根节点,然后右儿子连 (y) 树,维护一下 (fa,ls,rs) 之类的就好了。
val_ask_rnk(x)
找 (x) 这个数的排名,那容易根据二叉查找数的性质想出,我们只要找到它把它拎到根。
然后它左儿子代表的子树大小加一就是它的排名了。
rnk_ask_val(x)
找排名第 (x) 的数。
那这个其实更憨,你就直接从根节点开始找,如果当前你排名小于它左儿子子树大小,那肯定是在那里面。那如果它大于它左儿子子树大小,但小于左儿子子树大小加上你这个点里面包含数的个数(这么说是因为如果数字有重复我们一般会搞一个数组记录这个点里面有多少个这个数),那就是这个数。
否则就在右边,我们把排名减去左子树大小和你这个点里面包含数的个数,然后就去求右子树就可以了。
delete_(x)
把 (x) 数删除。
那容易结合前面的操作,把它放到找到旋到最上面,然后减去点里面这个数的个数。
如果被减到 (0),就说明这个点都要被删掉,那我们就用类似左偏树的做法,把它两个儿子合并即可。
(最好把这个点的信息都清掉,两个儿子的父亲一定要先清成 (0))
spilt(x)【此题未用到】
以 (x) 为界,把大于它和小于它的数分离出来。
那容易想到类似合并的操作,你把它找到旋上了,它的左右两个子树就是小于它和大于它的数了。
get_pre(x)
求 (x) 的前驱,即最大的小于它的数。
那我们容易根据二叉查找数的性质想到这么一个做法。
我们把 (x) 放进平衡树中,找到旋到根,然后从它的左儿子开始一直往右儿子的方向走,最后走到的就是我们要的。
然后搞完之后你还要把 (x) 从平衡树里面删掉,因为你只是询问没有插入,前面为了求你要插入,那你求完就要删掉。
get_nxt(x)
求 (x) 的后继,即最小的大于它的数。
这其实跟上面一样,只是从右儿子开始一直往左儿子的方向走。
关于本题
由于它数会重复,所以你就要搞一个变量记录它一个数有多少次。
然后其他就是平衡树正常操作,搞就完事了。
代码
#include<cstdio>
using namespace std;
int n, op, x, root, tot;
int ls[100001], rs[100001], val[100001], fa[100001], sz[100001];
int sum[100001];
void up(int now) {
sz[now] = sz[ls[now]] + sz[rs[now]] + sum[now];
}
void rotate(int x) {//这些对值的修改是有顺序的,不过你只要先改 fa 再改 ls,rs 应该就不会有问题
int y = fa[x];
int z = fa[y];
int b = (ls[y] == x) ? rs[x] : ls[x];
fa[x] = z;
fa[y] = x;
if (b) fa[b] = y;
if (z) ((ls[z] == y) ? ls[z] : rs[z]) = x;
if (ls[y] == x) ls[y] = b, rs[x] = y;
else rs[y] = b, ls[x] = y;
up(y);
up(x);
}
bool whs(int x) {//判断是左儿子还是右儿子
return ls[fa[x]] == x;
}
void Splay(int x, int father) {//按着玄学的旋转方式搞
while (fa[x] != father) {
if (fa[fa[x]] != father) {
if (whs(x) == whs(fa[x])) rotate(fa[x]);
else rotate(x);
}
rotate(x);
}
if (!father) root = x;//旋到了根节点
}
void insert(int num) {
int x = root, y = 0, way = 0;
while (x) {
y = x;
sz[x]++;
if (num < val[x]) x = ls[x], way = 0;
else if (num > val[x]) x = rs[x], way = 1;
else {//重复出现的就不要新开点了,直接记录个数
sum[x]++;
sz[x]++;
Splay(x, 0);
return ;
}
}
x = ++tot;
fa[x] = y;
if (y) (way ? rs[y] : ls[y]) = x;
sz[x] = 1;
sum[x] = 1;
val[x] = num;
Splay(x, 0);
}
void find_up(int num) {
int now = root;
while (now) {//按着二叉查找树的性质找
if (val[now] == num) break;
if (val[now] < num) now = rs[now];
else now = ls[now];
}
if (now) Splay(now, 0);
}
int merge(int l, int r) {
fa[l] = 0;
fa[r] = 0;
if (!l) return r;
if (!r) return l;
int x = l, y = 0;
while (x) {
y = x;
x = rs[x];
}
Splay(y, 0);
fa[r] = y;
rs[y] = r;
up(y);
return y;
}
void delete_top() {
int tmp = root;
sz[tmp] = 0;
root = merge(ls[root], rs[root]);
ls[tmp] = rs[tmp] = 0;
}
int val_ask_rnk(int x) {
find_up(x);
return sz[ls[root]] + 1;
}
int rnk_ask_val(int rnk) {//注意你询问排名的时候中间大小不再是一,而是这个数出现的次数
int now = root;
while (now) {
if (rnk > sz[ls[now]] && rnk <= sz[ls[now]] + sum[now]) return val[now];
if (rnk <= sz[ls[now]]) now = ls[now];
else rnk -= sz[ls[now]] + sum[now], now = rs[now];
}
}
int get_pre(int num) {
find_up(num);
int x = ls[root], y = 0;
while (x) {
y = x;
x = rs[x];
}
return val[y];
}
int get_nxt(int num) {
find_up(num);
int x = rs[root], y = 0;
while (x) {
y = x;
x = ls[x];
}
return val[y];
}
void delete_(int x) {
find_up(x);
sum[root]--;//减的时候先减个数,如果全部减完了再删点
if (!sum[root]) delete_top();
}
int main() {
// freopen("write.txt", "w", stdout);
scanf("%d", &n);
while (n--) {
scanf("%d %d", &op, &x);
if (op == 1) {
insert(x);
continue;
}
if (op == 2) {
delete_(x);
continue;
}
if (op == 3) {
printf("%d
", val_ask_rnk(x));
continue;
}
if (op == 4) {
printf("%d
", rnk_ask_val(x));
continue;
}
if (op == 5) {
insert(x);
printf("%d
", get_pre(x));
delete_(x);
continue;
}
if (op == 6) {
insert(x);
printf("%d
", get_nxt(x));
delete_(x);
continue;
}
}
return 0;
}