1 树
1.1 定义
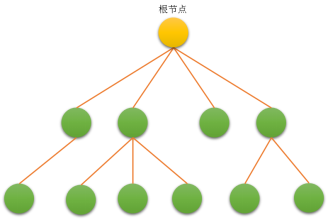
由一个或多个(n ≥ 0)结点组成的有限集合 T,有且仅有一个结点称为根(root),当 n > 1 时,其余的结点分为 m (m ≥ 0)个互不相交的有限集合T1,T2,…,Tm。每个集合本身又是棵树,被称作这个根的子树 。
1.2 结构特点
-
非线性结构,有一个直接前驱,但可能有多个直接后继(1:n)
-
树的定义具有递归性,树中还有树。
-
树可以为空,即节点个数为0。
1.3 术语
-
根:即根结点(没有前驱)
-
叶子:即终端结点(没有后继)
-
森林:指m棵不相交的树的集合(例如删除A后的子树个数)
-
有序树:结点各子树从左至右有序,不能互换(左为第一)
-
无序树:结点各子树可互换位置。
-
双亲:即上层的那个结点(直接前驱) parent
-
孩子:即下层结点的子树 (直接后继) child
-
兄弟:同一双亲下的同层结点(孩子之间互称兄弟)sibling
-
堂兄弟:即双亲位于同一层的结点(但并非同一双亲)cousin
-
祖先:即从根到该结点所经分支的所有结点
-
子孙:即该结点下层子树中的任一结点
-
结点:即树的数据元素
-
结点的度:结点挂接的子树数(有几个直接后继就是几度)
-
结点的层次:从根到该结点的层数(根结点算第一层)
-
终端结点:即度为 0 的结点,即叶子
-
分支结点:除树根以外的结点(也称为内部结点)
-
树的度:所有结点度中的最大值(Max{各结点的度})
-
树的深度(或高度):指所有结点中最大的层数(Max{各结点的层次})

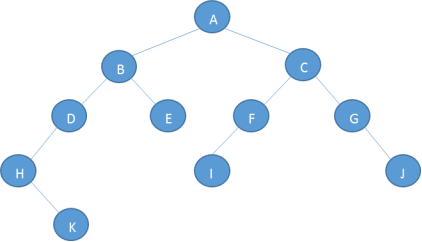
上图中的结点数= 13,树的度= 3,树的深度= 4
1.4 树的表示法
1.4.1 广义表表示法
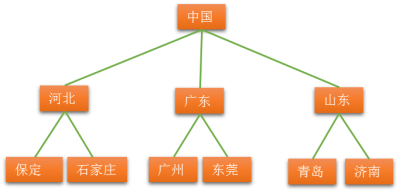
用广义表表示法表示上图:
中国(河北(保定,石家庄),广东(广州,东莞),山东(青岛,济南))
根作为由子树森林组成的表的名字写在表的左边
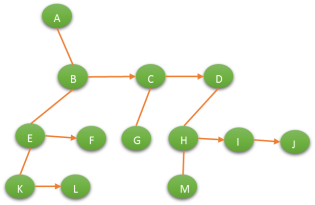
1.4.2 左孩子右兄弟表示法
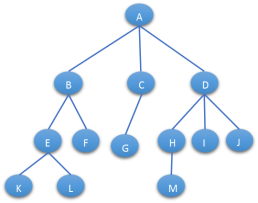
左孩子右兄弟表示法可以将一颗多叉树转化为一颗二叉树:
节点的结构:

节点有两个指针域,其中一个指针指向子节点,另一个指针指向其兄弟节点。
1.5 树的结构
1.5.1 逻辑结构
一对多(1:n),有多个直接后继(如家谱树、目录树等等),但只有一个根结点,且子树之间互不相交。
1.5.2 存储结构
树的存储仍然有两种方式:
- 顺序存储
可规定为:从上至下、从左至右将树的结点依次存入内存。
重大缺陷:复原困难(不能唯一复原就没有实用价值)。
- 链式存储
可用多重链表:一个前趋指针,n个后继指针。
细节问题:树中结点的结构类型样式该如何设计?
即应该设计成“等长”还是“不等长”?
缺点:等长结构太浪费(每个结点的度不一定相同);
不等长结构太复杂(要定义好多种结构类型)。
以上两种存储方式都存在重大缺陷,应该如何解决呢?
计算机实现各种不同进制的运算是通过先研究最简单、最有规律的二进制运算规律,然后设法把各种不同进制的运算转化二进制运算。树的存储也可以通过先研究最简单、最有规律的树,然后设法把一般的树转化为这种简单的树,这种树就是 二叉树。
2 二叉树
2.1 定义
n(n ≥ 0)个结点的有限集合,由 一个根结点 以及 两棵互不相交的、分别称为左子树和右子树的 二叉树 组成 。
2.2 逻辑结构
一对二(1:2)
2.3 基本特征
-
每个结点最多只有两棵子树(不存在度大于2的结点)
-
左子树和右子树次序不能颠倒(有序树)
2.4 基本形态
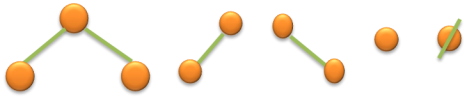
2.5 二叉树的性质
-
性质1: 在二叉树的第 i 层上至多有 ({2^{i-1}}) 个结点(i > 0)
-
性质2: 深度为 k 的二叉树至多有 ({2^{k-1}}) 个结点(k > 0)
-
性质3: 对于任何一棵二叉树,若 2 度的结点数有 n2 个,则叶子数(n0)必定为 n2+1 (即 n0 = n2 + 1)
满二叉树:一棵深度为k 且有 ({2^{k-1}}) 个结点的二叉树。
特点:每层都“充满”了结点
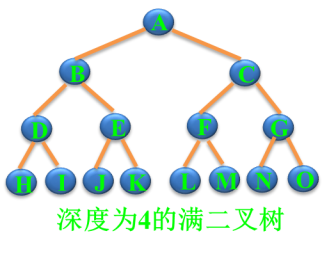
完全二叉树:深度为 k 的,有 n 个结点的二叉树,当且仅当其每一个结点都与深度为 k 的满二叉树中编号从 1 至 n 的结点一一对应。

-
性质4: 具有 n 个结点的完全二叉树的深度必为 ({log_{2}n} +{1})
-
性质5: 对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为 2i,其右孩子编号必为 2i+1。其双亲的编号必为i/2(i=1 时为根,除外)
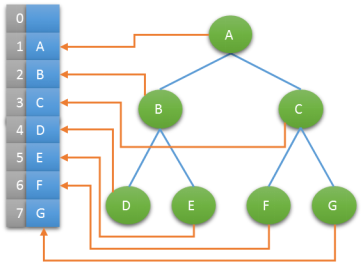
使用此性质可以使用完全二叉树实现树的顺序存储。
2.2 二叉树的表示
2.2.1 二叉链表 表示法
一般从根结点开始存储。相应地,访问树中结点时也只能从根开始。
存储结构:
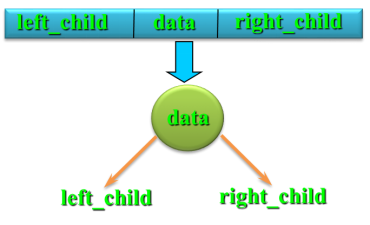
结点数据类型定义:
typedef struct BiTNode
{
int data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
2.2.2 三叉链表 表示法
存储结构:

每个节点有三个指针域,其中两个分别指向子节点(左孩子,右孩子),还有一共指针指向该节点的父节点。
结点数据类型定义:
//三叉链表
typedef struct TriTNode
{
int data;
//左右孩子指针
struct TriTNode *lchild, *rchild;
struct TriTNode *parent;
}TriTNode, *TriTree;
2.2.3 双亲 表示法
存储结构:

每个节点都由一个数据结构组成,每个节点顺序排放在数组中。
结点数据类型定义:
//双亲链表
#define MAX_TREE_SIZE 100
typedef struct BPTNode
{
int data; // 数据
int parentPosition; //指向双亲的指针,数组下标
char LRTag; //左右孩子标志域
}BPTNode;
typedef struct BPTree
{
//因为节点之间是分散的,需要把节点存储到数组中
BPTNode nodes[100];
int num_node; //节点数目
//根结点的位置,注意此域存储的是父亲节点在数组的下标
int root;
}BPTree;
2.3 二叉树的遍历
定义:指按某条搜索路线 遍访每个结点且不重复。
遍历方法:
牢记一种约定,对每个结点的查看都是“先左后右” 。
限定先左后右,树的遍历有三种实现方案:
DLR LDR LRD
先 (根)序遍历 中 (根)序遍历 后(根)序遍历
-
DLR:先序遍历,即先根再左再右
-
LDR:中序遍历,即先左再根再右
-
LRD: 后序遍历,即先左再右再根
注:“先、中、后”的意思是指访问的结点 D 是先于子树出现还是后于子树出现。
2.3.1 先序遍历
PreOrder(NODE *root )
{
if (root) //非空二叉树
{
printf(“%d”,root->data); //访问D
PreOrder(root->lchild); //递归遍历左子树
PreOrder(root->rchild); //递归遍历右子树
}
}
2.3.2 中序遍历
InOrder(NODE *root)
{
if(root !=NULL)
{
InOrder(root->lchild);
printf(“%d”,root->data);
InOrder(root->rchild);
}
}
2.3.3 后序遍历
PostOrder(NODE *root)
{
if(root !=NULL)
{
PostOrder(root->lchild);
PostOrder(root->rchild);
printf(“%d”,root->data);
}
}
2.3.4 三种遍历的本质
从前面的三种遍历算法可以知道:如果将printf语句抹去,除去printf的遍历算法:
XXX (NODE *root)
{
if(root)
{
XXX(root->lchild);
XXX(root->rchild);
}
}
从递归的角度看,这三种算法是完全相同的,或者说这三种遍历算法的访问路径是相同的,只是访问结点的时机不同。
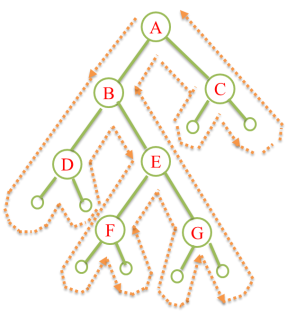
从虚线的出发点到终点的路径上,每个结点经过 3 次。
-
第 1 次经过时访问=先序遍历
-
第 2 次经过时访问=中序遍历
-
第 3 次经过时访问=后序遍历
2.4 二叉树的创建
2.4.1 先序和中序 创建树
算法
-
通过先序遍历找到根结点A,再通过A在中序遍历的位置找出左子树,右子树
-
在A的左子树中,找左子树的根结点(在先序中找),转步骤1
-
在A的右子树中,找右子树的根结点(在先序中找),转步骤1
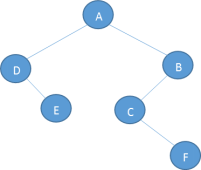
练习1:
先序遍历结果:A D E B C F
中序遍历结果:D E A C F B
解:
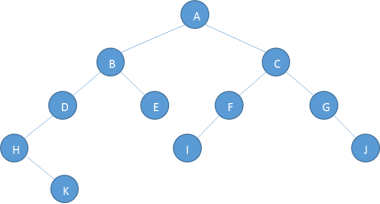
练习2:
先序遍历结果:A B D H K E C F I G J
中序遍历结果:H K D B E A I F C G J
解:
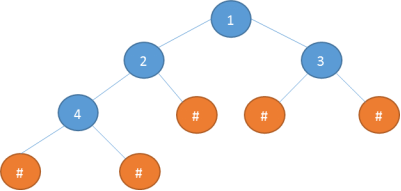
2.4.2 # 号法 创建树
什么是 # 号法创建树:# 创建树,让树的每一个节点都变成度数为 2 的树
例子1: 124###3##
解:
例子2:先序遍历:A B D H # K # # # E # # C F I # # # G # J # #,请画出树的形状
解:
# 号法编程实践:
利用前序遍历来建树:
Bintree createBTpre( )
{ Bintree T; char ch;
scanf(“%c”,&ch);
if(ch==’#’) T=NULL;
else
{ T=( Bintree )malloc(sizeof(BinTNode));
T->data=ch;
T->lchild=createBTpre();
T->rchild=createBTpre();
}
return T;
}
使用后序遍历的方式销毁一棵树, 先释放叶子节点,在释放根节点:
void BiTree_Free(BiTNode* T)
{
BiTNode *tmp = NULL;
if (T!= NULL)
{
if (T->rchild != NULL) BiTree_Free(T->rchild);
if (T->lchild != NULL) BiTree_Free(T->lchild);
if (T != NULL)
{
free(T);
T = NULL;
}
}
}
3 霍夫曼树
3.1 概念
组建一个网络,耗费最小 WPL(树的带权路径长度)最小,称为 霍夫曼树。
从树中一个节点到另一个节点之间的分支构成两个节点之间的路径,路径上的分支数目称作 路径长度。
例子:
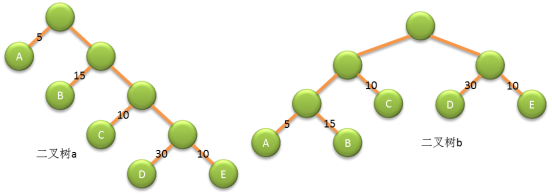
如下图的二叉树 a 中,根节点到节点 D 的路径长度为 4,二叉树 b 中根节点到节点 D 的路径长度为 2。树的路径长度就是从树根到每一节点的路径长度之和。二叉树 a 的树路径长度就为 1+1+2+2+3+3+4+4=20。二叉树 b 的树路径长度为 1+2+3+3+2+1+2+2=16。
3.2 霍夫曼树的构造
对于文本”BADCADFEED”的传输而言,因为重复出现的只有“ABCDEF”这6个字符,因此可以用下面的方式编码:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 000 | 001 | 010 | 011 | 100 | 101 |
B A D C A D F E E D 001 000 011 010 000 011 101 100 100 011
接收方可以根据每 3 个 bit 进行一次字符解码的方式还原文本信息。这样的编码方式需要 30 个 bit 位才能表示 10 个字符那么当传输一篇 500 个字符的情报时,需要 15000 个 bit 位,在战争年代,这种编码方式对于情报的发送和接受是很低效且容易出错的。如何提高收发效率?
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 01 | 1001 | 101 | 00 | 11 | 1000 |
B A D C A D F E E D 1001 01 00 101 01 00 1000 11 11 00
准则:任一字符的编码都不是另一个字符编码的前缀!
也就是说:每一个字符的编码路径,都不包含另外一个字符的路径。
3.2.1 构建规则
-
给定 n 个数值{ v1, v2, …, vn}。
-
根据这 n 个数值构造二叉树集合 F = { T1, T2, …, Tn},Ti 的数据域为 vi,左右子树为空。
-
在 F 中选取两棵根结点的值最小的树作为左右子树构造一棵新的二叉树,这棵二叉树的根结点中的值为左右子树根结点中的值之和
-
在 F 中删除这两棵子树,并将构造的新二叉树根节点加入 F 中
-
重复 3 和4,直到 F 中只剩下一个树为止。
这棵树即 霍夫曼树
3.2.2 特点
-
所用的字符都作为叶子节点出现。
-
根到每个字符的路径都不重复,也不存在重叠的现象。
3.2.3 特点
-
霍夫曼树是一种特殊的二叉树。
-
霍夫曼树应用于信息编码和数据压缩领域。
-
霍夫曼树是现代压缩算法的基础。