列表排序:
将无序的列表变为有序列表
应用场景:
各种榜单排序、各种表格排序、给二分排序用、给其他算法用等等
算法关键点:有序区、无序区
排序low B 三人组:
冒泡排序: # 面试常考
思路:首先,列表中两个相邻的数,如果前边的比后面的大,那么交换着两个数。。。
代码:
1 # -*- coding:utf-8 -*- 2 # @File : bubble_sort.py 3 # @Author : Clint 4 import random 5 6 7 def bubble_sort(data_list): # 冒泡排序 O(n^2) 8 for i in range(len(data_list)-1): 9 for j in range(len(data_list)-i-1): 10 if data_list[j] < data_list[j+1]: 11 data_list[j], data_list[j+1] = data_list[j+1], data_list[j] 12 13 14 data = list(range(100)) 15 random.shuffle(data) # 洗牌函数,将有序的列表打乱 16 bubble_sort(data) 17 print(data)
优化后的冒泡排序
1 # -*- coding:utf-8 -*- 2 # @Author : Clint 3 4 5 def bubble_sort(data_list): # 优化后的冒泡排序 最好情况下的时间复杂时间是O(n) 6 for i in range(len(data_list)-1): 7 exchange = False 8 for j in range(len(data_list)-i-1): 9 if data_list[j] < data_list[j+1]: 10 data_list[j], data_list[j+1] = data_list[j+1], data_list[j] 11 exchange = True 12 if not exchange: 13 break
选择排序:
思路:一趟遍历最小的数,放到第一个位置;再一趟遍历剩余列表中最小的数,继续放置;... 排序完成。
问题:怎么选出最小的数?
代码:
1 # -*- coding:utf-8 -*- 2 # @Author : Clint 3 # @File : select_sort.py 4 5 6 def select_sort(data_list): # 选择排序 O(n^2) 7 for i in range(len(data_list)-1): 8 min_loc = i 9 for j in range(i+1, len(data_list)): 10 if data_list[j] < data_list[min_loc]: 11 min_loc = j 12 data_list[i], data_list[min_loc] = data_list[min_loc], data_list[i] 13 14 15 data = [3, 5, 7, 4, 2, 6, 33, 0, 54] 16 select_sort(data) 17 print(data)
插入排序:
思路:列表被分为有序区和无序区两个部分,最初有序区只有一个元素;每次从无序区选择一个元素,插入到有序区的位置,直到无序区变空
代码:
# -*- coding:utf-8 -*- # @Author : Clint def insert_sort(data_list): # 插入排序 O(n^2) for i in range(1, len(data_list)): temp = data_list[i] j = i-1 while j >= 0 and data_list[j] > temp: data_list[j+1],data_list[j] = data_list[j], temp
j -= 1
data = [7,5,8,6,3,1,2,9,0]
insert_sort(data)
print(data)
PS: 插入排序有个优化空间:应用二分查找来寻找插入点
快速排序:
思路:取一个元素p(第一个元素),使元素p归位;列表被p分成两部分,左边都比p小,右边都比p大;递归完成排序
算法关键点:1.整理;2.递归
代码:
# -*- coding:utf-8 -*- # @Author : Clint data = [7, 5, 8, 6, 3, 1, 2, 9, 0] def quick_sort(data_list, left, right): # 快速排序 O(nlogn) if left < right: mid = partition(data_list, left, right) quick_sort(data_list, left, mid-1) quick_sort(data_list, mid+1, right) def partition(data_list, left, right): temp = data_list[left] while left < right: while left < right and data_list[right] >= temp: right -= 1 data_list[left] = data_list[right] while left < right and data_list[left] <= temp: left += 1 data_list[right] = data_list[left] data_list[left] = temp return left quick_sort(data, 0, len(data)-1) print(data)
*排序NB二人组:
堆排序:
应准备的知识点:
树:
1.树是一种数据库结构,如:目录结构
2.树是一种可以递归定义的数据结构
3.树是由n个节点组成的集合:
如果n=0,那这是一颗空树;
如果n>0,那存在1个节点作为树的 根节点,其他节点可以分为m个集合,每个集合本身又是一棵树。
相关概念:根节点、叶子节点;树的深度(高度);树的度;孩子节点、父节点;子树等等;
二叉树:
二叉树的储存方式:链式储存、顺序存储(列表)
堆:
大根堆:一颗完全二叉树,满足任一节点都比其孩子节点大
小根堆:一颗完全二叉树,满足任一节点都比其孩子节点小
思路:
1.建立堆(sift);
2.得到堆顶,为最大元素
3.去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序;
4.堆顶元素为第二大元素;
5.重复步骤3,直到堆变空;
代码:
# -*- coding:utf-8 -*- # @Author : Clint data = [7, 5, 8, 6, 3, 1, 2, 9, 0] # 升序 建大根堆 def sift(data_list, low, high): i = low # 最开始的父节点 j = 2*i+1 # 最开始的左子节点 tmp = data_list[i] while j <= high: # 如果子节点没到子树的最后,那么继续 if data_list[j] < data_list[j+1] and j+1 <= high: j += 1 if tmp < data_list[j]: # 如果父节点比子节点小 data_list[i] = data_list[j] # 那么父子节点互换 i = j # 字节点成为父节点 j = 2*i+1 # 新子节点 else: break data_list[i] = tmp def heap_sort(data_list): n = len(data_list) for i in range(n//2 - 1, -1, -1): sift(data_list, i, n-1) # 堆建好了 for i in range(n-1, -1, -1): # i指向堆的最后 data_list[0], data_list[i] = data_list[i], data_list[0] # 父节点出局,堆的最后叶子节点上位 sift(data_list, 0, i-1) # 调整出新的父节点 heap_sort(data) print(data) # 升序排列,若要降序排列,则建小根堆即
归并排序
思路:
1.将列表越分越小,直至分成一个元素;
2.把一个元素理解成是是有序的;
3.合并:将两个有序列表归并,列表越来越大;
代码:
# -*- coding:utf-8 -*- # @Author : Clint import sys import random sys.setrecursionlimit(1000) def one_merge(data_list, low, mid, high): # 一次归并 i = low j = mid + 1 lda = [] while i <= mid and j <= high: if data_list[i] < data_list[j]: lda.append(data_list[i]) i += 1 else: lda.append(data_list[j]) j += 1 while i <= mid: lda.append(data_list[i]) i += 1 while j <= high: lda.append(data_list[j]) j += 1 data_list[low:high+1] = lda def merge_sort(data_list, low, high): # 合并排序 O(nlogn) if low < high: mid = (low + high)//2 merge_sort(data_list, low, mid) # 递归实现 merge_sort(data_list, mid+1, high) one_merge(data_list, low, mid, high) data = list(range(100)) random.shuffle(data) # 洗牌函数,将有序的列表打乱 print(data) merge_sort(data, 0, len(data)-1) print(data)
快速排序、堆排序、归并排序---来个小结
三种排序的时间复杂度都是O(nlogn),一般情况下 就运行时间:快排 < 归排 < 堆排;
三种排序也各有缺点:快排:极端情况下效率低;归排:需要额外的内存开销;堆排:在快的排序算法中相对较慢。
PS:在练习这些算法时,我们可以写一个计算函数运行时间的装饰器,边写边测试;
代码:
# -*- coding:utf-8 -*- # @Author : Clint # @File : calculate_time.py import time def cal_time(func): def wrapper(*args, **kwargs): start_time = time.time() x = func(*args, **kwargs) end_time = time.time() print(func.__name__+"的Time cost:", end_time-start_time) return x return wrapper
PPS:在有递归的排序算法中我们需要注意两点;
1.python最大递归数为999,我们可以设置如:
import sys sys.setrecursionlimit(10000) # 将递归数设置为10000
2.将有递归的函数进行封装再加装饰器如:
@cal_time def merge_sort1(data_list): _merge_sort(data_list, 0, len(data_list)) # 执行归并排序的函数
希尔排序
实质上是一种分组的插入排序;
思路:
1.首先取一个整数d1 = n / 2,将元素分为d1个组,每组相邻的元素之间距离为d1,在各组内进行直接插入排序;
2.取第二个整数d2 = d1 / 2 ,重复上述分组排序过程,直到 di = 1,既所有元素在同一组内进行直接插入排序;
PS:希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。
代码:
# -*- coding:utf-8 -*- # @Author : Clint def shell_sort(data_list): # 希尔排序 O(n(1+T)) gap = len(data_list) // 2 while gap > 0: for i in range(gap, len(data_list)): temp = data_list[i] j = i-gap while j >= 0 and temp < data_list[j]: data_list[j+gap] = data_list[j] j -= gap data_list[j+gap] =temp gap /= 2
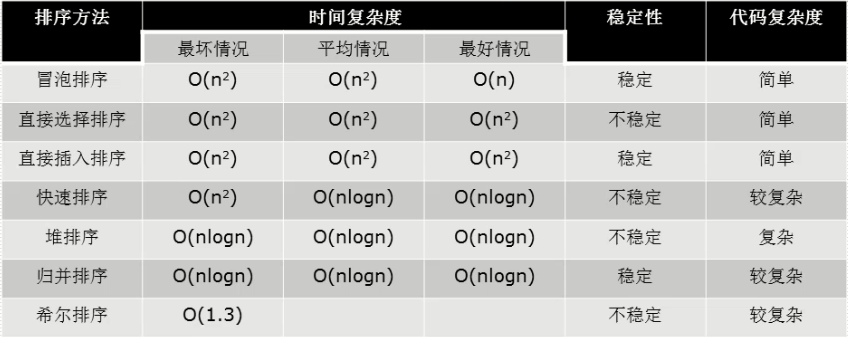
最后借张图来总结一下: