20172303 2018-2019-1《程序设计与数据结构》第8周学习总结
教材学习内容总结
本周的内容又是一次延续上一周学习内容掌握新知识的过程,本周学习了一种特殊形式的树——堆,学习了两种实现堆的方法:用链表实现和用数组实现,同时还学习了使用堆来实现一种特殊队列——优先队列以及基于堆实现的另一种排序方法:堆排序。
一、堆的概述
- 概念:堆是一种具有两种附加属性的特殊二叉树。
- 附加属性一:堆是一颗完全树(复习:完全树:底层叶子都位于树的左边的平衡树称为完全树)
- 附加属性二:对于堆中的每一个结点,该结点都小于或等于(大于或等于)它的左右孩子。
- 类型:
- 最小堆(小顶堆)——堆中每一个结点都小于等于其左右孩子的堆
- 最大堆(大顶堆)——堆中每一个结点都大于等于其左右孩子的堆
- 特点:
- 堆的最小值/最大值存储在根处
- 堆的每一颗子树也是一个堆
二、堆的操作
(一)堆的构造(以构造大顶堆为例)
- 第一步:将元素按照层序遍历的顺序构造一颗二叉树
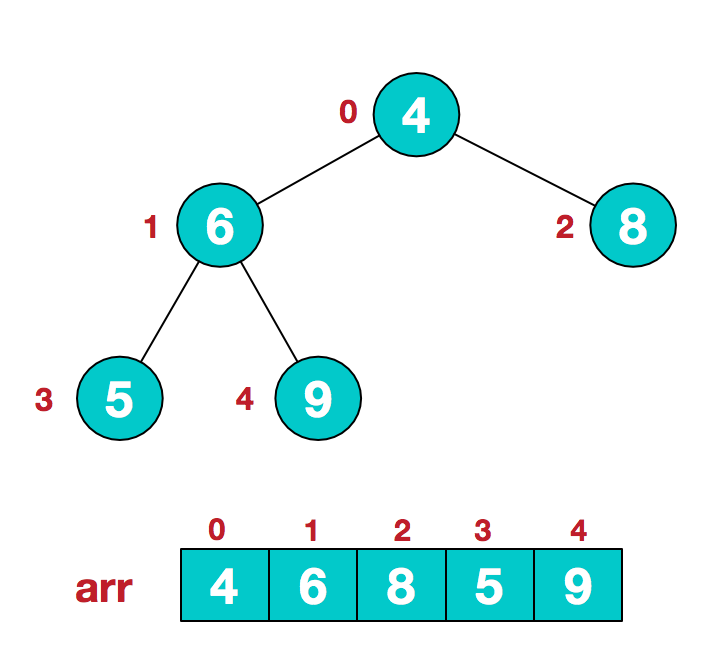
- 第二步:从树中的第一个非叶子结点/非终端结点(寻找方法:树中的第[树中元素个数/2]个元素)开始调整,判断该结点与其孩子的大小,如果不满足堆的附加属性二则进行交换。如在下图中,第一个非叶子结点为
6,它和它的右孩子9与堆的附加属性二冲突,所以将两者进行交换。
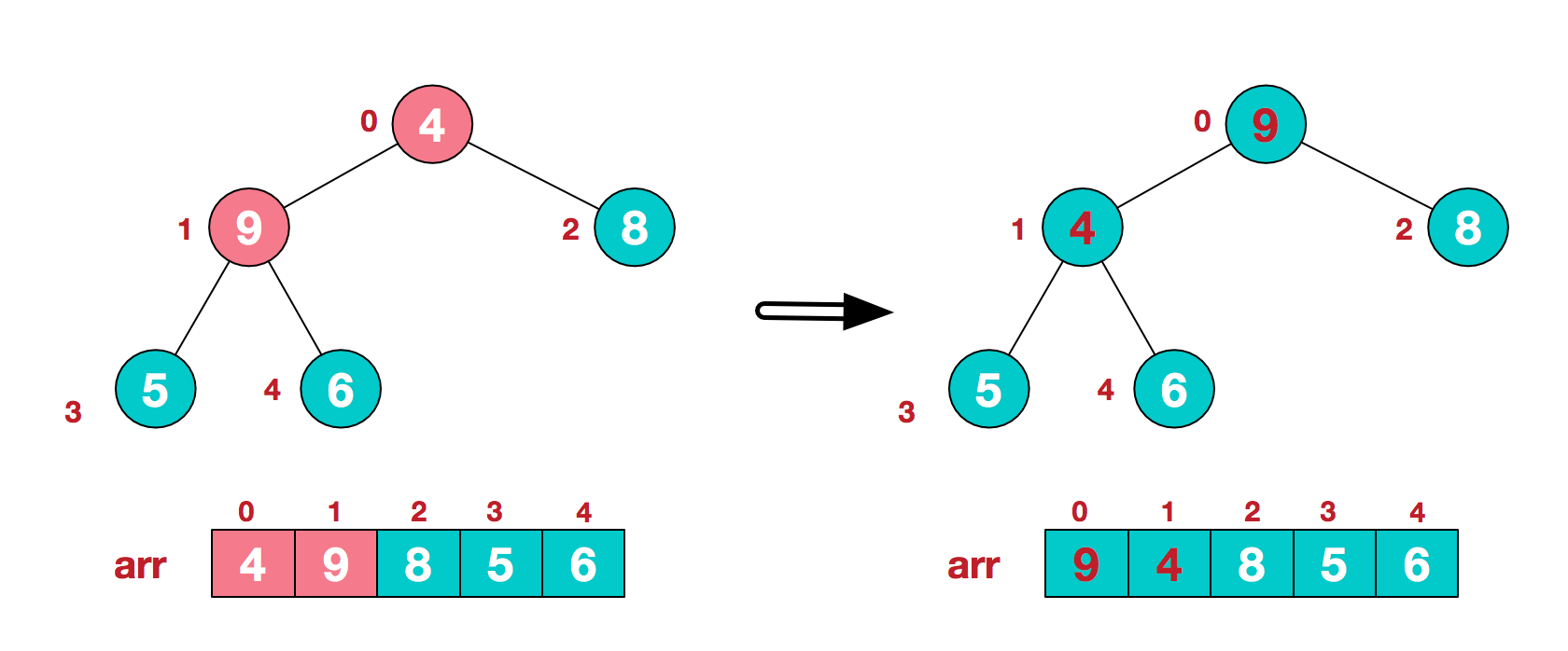
- 第三步:向上继续寻找下一个非叶子结点直至根结点,重复上一步操作,如果在交换之后存在新的不平衡,那么针对与孩子交换之后的非叶子结点,与其新的左右孩子再次进行对比和交换。如在下图中,第二个非叶子结点为
4,它比它的两个孩子都小,所以与其中较大的9进行交换,而在交换之后,4与它新的左孩子5和右孩子6进行对比,仍然与堆的附加属性二冲突,所以再次对4和6进行交换操作。
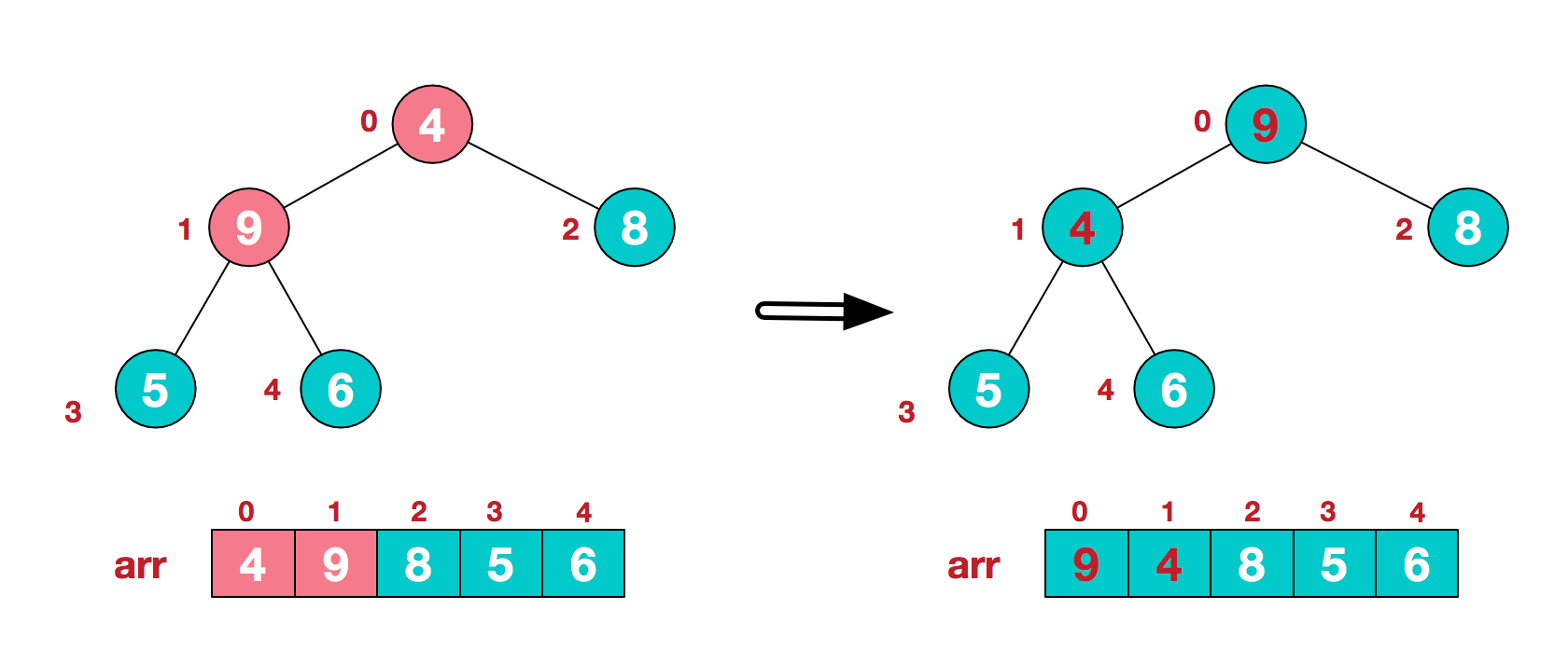
(二)添加操作(以小顶堆中的插入为例)
- 第一步——插入
- 对于插入堆中的元素来说,插入时只会有一个正确的插入位置,而这个插入位置有两种可能,假设堆的层数为h,插入元素的位置要么在第h层的下一个靠左的空位置,要么在第h+1层的第一个位置。
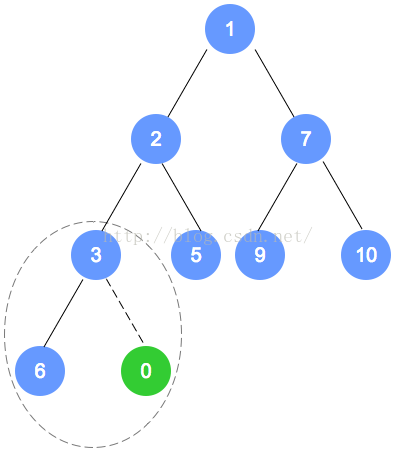
- 对于插入堆中的元素来说,插入时只会有一个正确的插入位置,而这个插入位置有两种可能,假设堆的层数为h,插入元素的位置要么在第h层的下一个靠左的空位置,要么在第h+1层的第一个位置。
- 第二步——调整
- 在插入之后,将插入的元素与其父结点进行对比,如果不满足堆的附加属性二,则将其元素与其父结点进行对比,在必要时进行交换,直至该元素与其父结点满足附加属性二或位于该堆的根处。
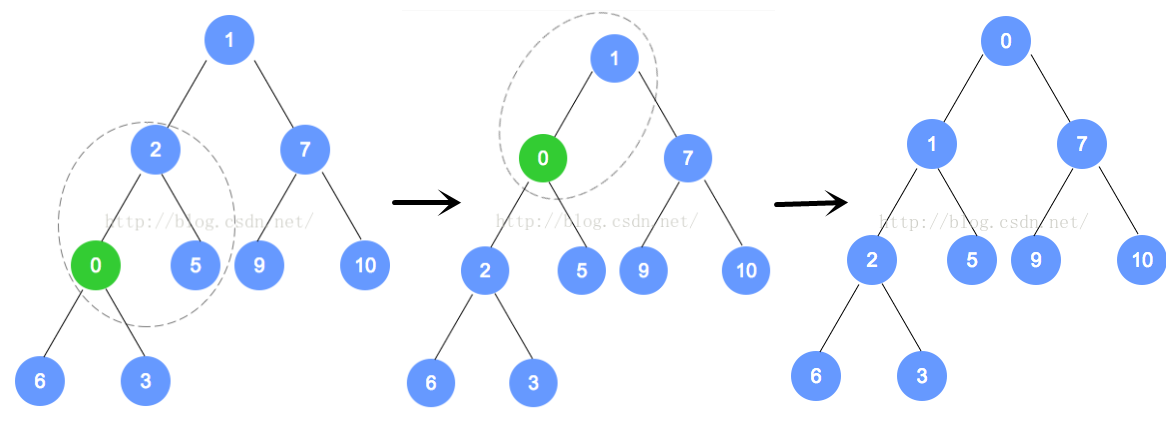
- 在插入之后,将插入的元素与其父结点进行对比,如果不满足堆的附加属性二,则将其元素与其父结点进行对比,在必要时进行交换,直至该元素与其父结点满足附加属性二或位于该堆的根处。
(三)删除操作(以小顶堆中的删除为例)
- 堆中的删除操作是针对堆的根结点来进行的。
- 第一步——删除
- 首先将堆的根结点删除,然后将堆中原来的最后一个元素替换到根结点处。
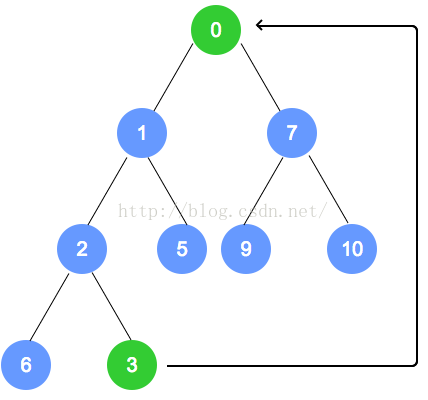
- 首先将堆的根结点删除,然后将堆中原来的最后一个元素替换到根结点处。
- 第二步——调整
- 从根结点处向下,将根结点与其左右孩子进行对比,如果不符合堆的附加属性二,则继续交换,交换之后继续与新的左右孩子进行比较交换,直至该元素与其左右孩子满足附加属性二或位于该堆的叶子处。
三、堆的实现
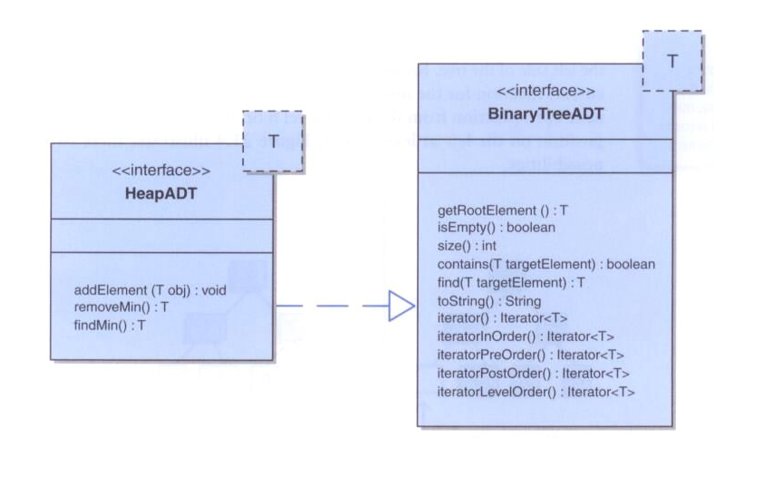
(一)用链表实现堆
- 因为我们要求在插入元素后能够向上遍历该树,所以堆中结点必须存在指向其双亲的指针。除此之外,为了能够追踪堆中的最末一片叶子,还要设置一个
lastNode来存储最末结点。 addElement- 该操作有三个步骤:
- 添加新的元素到末尾,在该步骤中要确定插入结点的双亲,在最坏的情况下,它可能将整个堆遍历,这个过程的时间复杂度为O(logn)。
- 对堆进行重新调整,在调整过程中最多要进行logn次比较,及从下至上遍历每一层(如果堆中有n个元素,则其高度为logn),所以其时间复杂度为O(logn)。
- 将
lastNode指针再次指向最末的结点,该步的时间复杂度为O(1)。
- 所以添加操作的时间复杂度为O(logn)。
- 在这个方法中应用了两个私有方法
getNextParentAdd(用于返回插入结点现在的父结点)和heapifyAdd(从该结点开始,对剩余堆进行重新调整直至根处)。
- 该操作有三个步骤:
removeMin- 该操作有三个步骤:
- 用堆中的最末结点替换根结点,该步的时间复杂度为O(1)。
- 在必要的情况下,对堆进行重新排序。该步操作与添加中的第二步类似,因此其时间复杂度为O(logn)。
- 确定新的最末结点,在最坏的情况下,我们需要遍历整个堆才能找到最末结点,此时它的时间复杂度为O(logn)。
- 所以删除操作的时间复杂度为O(logn)。
- 在这个方法中同样应用了两个私有方法
getNewLastNode(用于返回最末结点的引用)和heapifyRemove(从根结点开始,对下面的堆进行重新调整直至叶子结点)。
- 该操作有三个步骤:
(二)用数组实现堆
- 在用数组建立的堆中,根位于数组的0处,对于每一个结点n,n的左孩子位于数组的2n+1处,右孩子位于2(n+1)处。
addElement- 该操作有三个步骤:
- 在适当位置处添加新结点,在这一步中,与链表实现不同,它不需要确定双亲的位置(因为对于结点n,其双亲的位置是固定的,位于数组的(n-1)/2处),所以时间复杂度为O(1)。
- 对于堆进行重新调整,该步的时间复杂度为O(logn)。
- 将count增加1,该步的时间复杂度为O(1)。
- 所以删除操作的时间复杂度为O(logn)。
- 在这个方法中应用了一个私有方法
heapifyAdd(在必要时,从该结点开始,对剩余堆进行重新调整直至根处)。
- 该操作有三个步骤:
removeMin- 该操作有三个步骤:
- 用堆中的最末结点替换根结点,该步的时间复杂度为O(1)。
- 在必要的情况下,对堆进行重新排序。这一步与其他方法中的调整排序类似,因此其时间复杂度为O(logn)。
- 返回初始的根元素,在数组中,根元素存储在数组的0处,所以这一步的时间复杂度为O(1)。
- 所以删除操作的时间复杂度为O(logn)。
- 在这个方法中应用了一个私有方法
heapifyRemove(在必要时,对下面的堆进行重新调整直至叶子结点)。
- 该操作有三个步骤:
四、堆的应用
(一)使用堆:优先级队列
- 虽然最小堆不是一个队列,但是它却提供了一个高效的优先级队列实现。
- 优先级队列:遵循两个排序规则的集合。
- 具有更高优先级的元素在先。
- 具有相同优先级的项目使用先进先出方法来确定其排序。
- 实现方法:实现方法:定义结点类保存队列中的元素、优先级和排列次序。然后,通过实现Comparable接口定义compareTo方法,先比较优先级,再比较排列次序。
(二)堆排序
- 堆排序由两部分构成:添加列表中的每个元素,然后一次删除一个元素。

- 时间复杂度分析:在插入操作中,每一个元素的插入操作(即使用
addElement方法)的时间复杂度为O(logn),因此n个结点的时间复杂度为O(nlogn)。在删除操作中,每一个元素的删除操作(即使用removeMin方法)的时间复杂度也为O(logn),因此删除n个结点的时间复杂度为O(nlogn)。所以堆排序的时间复杂度为O(nlogn)。 - 堆排序的过程
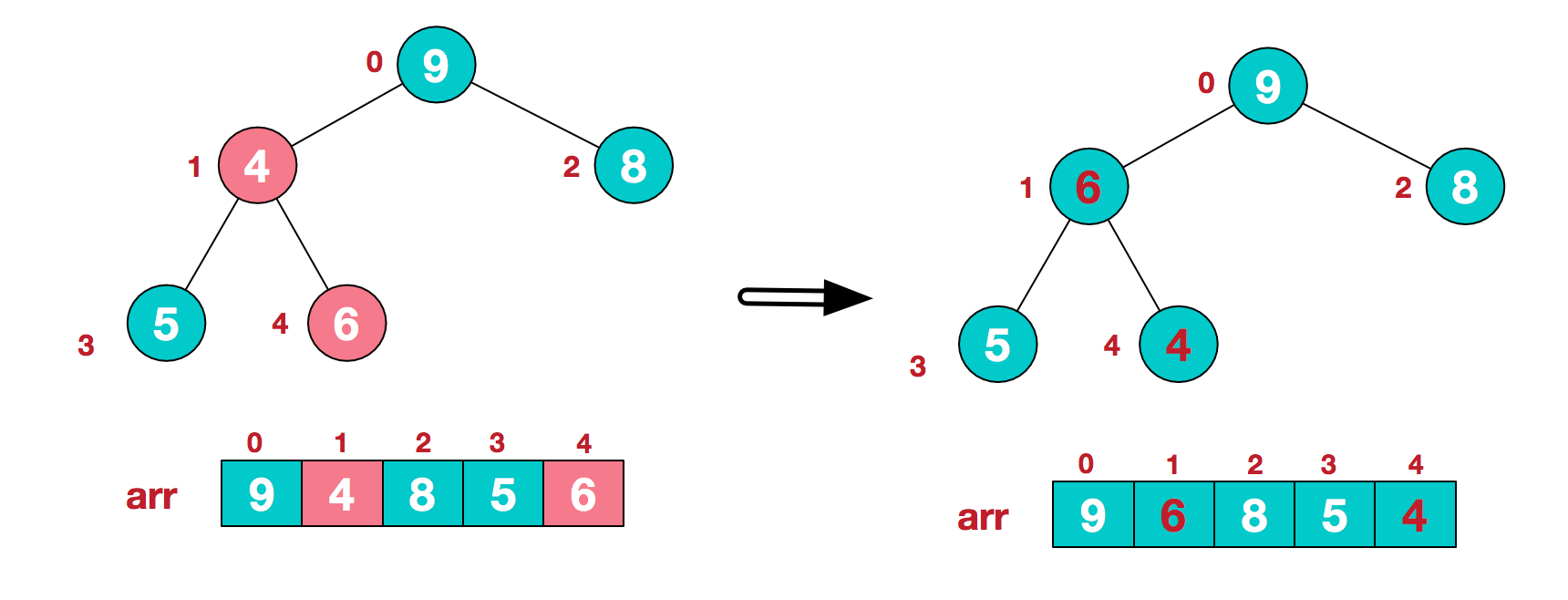
- 第一步:将根结点与最末结点交换,将新的最末结点输出,对剩余的树进行调整使之重新成为堆。如在下图中,将根结点
9与最末结点4进行交换,然后将9输出;对于剩下的部分,从新的根结点开始,4比它的左右孩子都小,因此与二者之间较大的8进行交换,交换后4变为叶子结点,开始进行下一步操作。
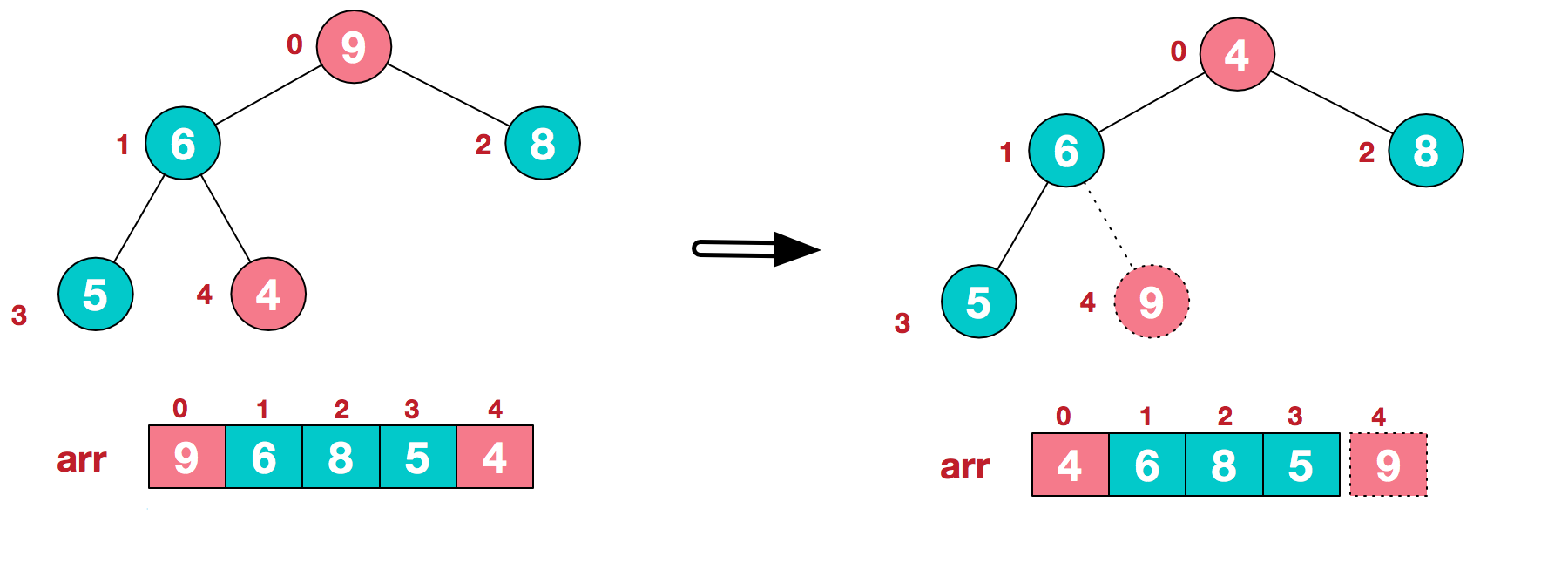
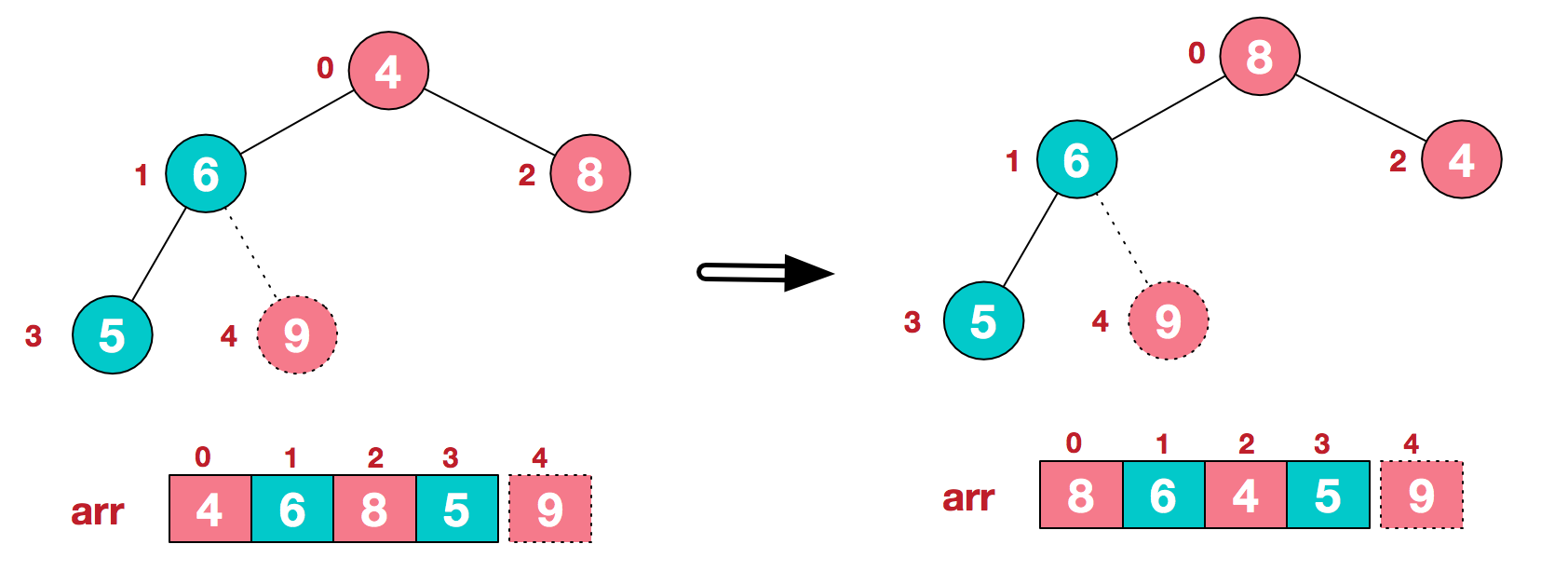
- 第二步:重复第一步的操作直至输出所有元素。
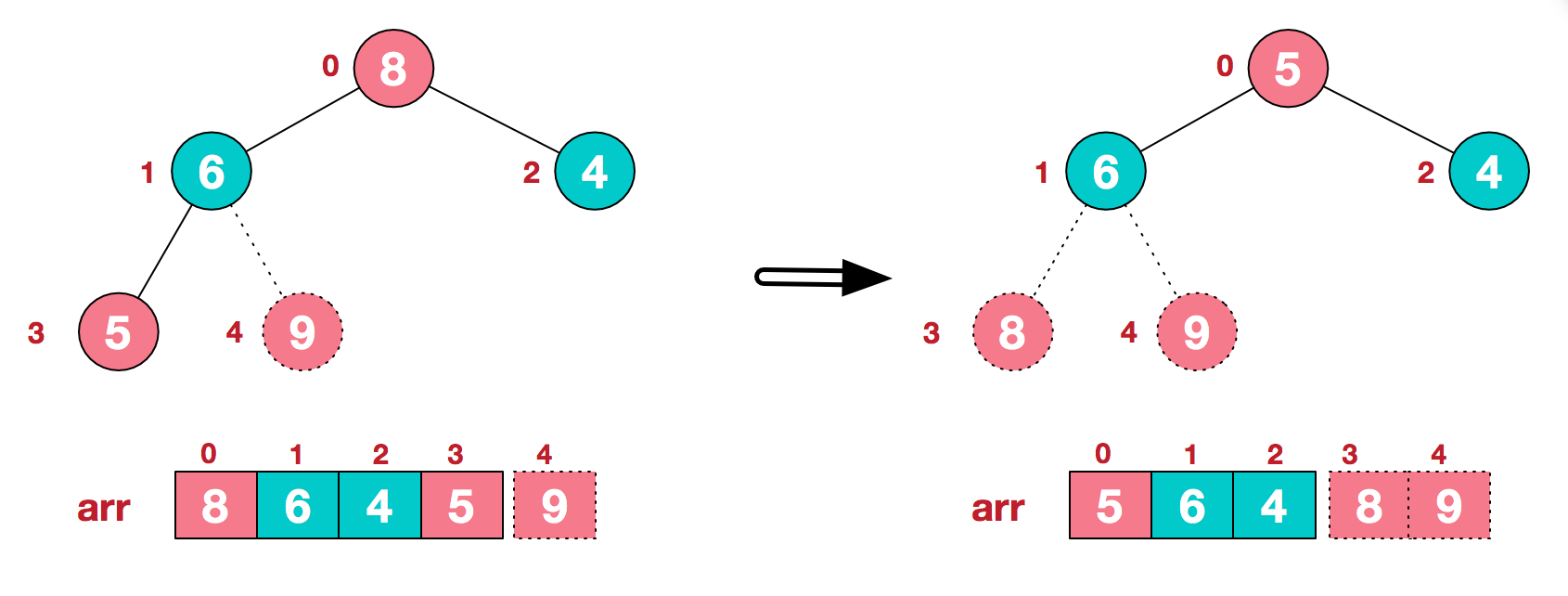
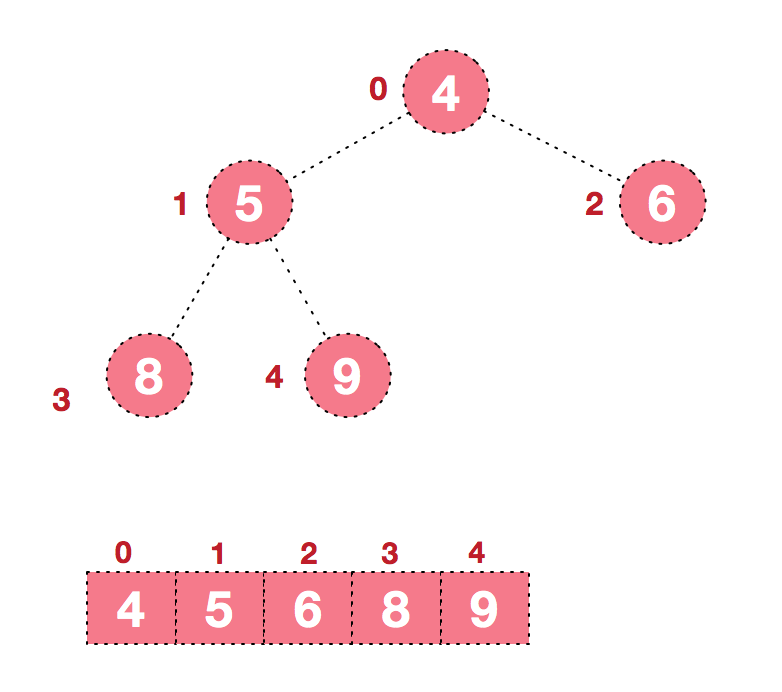
- 第一步:将根结点与最末结点交换,将新的最末结点输出,对剩余的树进行调整使之重新成为堆。如在下图中,将根结点
- 规律:使用大顶堆排序后生成的是升序排列,使用小顶堆排序后生成的是降序排列。
教材学习中的问题和解决过程
- 问题1:在查资料的过程中发现很多博客都喜欢把堆和栈放到一块来讲,感觉这两者并没有什么关联,但是为什么会把它们两个放在一起比较呢?
- 问题1解决方案:因为栈与堆都是Java用来在Ram中存放数据的地方。Java把内存划分成两种:一种是栈内存,一种是堆内存。所以栈和堆经常被放在一起比较。
- 栈内存:在函数中定义的一些基本类型的变量和对象的引用变量都在函数的栈内存中分配。 当在一段代码块定义一个变量时,Java就在栈中为这个变量分配内存空间,当超过变量的作用域后,Java会自动释放掉为该变量所分配的内存空间,该内存空间可以立即被另作他用。
- 堆内存:堆内存用来存放由new创建的对象和数组。
- 栈内存与堆内存的区别
- 堆内存用来存放由new创建的对象和数组,栈内存用来存放方法或者局部变量等。
- 堆是先进先出,后进后出;栈是后进先出,先进后出。
代码调试中的问题和解决过程
- 问题1:在实现PP12.1的时候,输出的结果并不是按照进入队列的顺序输出的。

- 问题1解决方法:当初张昊然同学和我讨论PP12.1时,我说应该不能直接用书上的优先级队列,因为它和队列还是有区别的,但是自己实现的时候虽然重新写了一个,但是感觉实际上还是实现了一个优先级队列。在查了相关资料之后,有一篇博客中写到说将生成的堆使用层序遍历就可以输出队列的结果了,原本我是使用
ArrayHeap类,为了查看堆的构造而改成了LinkedHeap类,但是从树的结构来看就算使用层序遍历它也依旧不是按照元素进入队列的顺序排列的。
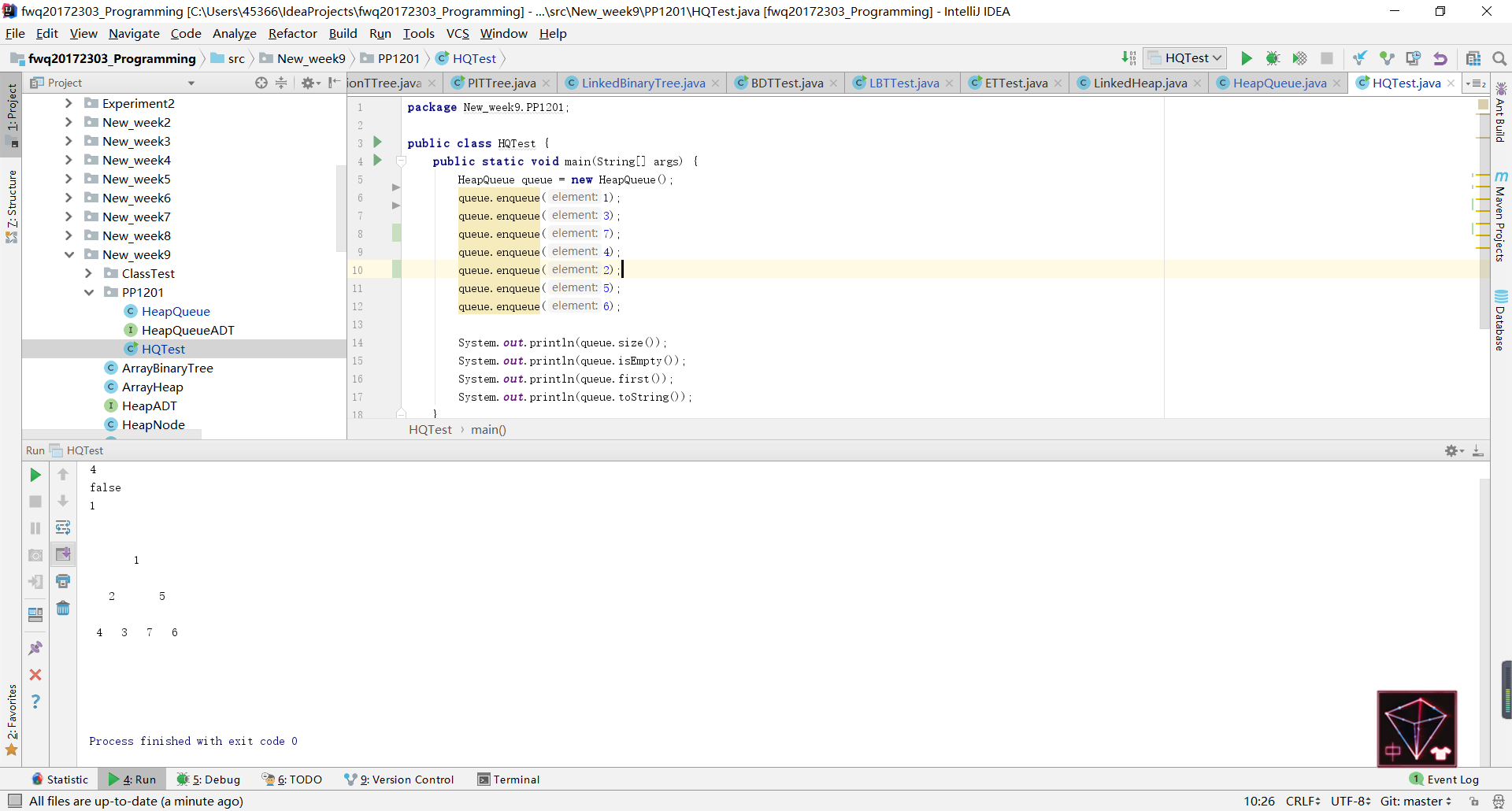
- 后来我又尝试了前序、中序和后序遍历,发现都不可以。
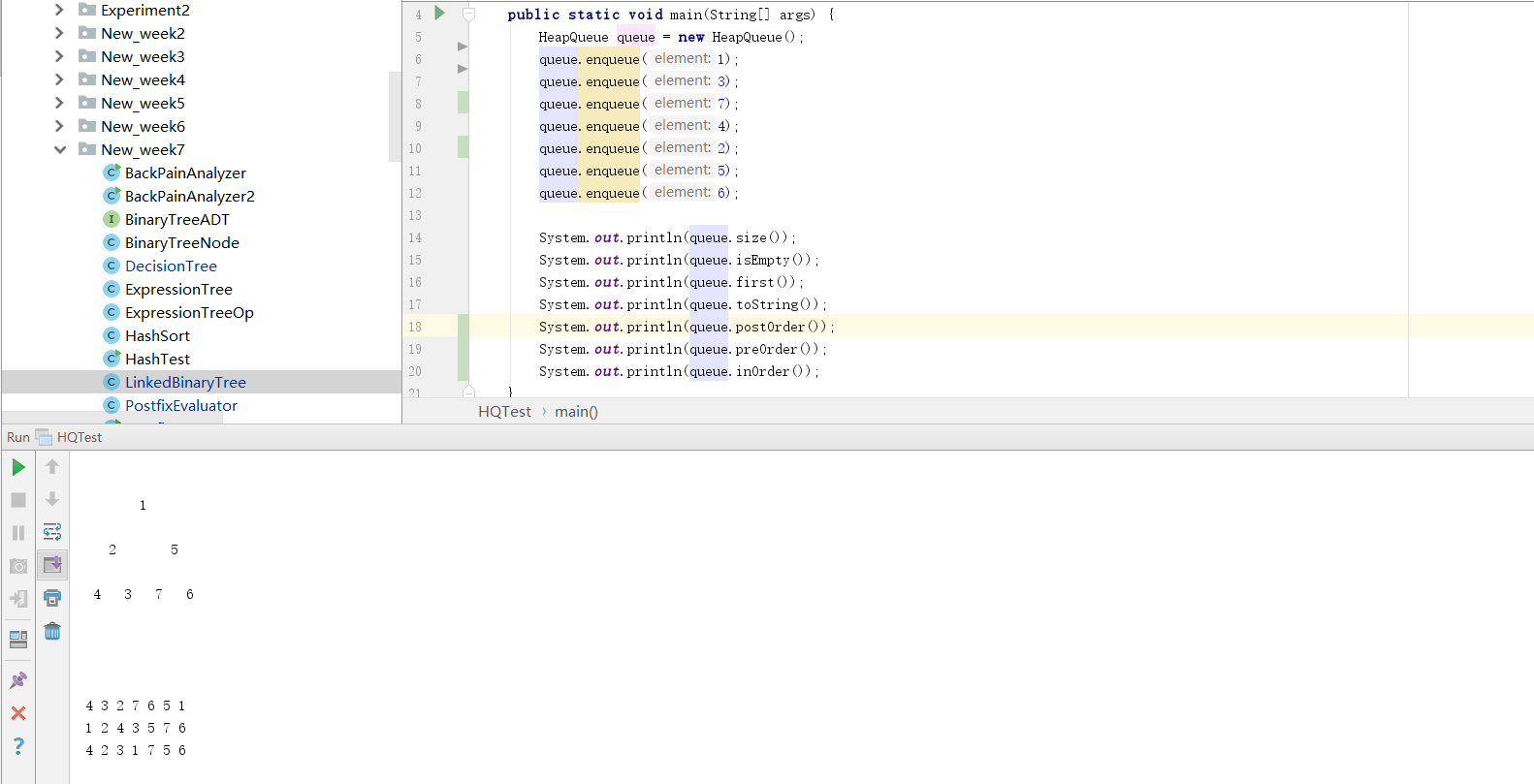
- 最后上网查了很多资料发现似乎用堆只能实现特殊的优先级队列,因为堆本身的性质就限制了它。
代码托管
- 上周代码量:15094

上周考试错题总结(正确为绿色,错误为红色)
- 错题1:Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
- A .True
- B .False
- 错题1解决方法:只关注了后面说的插入结点的位置的表述是否正确,忽略了前面的“二叉查找树”,原话说的是完全树,而二叉查找树并不都是完全树,所以这道题题干的表述是错误的。
- 错题2:The addElement operation for both the linked and array implementations is O(n log n).
- A .True
- B .False
- 错题2解决方法:添加方法的时间复杂度应该为O(logn),在上面的教材内容总结里已经详细分析过了。
结对及互评
点评模板:
- 博客中值得学习的或问题:
- 相比较之前而言博客的内容增加了对代码的理解,值得夸奖。但是对于在学习过程中遇到的问题记录还是有点草率,不过感觉本周的内容比较简单,确实不像之前会有那么多问题。
点评过的同学博客和代码
- 本周结对学习情况
- 20172322
- 结对学习内容
- 讨论了PP12.1的实现
其他(感悟、思考等,可选)
- 感觉本周的内容比较简单,代码方面课本上也给的很全很详细,所以这周的问题不是很多,写博客的时候找了很久才找到一个教材中遇到的问题。
- 本学期的课本内容也基本快学完了,很大的一个感触是本学期的博客质量整体而言要比上学期好,而且对课本内容的理解,对相关知识的应用也比上学期要进步了,希望能继续保持吧。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 10/10 | 1/1 | 10/10 | |
| 第二周 | 246/366 | 2/3 | 20/30 | |
| 第三周 | 567/903 | 1/4 | 10/40 | |
| 第四周 | 2346/3294 | 2/6 | 20/60 | |
| 第五周 | 2346/3294 | 2/8 | 30/90 | |
| 第六周 | 1343/4637 | 2/8 | 20/110 | |
| 第七周 | 654/5291 | 1/9 | 25/135 | |
| 第八周 | 2967/8258 | 1/10 | 15/150 |
- 计划学习时间:20小时
- 实际学习时间:15小时
- 改进情况:本来以为堆会很难,但发现比自己想象的要简单