1.Codeforces Edu Round 2. E. Lomsat gelral
题意:给你一棵树,树上有n个节点,每个节点有自己的颜色,让你求每个节点子树出现次数最多的颜色之和。
题解思路:利用轻重链剖分的特性去枚举每个节点,再用数组记录一下当前节点子树上每种颜色出现的次数,最后计算答案即可。
#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; #define ls l,mid,rt<<1 #define rs mid+1,r,rt<<1|1 const int MAXN = 1e5+10; const double EPS = 1e-12; const ll mod = 1e9+7; int n; int sz[MAXN],wson[MAXN],c[MAXN],csum[MAXN],b[MAXN]; ll ans[MAXN],maxx,COL; bool vis[MAXN]; vector<int>G[MAXN]; void dfs(int u,int fa){ sz[u]=1; for(auto v:G[u]){ if(v==fa)continue; dfs(v,u); sz[u]+=sz[v]; if(sz[v]>sz[wson[u]])wson[u]=v; } } void add(int u,int fa){ csum[c[u]]++; if(maxx<csum[c[u]])maxx=csum[c[u]],COL=c[u]; else if(maxx==csum[c[u]])COL+=c[u]; for(auto v:G[u]){ if(v==fa||vis[v])continue; add(v,u); } } void del(int u,int fa){ csum[c[u]]--; for(auto v:G[u]){ if(v==fa)continue; del(v,u); } } void DFS(int u,int fa,int ty){ for(auto v:G[u]){ if(v==fa||v==wson[u])continue; DFS(v,u,0); } if(wson[u])DFS(wson[u],u,1),vis[wson[u]]=1; add(u,fa); ans[u]=COL; vis[wson[u]]=0; if(ty==0)del(u,fa),maxx=0,COL=0; } void solve(int cas){ scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&c[i]); for(int i=1,u,v;i<n;i++){ scanf("%d %d",&u,&v); G[u].push_back(v); G[v].push_back(u); } dfs(1,0); DFS(1,0,1); for(int i=1;i<=n;i++)printf("%lld ",ans[i]); } int main() { int T=1; //scanf("%d",&T); for(int i=1;i<=T;i++)solve(i); }
2.2020 CCPC Wannafly Winter Camp Day2 E.阔力梯的树
题意:题目说的很清楚,自己看
题解思路:题目里只有对子树的询问,很显然是树上启发式合并,但由于中间有个排序过程,priority_queue不能中间插值,这里可以使用set来计算。注意,题目中不能等到把所有子树节点插入set后再进行求值(n^2logn显然会t),边插入就可以边计算了,注意消去前后影响就好。
#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; #define ls l,mid,rt<<1 #define rs mid+1,r,rt<<1|1 #define endl ' ' #define ps puts("###") const int MAXN = 1e5+10; const double EPS = 1e-12; const ll mod = 1e9+7; int n; int sz[MAXN],wson[MAXN],vis[MAXN]; ll ans[MAXN],sum; vector<int>G[MAXN]; set<int>s; void dfs(int u){ sz[u]=1;wson[u]=0; for(auto v:G[u]){ dfs(v); sz[u]+=sz[v]; if(sz[v]>sz[wson[u]])wson[u]=v; } } void add(int u){ s.insert(u); if(s.size()==1)return ; else{ auto it1=s.lower_bound(u),it2=s.upper_bound(u); if(it1==s.begin())sum+=1ll*(*it2-*it1)*(*it2-*it1); else if(it2==s.end()){ --it1; --it2; sum+=1ll*(*it2-*it1)*(*it2-*it1); } else { --it1; sum-=1ll*(*it2-*it1)*(*it2-*it1); --it2; sum+=1ll*(*it2-*it1)*(*it2-*it1); ++it1;++it2; sum+=1ll*(*it2-*it1)*(*it2-*it1); } } } void dfs3(int u){ add(u); for(auto v:G[u]){ if(!vis[v])dfs3(v); } } void dfs2(int u,int ty){ for(auto v:G[u]){ if(v!=wson[u])dfs2(v,0); } if(wson[u])dfs2(wson[u],1),vis[wson[u]]=1; dfs3(u); ans[u]=sum; vis[wson[u]]=0; if(!ty)s.clear(),sum=0; } void solve(int cas){ scanf("%d",&n); for(int i=2,fa;i<=n;i++){ scanf("%d",&fa); G[fa].push_back(i); } dfs(1);dfs2(1,1); for(int i=1;i<=n;i++)printf("%lld ",ans[i]); } int main() { int T=1; //scanf("%d",&T); for(int i=1;i<=T;i++)solve(i); }
题意:题目里说的很清楚
题解思路:很显然,这题是利用dsu on tree的优越性去枚举当前点作为lca点时符合条件的点对数量,那么怎么才能不重不漏地枚举呢?根据lca的特性,显然只有位于不同第一层子树下的点lca会在当前点上,这时我们可以利用map(或是可以离散一下)去对当前子树节点的每个值进行记录,能形成多少对其实就是sum1[x]*sum2[2 * root - x],其中,sum1代表的是当前子树每个值的数量,sum2代表的是其他子树每个值的数量,root代表当前枚举到作为lca的点。最后把ans*2即可(x,y位置互换)。
#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; #define ls l,mid,rt<<1 #define rs mid+1,r,rt<<1|1 #define endl ' ' #define ps puts("###") const int MAXN = 1e5+10; const double EPS = 1e-12; const ll mod = 1e9+7; int n; int a[MAXN],sz[MAXN],wson[MAXN],vis[MAXN]; ll ans; vector<int>G[MAXN]; map<int,int>mp; void dfs(int u,int fa){ sz[u]=1; for(auto v:G[u]){ if(v==fa)continue; dfs(v,u); sz[u]+=sz[v]; if(sz[v]>sz[wson[u]])wson[u]=v; } } void add(int u,int fa){ mp[a[u]]++; for(auto v:G[u]){ if(v==fa||vis[v])continue; add(v,u); } } void calc(int u,int fa,int rt){ if(2*a[rt]>a[u])ans+=mp[2*a[rt]-a[u]]; for(auto v:G[u]){ if(v==fa||vis[v])continue; calc(v,u,rt); } } void dfs2(int u,int fa,int ty){ for(auto v:G[u]){ if(v==fa||v==wson[u])continue; dfs2(v,u,0); } if(wson[u])dfs2(wson[u],u,1),vis[wson[u]]=1; for(auto v:G[u]){ if(v==fa||vis[v])continue; calc(v,u,u); add(v,u); } mp[a[u]]++; vis[wson[u]]=0; if(ty==0)mp.clear(); } void solve(int cas){ scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d",&a[i]); for(int i=1,u,v;i<n;i++){ scanf("%d %d",&u,&v); G[u].push_back(v); G[v].push_back(u); } dfs(1,0); dfs2(1,0,1); cout<<ans*2; } int main() { int T=1; //scanf("%d",&T); for(int i=1;i<=T;i++)solve(i); }
4.2020 CCPC 长春 F. Strange Memory
题意:给你一棵树,树上有n个节点,每个节点有自己的值,求以下式子的值
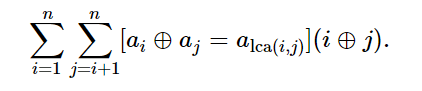
题解思路:和上一题一样,枚举每个点作为lca点,再去算答案,由于答案是a^b1+a^b2+...+a^bn的形式,注意a^b+a^c != a^(b+c),我们这里需要对b1、b2...bn进行拆位操作,用数组记录一下这个val对应的key每一位上有多少个0和1,最后统计答案时只需要把贡献都加起来就行了。(有一说一,轻重链剖分在不修改的情况下是真好用。)
#include<bits/stdc++.h> #include<tr1/unordered_map> using namespace std; typedef long long ll; typedef pair<int,int> PII; #define ls l,mid,rt<<1 #define rs mid+1,r,rt<<1|1 #define endl ' ' #define ps puts("###") const int MAXN = 1e5+10; const double EPS = 1e-12; const ll mod = 1e9+7; tr1::unordered_map<int,int>mp; int n,m; int a[MAXN],sz[MAXN],wson[MAXN],sum[MAXN][22][2]; ll ans; vector<int>G[MAXN]; void dfs1(int u,int fa){ sz[u]=1; for(auto v:G[u]){ if(v==fa)continue; dfs1(v,u); sz[u]+=sz[v]; if(sz[v]>sz[wson[u]])wson[u]=v; } } void calc(int u,int fa,int rt){ int x=a[u]^a[rt]; if(mp.count(x)){ int uu=u,now=0; while(now<22){ int xx=uu%2; ans+=1ll*sum[mp[x]][now][xx^1]*(1ll<<now); uu/=2; now++; } //cout<<"#######"<<u<<" "<<a[u]<<" "<<x<<" "<<a[rt]<<" "<<ans<<endl; } for(auto v:G[u]){ if(v==fa)continue; calc(v,u,rt); } } void update(int u,int fa,int val){ int uu=u,now=0; while(now<22){ int xx=uu%2; sum[mp[a[u]]][now][xx]+=val; uu/=2; now++; } for(auto v:G[u]){ if(v==fa)continue; update(v,u,val); } } void dfs2(int u,int fa,int ty){ for(auto v:G[u]){ if(v==fa||v==wson[u])continue; dfs2(v,u,0); } if(wson[u])dfs2(wson[u],u,1); for(auto v:G[u]){ if(v==fa||v==wson[u])continue; calc(v,u,u); update(v,u,1); } int uu=u,now=0; while(now<22){ int xx=uu%2; sum[mp[a[u]]][now][xx]++; uu/=2; now++; } if(ty==0)update(u,fa,-1); } int main() { scanf("%d",&n); int cnt=0; for(int i=1;i<=n;i++){ scanf("%d",&a[i]); if(!mp[a[i]])mp[a[i]]=++cnt; } for(int i=1,u,v;i<n;i++){ scanf("%d %d",&u,&v); G[u].push_back(v); G[v].push_back(u); } dfs1(1,0);dfs2(1,0,1); cout<<ans<<endl; }