Luogu P4299 首都

LCT维护重心

考虑合并两个树找重心

LCT维护子树SZ

法一：

暴力插入，启发式合并。每次插入一个考虑是否要把重心进行移动。条件是这条边的两边的子树sz哪个更大。相同则取编号小的。

O(Nlog^2N)不够优秀

法二：

找重心太暴力

两个树新的重心一定在重心相连的路径上。否则一定会有一个子树sz>sum/2

考虑对路径进行二分

怎么二分？

splay本身具有优秀的logn高度的性质，左右儿子则分别是链的向上和向下部分

决策重心与否唯一要考虑的是路径两大块是否sz<=sum/2都成立（其他小子树之前不影响，现在一定也不影响）

由于会排除一些区间，所以lsum=0，rsum=0来处理两大块已经排除过去的sz

把树立起来

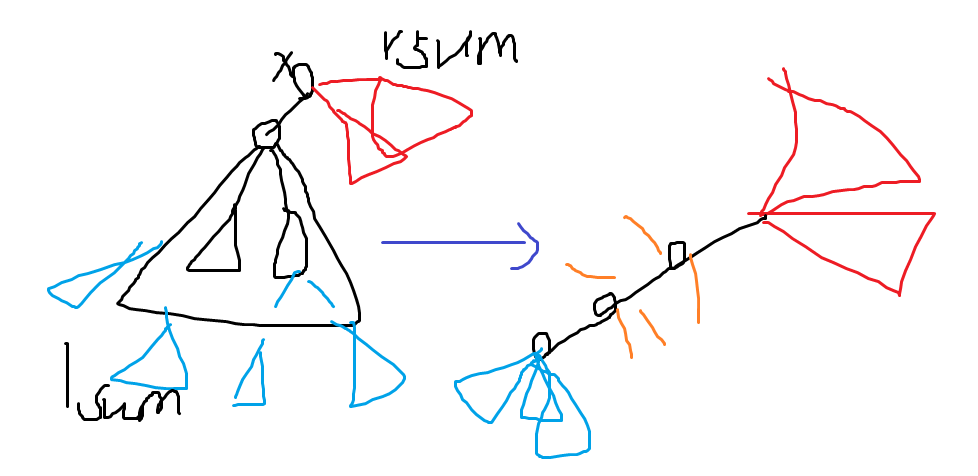
从x开始往下找。

只要考虑当前是否t[ls].sz+lsum<=sum/2&&t[rs].sz+rsum<=sum/2，是的话，就是一个重心。奇数点直接return，偶数点还要继续找（反正最多logn次）

 找t[].sz+[]sum较大的一个。并且较小的一半[^1]sum+=t[x].si+1+t[^1].sz（注意t[x].si，小的子树别忽略）

找到了叶子，一定找到了答案，返回即可。

可以外面再用并查集维护所在树的重心，方便快速查找。

注意：

1.t[x].si，小的子树别忽略

2.link(x,y)的时候，更新t[x].si,pushup(x)虚子树的sz加进来

3.upda的时候pushdown(x)（我也不知道为什么？？感觉之间access已经pushdown完了？？）

（upda：2019.3.13：显然不会pushdown完的。。。）

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define ls t[x].ch[0]
#define rs t[x].ch[1]
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5+5;
const int inf=0x3f3f3f3f;
int n,m;
struct node{
    int fa,ch[2];
    int s,si;
    int r;
}t[N];
int fa[N],rt[N],sz[N];
int xo;
int fin(int x){
    return fa[x]==x?x:fa[x]=fin(fa[x]);
}
bool nrt(int x){
    return (t[t[x].fa].ch[0]==x||t[t[x].fa].ch[1]==x);
}
void rev(int x){
    swap(ls,rs);
    t[x].r^=1;
}
void pushdown(int x){
    if(t[x].r){
        rev(ls);rev(rs);
        t[x].r=0;
    }
}
void pushup(int x){
    if(x) t[x].s=t[ls].s+t[rs].s+t[x].si+1;
}
void rotate(int x){
    int y=t[x].fa,d=t[y].ch[1]==x;
    t[t[y].ch[d]=t[x].ch[!d]].fa=y;
    if(nrt(y)) t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x;
    else t[x].fa=t[y].fa;
    t[t[x].ch[!d]=y].fa=x;
    pushup(y);
}
int sta[N];
void splay(int x){
    int y=x,z=0;
    sta[++z]=y;
    while(nrt(y)) y=t[y].fa,sta[++z]=y;
    while(z) pushdown(sta[z--]);
    
    while(nrt(x)){
        y=t[x].fa,z=t[y].fa;
        if(nrt(y)){
            rotate(((t[y].ch[0]==x)==(t[z].ch[0]==y)?y:x));
        }
        rotate(x);
    }
    pushup(x);
}
void access(int x){
    for(reg y=0;x;y=x,x=t[x].fa){
        splay(x);
        t[x].si+=t[t[x].ch[1]].s;
        t[x].si-=t[y].s;
        t[x].ch[1]=y;
        pushup(x);
    }
}
void makert(int x){
    access(x);splay(x);rev(x);
}
void split(int x,int y){
    makert(x);access(y);splay(y);
}
void link(int x,int y){
    split(x,y);
    t[x].fa=y;
    t[y].si+=t[x].s;pushup(y);
}
int upda(int x){//and find zhong
    int sum=t[x].s;
    int lsum=0,rsum=0;
    int id=inf;
    while(x){
        pushdown(x);
        if(t[rs].s+rsum<=sum/2&&t[ls].s+lsum<=sum/2){
            id=min(id,x);
            if(sum&1) break;
        }
        if(t[rs].s+rsum<t[ls].s+lsum){
            rsum+=t[x].si+t[rs].s+1;x=ls;
        }else{
            lsum+=t[x].si+t[ls].s+1;x=rs;
        }
    }
    splay(id);
    return id;
    //don't forget to upda fa[x],sz[x],rt[x]
    //don't forget to upda XOR
}
int main(){
    rd(n);rd(m);
    for(reg i=1;i<=n;++i) fa[i]=i,rt[i]=i,xo^=i,t[i].s=1,sz[i]=1;
    char s[10];
    int x,y;
    while(m--){
        scanf("%s",s+1);
        if(s[1]=='X'){
            printf("%d
",xo);
        }else if(s[1]=='A'){
            rd(x);rd(y);
            link(x,y);
            split(x=fin(x),y=fin(y));
            int z=upda(y);
            xo^=y^x^z;
            fa[x]=fa[y]=fa[z]=z;
        }else{
            rd(x);
            x=fin(x);
            printf("%d
",x);
        }
    }
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2018/12/27 15:32:41
*/

 总结：

splay上二分找重心的思路值得注意！

二分不光是mid=(l+r)>>1

线段树，平衡树logn树高的结构，也许都可以支持二分！（二分本质也是一棵树的一条链，不同之处是“线段树”那种二分树，本题是“平衡树”的那种）