每日一题_191209

若关于(x)的方程(dfrac{x}{mathrm{e}^x}+dfrac{mathrm{e}^x}{x+mathrm{e}^x}+m=0)有三个不相等的实数解(x_1,x_2,x_3),且(x_1<0<x_2<x_3),其中(minmathbb{R}),(mathrm{e})为自然对数的底数,则(left( dfrac{x_1}{mathrm{e}^{x_1}}+1 ight)^2left(dfrac{x_2}{mathrm{e}^{x_2}}+1 ight)left(dfrac{x_3}{mathrm{e}^{x_3}}+1 ight))的值为((qquad))
(mathrm{A}.1+m) (qquadmathrm{B}.mathrm{e}) (qquadmathrm{C}.m-1) (qquadmathrm{D}.1)
解析:
若记$$t(x)=dfrac{x}{mathrm{e}^x},t eq -1.$$则(t)的取值范围为(left(-infty,-1 ight)cupleft(-1,dfrac{1}{mathrm{e}} ight]),由题可得关于(t)的一元二次方程$$
t^2=-(1+m)(t+1),tinleft(-infty,-1 ight)cupleft(-1,dfrac{1}{mathrm{e}} ight].$$如下图绘制出二次函数(y=t^2)与(y=-(1+m)(t+1))的图象,由于关于(x)的方程有三个实数解,


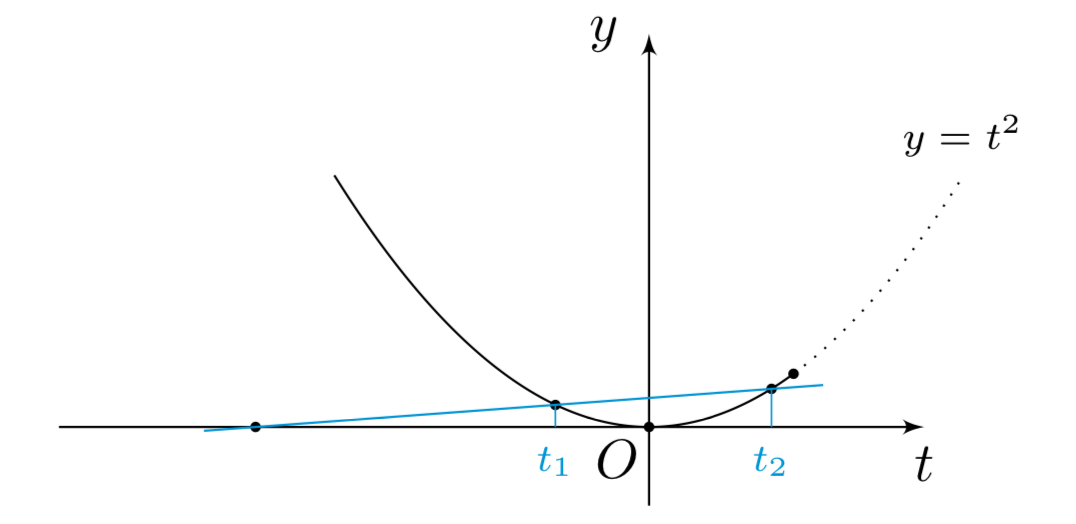
因此必然地关于$t$的一元二次方程在$left(-infty,-1 ight)cupleft(-1,dfrac{1}{mathrm{e}} ight]$上有两个异号的实根$t_1,t_2$,且满足$$ t_1<0

从而所求表达式为$$ (1+t_1)^2(1+t_2)^2=left[1+(t_1+t_2)+t_1t_2 ight]^2=1.$$