Test on 11/10/2018

杭电半日游，这新生赛出的题目比较简单，刚开始四十分钟写了三道题，并拿了一个一血，得到气球超开心。

可是后来就写不出来了，还是学的太少。

感觉还是有增长信心的，虽然感觉自己以前学过欺负他们，但是我也忘完了呀。

还是要努力啊QAQ

不要丧失希望，永远保持斗志，加油吧。

A：热烈的决斗者

Description

Jeff正在玩一种卡牌游戏，在这个游戏中，每个回合玩家可以执行以下两种操作无数次：

1.使用一张手上的牌。
2.命令场上的一只生物对敌方造成伤害，每一只生物在一个回合内最多攻击一次。

现在Jeff的场上拥有n只生物，第i只怪物拥有ai点攻击力与bi点血量。
同时，Jeff手上有m张手牌。由于他的运气实在太差了，他的所有手牌都只有一个功能——使场上一只生物的攻击力等于它的血量。

现在正是斩杀对手的关键回合，Jeff希望他能通过一种合理的策略，对敌方造成最高的伤害。请帮助Jeff计算他能造成的最高伤害。

Input

题目包含多组测试数据。
第一行是一个整数T，表示有T组测试数据。
对于每组测试数据，第一行包含两个整数n,m(0 <= n,m <= 500),表示场上生物数量和手牌数量。
接下来的n行，每行包含两个整数ai,bi(1 <= ai,bi <= 10000000),表示第i只怪物的攻击力和血量。

Output

输出Jeff在一个回合内能对敌方造成的最高伤害。

Examples

Input

1

3 2

1 3

2 4

5 3

Output

12

Hint

对于第一组样例： Jeff可以先对场上第1只和第2只生物使用手牌，使得它们的攻击力变成3和4。 然后Jeff命令所有生物攻击，总共可以造成12点伤害。

正确解法：

原本就是全部加a[i],把b[i]-a[i] 排序，取出前m个在加起来，不知道为什么wa

等待正解。

B:qw的表白

Description

qw喜欢上了一个美丽的女孩，并勇敢向她表白。但女神喜欢算法厉害的男生，便给他出了一道题：
给定包含n 个整数的数列a 和m 个询问，每个询问包含两个整数L ，R ，对于每一个询问，要求输出数列中有多少个数ai ，满足L≤a2i≤R ，即有多少个数平方后取值范围在[L,R] 之间。
单身二十年的qw非常想谈恋爱，你能帮帮他吗？ 

Input

多组数据。
第一行给出数据组数T（1≤T≤50 ）
每组数据首先给定两个整数n ,m ，表示数列中数的个数和询问个数。（1≤n,m≤50000 ）
随后一行给出n 个整数 a1,a2,a3...an （1≤ai≤1e9 ）
随后m 行，每行两个整数 L , R ，表示当前询问的数值范围区间。（1≤L≤R≤1e9 ）

Output

对于每个询问，单独输出一行，包含一个整数，表示数列中满足条件的数个数

Examples

Input

1

5 3

1 2 3 4 5

1 4

4 9

1 25

Output

2

2

5

正确解法：

我以为1e9 long long 会超，其实不会，那么就很简单

long long 排序，二分搜索。

写了半天二分搜索，后面发现可能有一个二分函数，有点sad，但无论学了什么都要保证自己会呀。

#include "pch.h"
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
int n, m;
long long a[50100],l,r;
long long upp(int n,long long r)
{
    int ll = 0, rr = n+1;
    while (ll+1 < rr)
    {
        int mid = (ll + rr) / 2;
        if (a[mid] <= r)    ll = mid;
        else rr = mid;
    }
    return rr;
}
long long downn(int n, long long l)
{
    int ll = 0, rr = n;
    while (ll + 1 < rr)
    {
        int mid = (ll + rr) / 2;
        if (a[mid] >= l)    rr = mid;
        else ll = mid;
    }
    return ll;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n >> m;
        memset(a, 0, sizeof(a));
        for (int i = 1; i <= n; i++)
        {
            cin >> a[i];
            a[i] = a[i] * a[i];
        }
        sort(a + 1, a + n + 1);
        for (int i = 1; i <= m; i++)
        {
            cin >> l >> r;
            cout << upp(n, r) - downn(n, l) - 1 << endl;
        }
    }
    return 0;
}

#include "pch.h"
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
int n, m;
long long a[50100],l,r;
long long upp(int n,long long r)
{
    int ll = 0, rr = n+1;
    while (ll+1 < rr)
    {
        int mid = (ll + rr) / 2;
        if (a[mid] <= r)    ll = mid;
        else rr = mid;
    }
    return rr;
}
long long downn(int n, long long l)
{
    int ll = 0, rr = n;
    while (ll + 1 < rr)
    {
        int mid = (ll + rr) / 2;
        if (a[mid] >= l)    rr = mid;
        else ll = mid;
    }
    return ll;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n >> m;
        memset(a, 0, sizeof(a));
        for (int i = 1; i <= n; i++)
        {
            cin >> a[i];
            a[i] = a[i] * a[i];
        }
        sort(a + 1, a + n + 1);
        for (int i = 1; i <= m; i++)
        {
            cin >> l >> r;
            cout << upper_bound(a+1,a+n+1,r)-lower_bound(a+1,a+n+1,l)<< endl;
        }
    }
    return 0;
}

C:Jeff与骰子游戏

Description

骰子大家一定都玩过。
一个骰子有六个面，每个面都有一个数字。对于骰子的每一个面，你都可以通过朝一个方向翻转90度来获得另一个面。

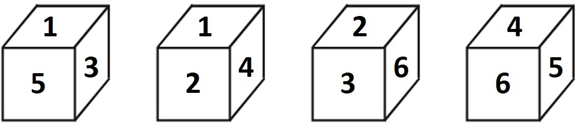
现在你有一个骰子，一开始朝上的一面点数为1（如图上的第一个骰子所示）。
你每次都可以将它朝一个方向翻转90度，并获得相当于翻转之后的骰子朝上一面的点数的分数。比如，现在骰子朝上的一面点数为1，你可以通过翻转使它朝上的一面变成3，并获得3分。

现在给出一个目标分数s，请问你至少需要翻转几次，使得你的分数刚好等于目标分数。

Input

题目包含多组测试数据。
第一行是一个整数T，表示有T组测试数据。
对于每组测试数据，只有一个正整数s,表示你需要达到的目标分数。(1 <= s <= 10000) 

Output

对于每组测试数据，输出达到目标分数至少需要翻转几次,如果无解请输出-1。

Examples

Input

2

5

10

Output

1 2

Hint

对于第二组样例: 你可以先翻转90度，使得骰子朝上的一面变为4，并获得4分。 之后你可以再翻转90度，使得骰子朝上的一面变为6，并获得6分。 所以你至少需要2步来达到目标分数。

正确解法：

考试时觉得，每次骰子上面的数不确定，它能翻转到达的数也不确定，要一个一个判断，我觉得很麻烦，不会写，但其实只要不是它本身，和底下的数 7-i  其他的数都可以到达。

于是就成了一个裸bfs。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int book[100100];
struct student
{
    int shu, ci,daa;
}que[500100];
int bfs(int n)
{
    if (n == 1)    return 0;
    memset(book, 0, sizeof(book));
    memset(que, 0, sizeof(que));
    int head = 1, tail = 2;
    que[head].shu = 1;
    que[head].ci = 0;
    que[head].daa = 0;
    book[0] = 1;
    while (head < tail)
    {
        if (que[head].daa == n)    return que[head].ci;
        for (int i = 1; i <= 6; i++)
        {
            if (que[head].shu == i || que[head].shu == 7 - i)
                continue;
            if (book[que[head].daa+i] == 0)
            {
                que[tail].shu = i;
                que[tail].ci = que[head].ci + 1;
                que[tail].daa = que[head].daa + i;
                book[que[tail].daa] = 1;
                if (que[tail].daa == n)    return que[tail].ci;
                tail++;
            }
        }
        head++;
    }
    return -1;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n;
        cout << bfs(n) << endl;
    }
    return 0;
}

我是傻逼，现在觉得这题都好简单。为什么写不出来！

 

D:Rabbit寻宝记(2)

Description

Rabbit成功地打开了大门后，没多久就见到了梦寐以求的宝藏。里面的宝石种类共有N 种，每一种都有一个体积v 和它的价值val 。(已知第i 种宝石的体积为i ,编号从1 ~N )更让Rabbit兴奋的是，每种宝石的数量还是无穷无尽的。
Rabbit当然想把所有宝石全都带回家，但是她带的袋子却最多只能装下总体积为V 的宝石，所以贪心的Rabbit决定要带走总体积恰好为V 的宝石。
现在她突然想知道自己在拿走宝石数量恰好为N 的情况下总价值最大为多少？

Input

输入数据第一行是一个正整数T ，表示数据组数。(T<=20 )
每组数据占两行。
第一行为两个整数N，V 。(0<N<=1000，N<=V<=min(N∗N，2∗N) )
接下来一行有N个整数，代表N种宝石的价值vali 。(0<vali<=10000 )

Output

每组测试数据输出一行，代表在满足拿走宝石总体积恰为V 和数量恰好为N 的情况下Rabbit能拿走宝石的最大总价值。

Examples

Input

1

3 5

6 2 4

Output

16

正确解法：

动态规划QAQ不会

二维的多重背包，就是多加一维然后从0开始

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<map>
using namespace std;
int n,V,w[2010],v[1010];
int f[2010][1010];
int main()
{
    scanf("%d %d",&n,&V);
    for(int i=1;i<=n;i++)
    {
        w[i]=i;
        scanf("%d",&v[i]);
    }
    memset(f,-9999,sizeof(f));
    f[0][0]=0;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=V;j++)
            for(int k=1;k<=n;k++)
            {
                if(j>=w[i])
                f[j][k]=max(f[j][k],f[j-w[i]][k-1]+v[i]);
            }
    printf("%d
",f[V][n]);
    return 0;
}

（忘了多组测试2333）