
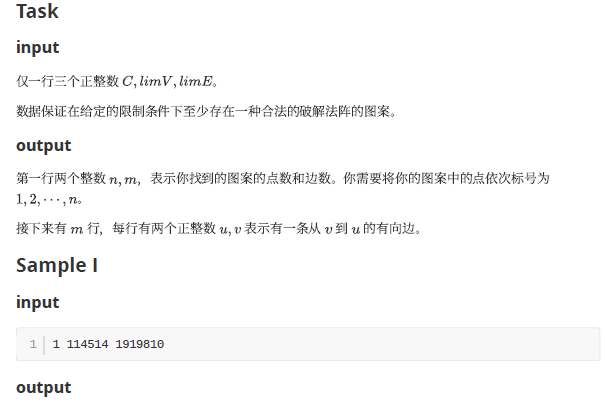
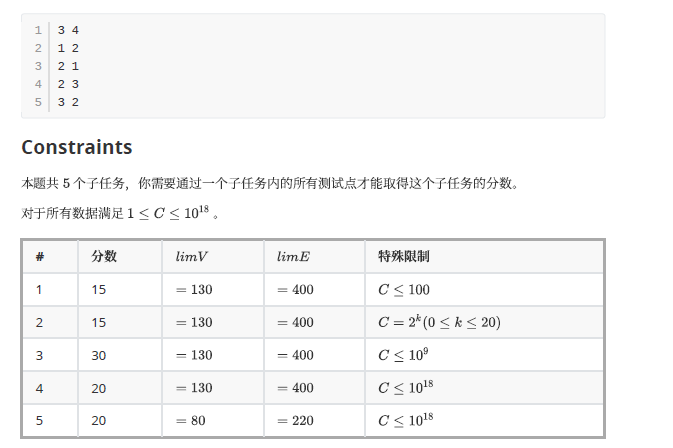
分析:
很离谱的构造题
第一个点直接输出C条重边就可以了
第二个点增加\(k\)个点,每个点向终点连2条边
其实第二个点给了我们一些提示,让我们向二进制之类的方向思考问题
考虑构造一个像这样的环
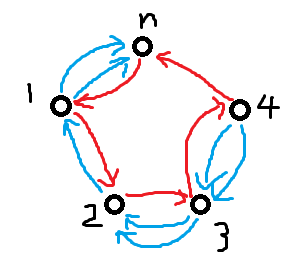
我们算一下方案,其实可以枚举断掉那条边,两端各自沿着红蓝边走向根
答案是\(2^0+2^1+2^1+2^2+2^3=17\)
我们把环的最后断开,看作一条链,假设有2条边的位置的值为1,否则为0
\(A={0,1,0,1,1}\)
求个前缀和:
\(S={0,1,1,2,3}\)
发现就是上面答案的指数
我们把\(C\)的二进制写出来,用前缀和的方式构造出一个环,就可以解决了
发现环的大小是\(O(2logC)\)级别的,在某些数据下,无法通过最后一个点
(然而数据很水,可以通过
看看正解:
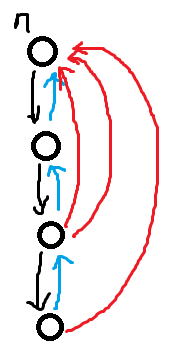

他的\(g\)想表达的是,如果选择的方案出现的不连通,在最后一个点接一条到\(n\)的红边就能够连通的方案数
剩下的推理都没有问题,不过这个随机有点神仙(
(可能这就是人类智慧吧
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define maxn 100005
using namespace std;
inline long long getint()
{
long long num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
long long C;
int n,m;
int a[maxn],cnt,sum;
inline long long gcd(long long p,long long q)
{return q?gcd(q,p%q):p;}
inline long long getrand(long long x,long long p,long long C)
{return ((x*x+p)%C+C)%C;}
int main()
{
srand(114514);
C=getint(),n=getint(),m=getint();
if(C<=100)
{
printf("2 %lld\n",C);
while(C--)printf("2 1\n");
return 0;
}
while(1)
{
long long x=rand();
do{x=getrand(x,rand(),C);}while(gcd(C,x)>1);
sum=cnt=0;
long long f=C,g=x;
while(1)
{
if(g==1){sum+=(a[++cnt]=f-1);break;}
sum+=(a[++cnt]=f/g),f%=g,g-=f;
if(cnt+1>n||sum+cnt*2>m)break;
}
if(cnt+1>n||sum+cnt*2>m)continue;
printf("%d %d\n",cnt+1,sum+cnt*2);
for(int i=1;i<=cnt;i++)
{
while(a[i]--)printf("%d %d\n",cnt+1,i);
printf("%d %d\n",i+1,i);
printf("%d %d\n",i,i+1);
}
return 0;
}
}
