拉格朗日对偶
对偶是最优化方法里的一种方法,它将一个最优化问题转换成另外一个问题,二者是等价的。拉格朗日对偶是其中的典型例子。对于如下带等式约束和不等式约束的优化问题:
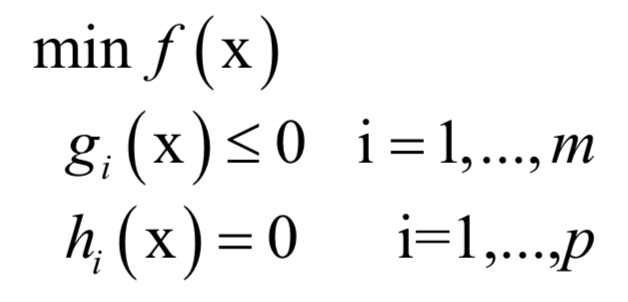
与拉格朗日乘数法类似,构造广义拉格朗日函数:
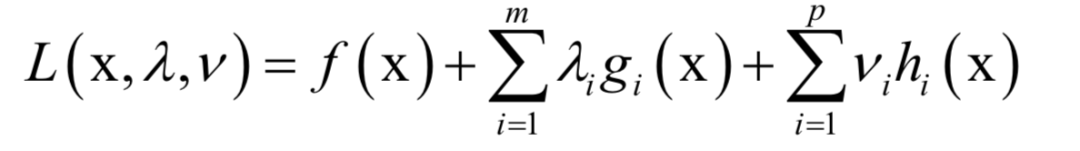
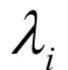 必须满足
必须满足 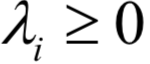 的约束。
的约束。
原问题为:
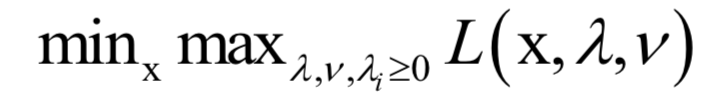
即先固定住x,调整拉格朗日乘子变量,让函数L取极大值;然后控制变量x,让目标函数取极小值。原问题与我们要优化的原始问题是等价的。
对偶问题为:
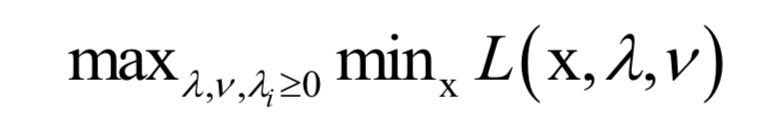
和原问题相反,这里是先控制变量x,让函数L取极小值;然后控制拉格朗日乘子变量,让函数取极大值。
一般情况下,原问题的最优解大于等于对偶问题的最优解,这称为弱对偶。在某些情况下,原问题的最优解和对偶问题的最优解相等,这称为强对偶。
强对偶成立的一种条件是Slater条件:一个凸优化问题如果存在一个候选x使得所有不等式约束都是严格满足的,即对于所有的i都有gi (x)<0,不等式不取等号,则强对偶成立,原问题与对偶问题等价。注意,Slater条件是强对偶成立的充分条件而非必要条件。
拉格朗日对偶在机器学习中的典型应用是支持向量机。