To avoid unsightly burns while tanning, each of the C (1 ≤ C ≤ 2500) cows must cover her hide with sunscreen when they're at the beach. Cow i has a minimum and maximum SPF rating (1 ≤ minSPFi ≤ 1,000; minSPFi ≤ maxSPFi ≤ 1,000) that will work. If the SPF rating is too low, the cow suffers sunburn; if the SPF rating is too high, the cow doesn't tan at all........
The cows have a picnic basket with L (1 ≤ L ≤ 2500) bottles of sunscreen lotion, each bottle i with an SPF rating SPFi (1 ≤ SPFi ≤ 1,000). Lotion bottle i can cover coveri cows with lotion. A cow may lotion from only one bottle.
What is the maximum number of cows that can protect themselves while tanning given the available lotions?
Input
* Line 1: Two space-separated integers: C and L
* Lines 2..C+1: Line i describes cow i's lotion requires with two integers: minSPFi and maxSPFi
* Lines C+2..C+L+1: Line i+C+1 describes a sunscreen lotion bottle i with space-separated integers: SPFi and coveri
Output
A single line with an integer that is the maximum number of cows that can be protected while tanning
Sample Input
3 2 3 10 2 5 1 5 6 2 4 1
Sample Output
2
题意:有C头牛,每个牛都有对阳光的承受空间【minspf,maxspf】,有L种防晒霜,每种都有SPF值和瓶数,涂到牛身上可使其只收到SPF值的阳光,每瓶只可涂一头牛,问最多几只牛可以享受阳光?
思路:
此题可以看成在一个数轴上操作。
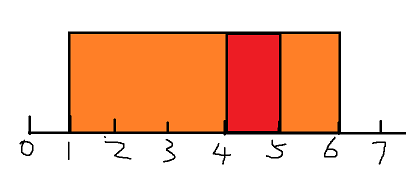
图中矩形块就代表了牛的承受区间,我们从左到右对牛进行涂防晒霜处理,可以从图中看到,
①【0,1】位置,无牛需要防晒霜
②【1,4】位置,只有一头牛有需求,那我们直接给橙色涂
④【4,5】位置,红色牛和橙色牛都有需求,给哪只牛涂呢?
有人可能说了,前面都给橙色牛涂了,现在肯定给红色啦,对,但是如果在【4,5】之前没有防晒霜呢(就一瓶防晒霜在【4,5】位置),也就是说这瓶防晒霜面临两个选择,
我们从图中看出,那肯定也是给红色牛啦,因为红色牛快承受不住啦(该牛承受区间右边界小),也就是说再往下进行的话,马上就出了红牛的承受区间了,然而橙牛却还没有,
所以我们先给红牛,之后再瞅瞅有没有适合橙牛的。
这样就可以看出我们的策略:
①将牛按右边界从小到大排序,防晒霜按spf从小到大排序
②将牛按左边界从大到小排序,防晒霜按spf从大到小排序
回头看这问题,对于排好序的牛(假设按①方式),有两瓶防晒霜x>y,那么是选x的,因为x,y对于后面的牛来说有三种情况,
①x、y可选
②x不可选,y可选
③x、y不可选(由左边界影响)
那么我们选择小的就对后面的牛来说影响最小
并且因为选择了对后面牛最小的影响方式,该牛可以选择防晒霜,就没有必要留给下头牛,因为只算牛头数,哪头牛不是牛呢

1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 using namespace std; 5 6 int C,L; 7 8 struct Node 9 { 10 int l; 11 int r; 12 } cow[3000],sun[3000]; 13 14 bool cmp1(Node a,Node b) 15 { 16 return a.l < b.l; 17 } 18 bool cmp2(Node a,Node b) 19 { 20 return a.r < b.r; 21 } 22 23 int main() 24 { 25 scanf("%d%d",&C,&L); 26 for(int i=1; i<=C; i++) 27 { 28 scanf("%d%d",&cow[i].l,&cow[i].r); 29 } 30 for(int i=1; i<=L; i++) 31 { 32 scanf("%d%d",&sun[i].l,&sun[i].r); 33 } 34 sort(cow+1,cow+1+C,cmp2); 35 sort(sun+1,sun+1+L,cmp1); 36 int ans = 0; 37 for(int i=1; i<=C; i++) 38 { 39 for(int j=1; j<=L; j++) 40 { 41 if(cow[i].l <= sun[j].l && cow[i].r >= sun[j].l && sun[j].r) 42 { 43 ans++; 44 sun[j].r--; 45 break; 46 } 47 } 48 } 49 printf("%d ",ans); 50 }
优先队列写法:

1 #include<bits/stdc++.h> 2 using namespace std; 3 4 int C,L; 5 struct Node 6 { 7 int l; 8 int r; 9 bool operator<(Node b) 10 { 11 return l < b.l; 12 } 13 } cow[3000],sun[3000]; 14 priority_queue<int,vector<int>,greater<int> >que; 15 int main() 16 { 17 scanf("%d%d",&C,&L); 18 for(int i=1; i<=C; i++) 19 scanf("%d%d",&cow[i].l,&cow[i].r); 20 for(int i=1; i<=L; i++) 21 scanf("%d%d",&sun[i].l,&sun[i].r); 22 sort(cow+1,cow+1+C); 23 sort(sun+1,sun+1+L); 24 int j = 1; 25 int ans = 0; 26 for(int i=1; i<=L; i++) 27 { 28 while(j<=C&&cow[j].l <= sun[i].l) 29 que.push(cow[j].r),j++; 30 while(!que.empty() && sun[i].r) 31 { 32 int tmp = que.top(); 33 que.pop(); 34 if(tmp >= sun[i].l) 35 ans++,sun[i].r--; 36 } 37 } 38 printf("%d ",ans); 39 }
