

之前我们已经了解了Coss Function的定义,它是一个convex,所以我们能找到它的全局最优解,我们可以先可以先随便选取一组w,b,求得刚开始J(w,b)对w的偏导,用公式:
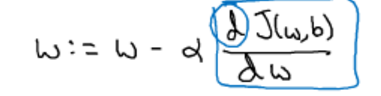 我们可以对w进行更新,其中α为学习率,为梯度下降的步长,α越大,步长越大,同理也可以对b更新,最后经过一步步迭代,我们能够找到最优解使得Cost Function最小.
我们可以对w进行更新,其中α为学习率,为梯度下降的步长,α越大,步长越大,同理也可以对b更新,最后经过一步步迭代,我们能够找到最优解使得Cost Function最小.
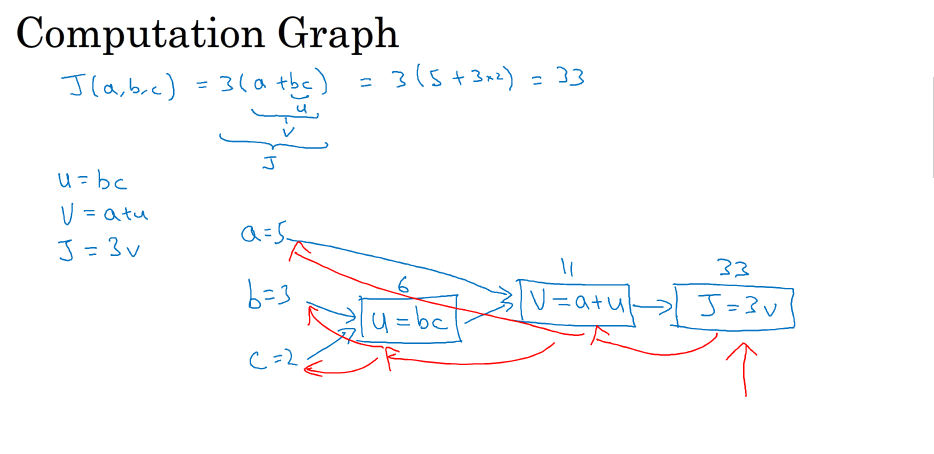
逻辑回归中包含了正向传播和反向传播,用一个计算图来表示其过程
计算图:
举一个简单的例子例:
把j(a,b,c)看作logistic回归成本函数j=3(a+bc),它的计算过程为让u=bc,v=a+u 得j=3v
其中正向传播为从左到右得到成本函数的过程
反向传播为对其进行求导得到dJ/da,dJ/db,dJ/dc
现在对一个逻辑回归进行梯度计算:
给定的逻辑回归中,Loss Function 表达式如下:
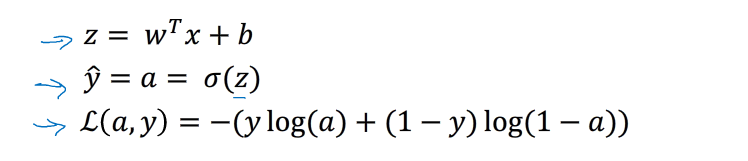
对于正向传播非常简单,假设输入样本x有两个特征值(x1,x2)则对应的w为w1,w2,则对应的最后的Loss Fuction如下:
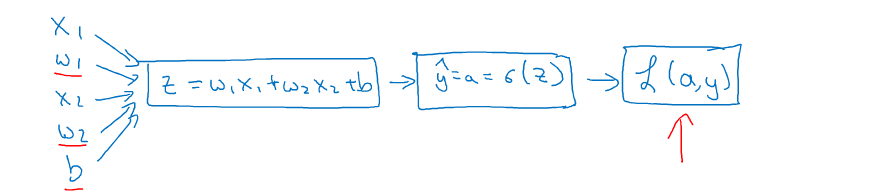
对于反向传播计算如下:
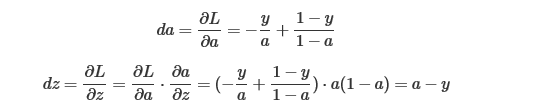
得到dz以后就可以对w1,w2进行求导了
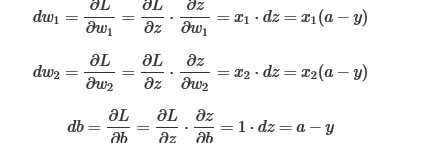
则梯度下降算法为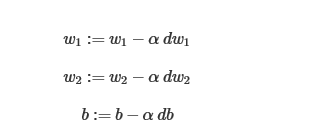
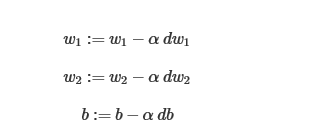
上述表示的是单个样本的logistic回归,对于多个样本的logistic回归表示如下:
Cost Function为:

假设该logistic回归有两个特征值,那么dw1,dw2,db表示如下:
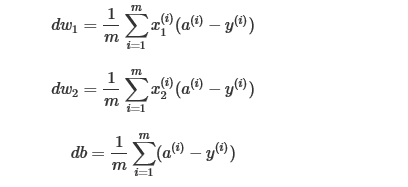
算法流程图如下:
J=0; dw1=0; dw2=0; db=0; //对w1,w2,b,以及J初始化
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J /= m;
dw1 /= m;
dw2 /= m;
db /= m;
完成上述算法即完成了一次迭代,通过公式:
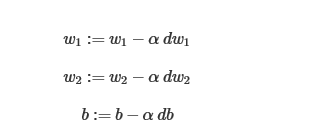
对其进行更新,这样经过多次迭代后,就能得出最优解