网络结构
概述
前几节我们尝试使用与房价预测相同的简单神经网络解决手写数字识别问题,但是效果并不理想。原因是手写数字识别的输入是28 × 28的像素值,输出是0-9的数字标签,而线性回归模型无法捕捉二维图像数据中蕴含的复杂信息,如 图1 所示。无论是牛顿第二定律任务,还是房价预测任务,输入特征和输出预测值之间的关系均可以使用“直线”刻画(使用线性方程来表达)。但手写数字识别任务的输入像素和输出数字标签之间的关系显然不是线性的,甚至这个关系复杂到我们靠人脑难以直观理解的程度。
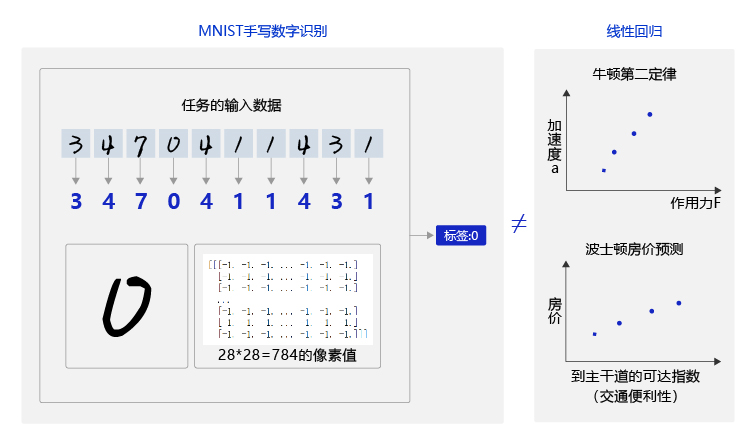
图1:数字识别任务的输入和输入不是线性关系
因此,我们需要尝试使用其他更复杂、更强大的网络来构建手写数字识别任务,观察一下训练效果,即将“横纵式”教学法从横向展开,如 图2 所示。本节主要介绍两种常见的网络结构:经典的多层全连接神经网络和卷积神经网络。
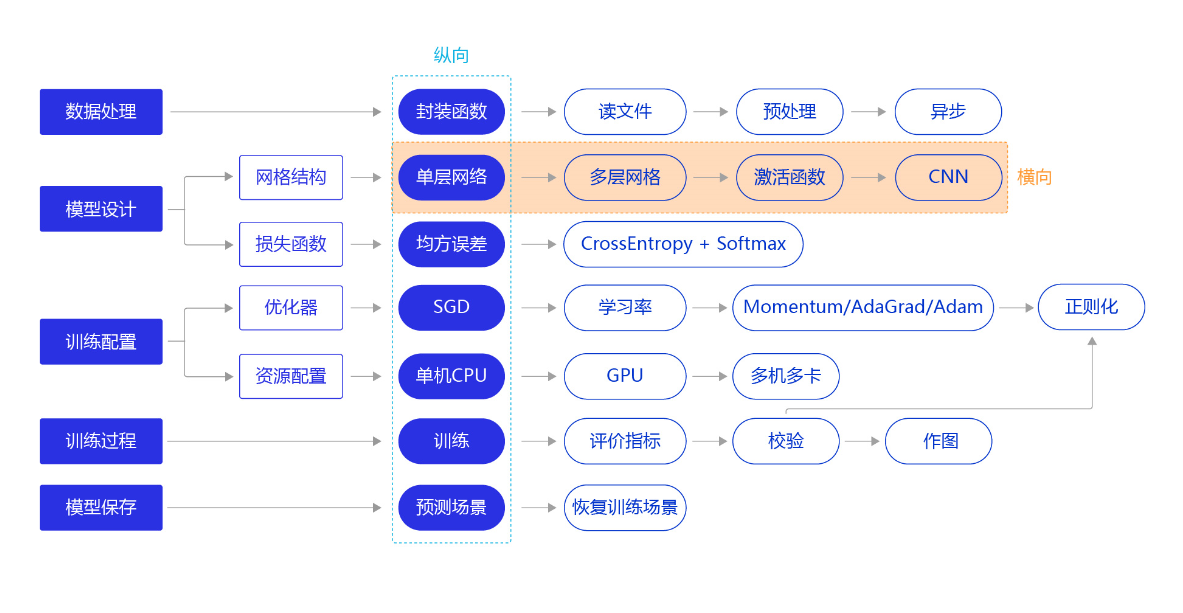
图2:“横纵式”教学法 — 网络结构优化
全连接神经网络与卷积神经网络
经典的全连接神经网络
经典的全连接神经网络来包含四层网络:输入层、两个隐含层和输出层,将手写数字识别任务通过全连接神经网络表示,如 图3 所示。
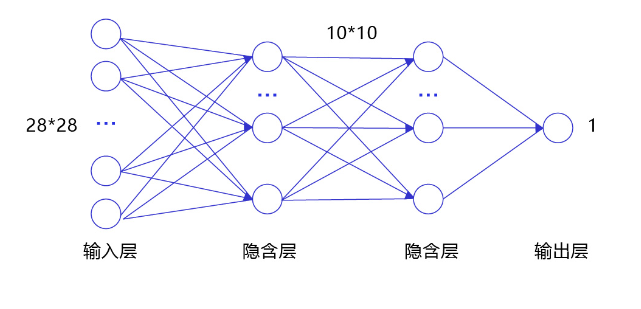
图3:手写数字识别任务的全连接神经网络结构
- 输入层:将数据输入给神经网络。在该任务中,输入层的尺度为28×28的像素值。
- 隐含层:增加网络深度和复杂度,隐含层的节点数是可以调整的,节点数越多,神经网络表示能力越强,参数量也会增加。在该任务中,中间的两个隐含层为10×10的结构,通常隐含层会比输入层的尺寸小,以便对关键信息做抽象,激活函数使用常见的sigmoid函数。
- 输出层:输出网络计算结果,输出层的节点数是固定的。如果是回归问题,节点数量为需要回归的数字数量。如果是分类问题,则是分类标签的数量。在该任务中,模型的输出是回归一个数字,输出层的尺寸为1。
说明:
隐含层引入非线性激活函数sigmoid是为了增加神经网络的非线性能力。
举例来说,如果一个神经网络采用线性变换,有四个输入(x_1)~(x_4),一个输出(y)。假设第一层的变换是(z_1=x_1-x_2)和(z_2=x_3+x_4),第二层的变换是(y=z_1+z_2),则将两层的变换展开后得到(y=x_1-x_2+x_3+x_4)。也就是说,无论中间累积了多少层线性变换,原始输入和最终输出之间依然是线性关系。
Sigmoid是早期神经网络模型中常见的非线性变换函数,公式为(Sigmoid(x) = frac {1}{1-e^{-x}}),通过如下代码,绘制出Sigmoid的函数曲线。如图4所示。
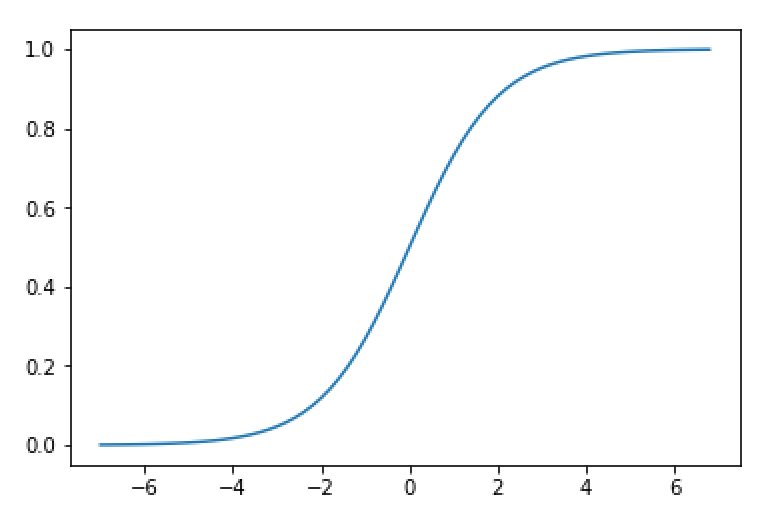
图4:sigmoid函数曲线
- 输入层的尺度为28×28,但批次计算的时候会统一加1个维度(大小为batchsize)。
- 中间的两个隐含层为10×10的结构,激活函数使用常见的sigmoid函数。
- 与房价预测模型一样,模型的输出是回归一个数字,输出层的尺寸设置成1。
下述代码为经典全连接神经网络的实现。完成网络结构定义后,即可训练神经网络。
# 多层全连接神经网络实现
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义两层全连接隐含层,输出维度是10,激活函数为sigmoid
self.fc1 = Linear(input_dim=784, output_dim=10, act='sigmoid') # 隐含层节点为10,可根据任务调整
self.fc2 = Linear(input_dim=10, output_dim=10, act='sigmoid')
# 定义一层全连接输出层,输出维度是1,不使用激活函数
self.fc3 = Linear(input_dim=10, output_dim=1, act=None)
# 定义网络的前向计算
def forward(self, inputs, label=None):
inputs = fluid.layers.reshape(inputs, [inputs.shape[0], 784])
outputs1 = self.fc1(inputs)
outputs2 = self.fc2(outputs1)
outputs_final = self.fc3(outputs2)
return outputs_final
卷积神经网络
虽然使用经典的全连接神经网络可以提升一定的准确率,但对于计算机视觉问题,效果最好的模型仍然是卷积神经网络。卷积神经网络针对视觉问题的特点进行了网络结构优化,更适合处理视觉问题。
卷积神经网络由多个卷积层和池化层组成,如 图4 所示。卷积层负责对输入进行扫描以生成更抽象的特征表示,池化层对这些特征表示进行过滤,保留最关键的特征信息。
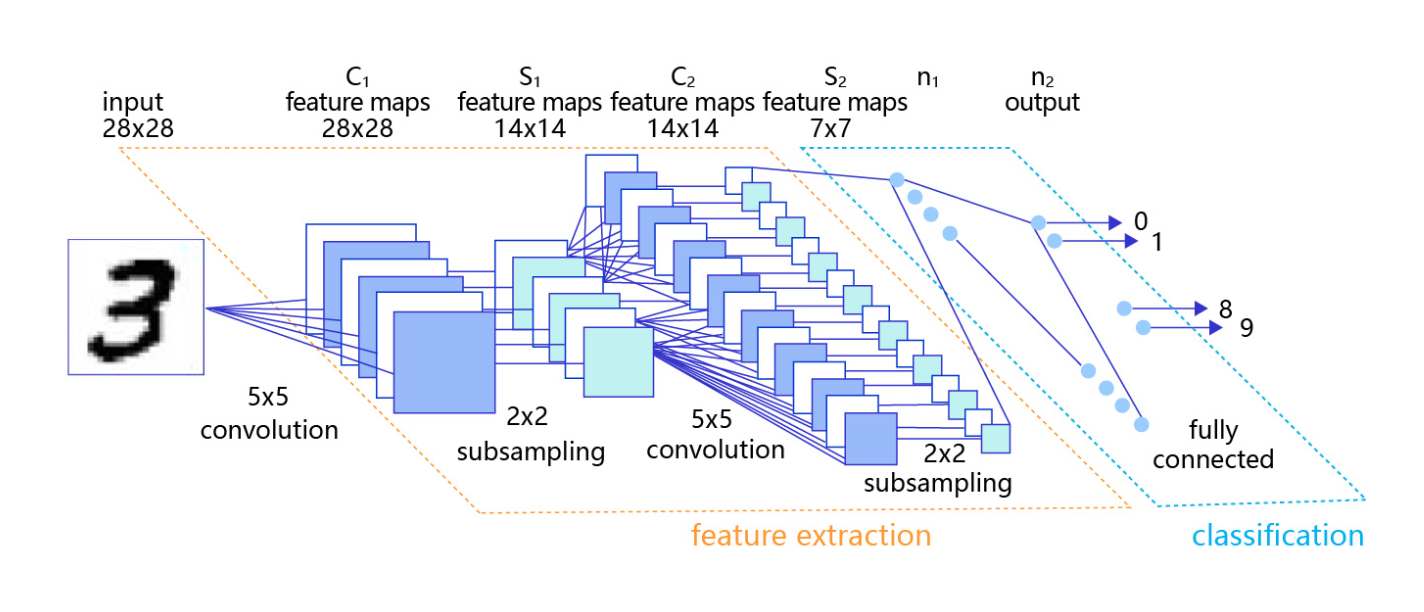
图4:在处理计算机视觉任务中大放异彩的卷积神经网络
卷积层(convolutional layer)、池化层(pooling layer)、步长(stride)、边界填充(pad)
说明:
本节只简单介绍用卷积神经网络实现手写数字识别任务,以及它带来的效果提升。读者可以将卷积神经网络先简单的理解成是一种比经典的全连接神经网络更强大的模型即可,更详细的原理和实现在接下来的第四章-计算机视觉-卷积神经网络基础中讲述。
卷积网络定义
两层卷积和池化的神经网络实现如下所示。
# 多层卷积神经网络实现
class MNIST(fluid.dygraph.Layer):
def __init__(self):
super(MNIST, self).__init__()
# 定义卷积层,输出特征通道num_filters设置为20,卷积核的大小filter_size为5,卷积步长stride=1,padding=2
# 激活函数使用relu
self.conv1 = Conv2D(num_channels=1, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义池化层,池化核pool_size=2,池化步长为2,选择最大池化方式
self.pool1 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义卷积层,输出特征通道num_filters设置为20,卷积核的大小filter_size为5,卷积步长stride=1,padding=2
self.conv2 = Conv2D(num_channels=20, num_filters=20, filter_size=5, stride=1, padding=2, act='relu')
# 定义池化层,池化核pool_size=2,池化步长为2,选择最大池化方式
self.pool2 = Pool2D(pool_size=2, pool_stride=2, pool_type='max')
# 定义一层全连接层,输出维度是1,不使用激活函数
self.fc = Linear(input_dim=980, output_dim=1, act=None)
# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出
def forward(self, inputs):
x = self.conv1(inputs)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = fluid.layers.reshape(x, [x.shape[0], -1])
x = self.fc(x)
return x
模型训练定义
配置模型训练函数:EPOCH=20,batch=100
训练定义好的卷积网络,代码如下:
#网络结构部分之后的代码,保持不变
with fluid.dygraph.guard():
model = MNIST()
model.train()
#调用加载数据的函数
train_loader = load_data('train')
optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01, parameter_list=model.parameters())
EPOCH_NUM = 20
for epoch_id in range(EPOCH_NUM):
for batch_id, data in enumerate(train_loader()):
#准备数据
image_data, label_data = data
image = fluid.dygraph.to_variable(image_data)
label = fluid.dygraph.to_variable(label_data)
#前向计算的过程
predict = model(image)
#计算损失,取一个批次样本损失的平均值
loss = fluid.layers.square_error_cost(predict, label)
avg_loss = fluid.layers.mean(loss)
#每训练了100批次的数据,打印下当前Loss的情况
if batch_id % 200 == 0:
print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
#后向传播,更新参数的过程
avg_loss.backward()
optimizer.minimize(avg_loss)
model.clear_gradients()
#保存模型参数
fluid.save_dygraph(model.state_dict(), 'mnist')
训练输出节选:
...
...
epoch: 17, batch: 0, loss is: [1.3615658]
epoch: 17, batch: 200, loss is: [1.3933234]
epoch: 17, batch: 400, loss is: [1.0364356]
epoch: 18, batch: 0, loss is: [1.3520143]
epoch: 18, batch: 200, loss is: [1.0927333]
epoch: 18, batch: 400, loss is: [1.2897038]
epoch: 19, batch: 0, loss is: [1.2680488]
epoch: 19, batch: 200, loss is: [1.3827461]
epoch: 19, batch: 400, loss is: [0.90689504]
比较经典全连接神经网络和卷积神经网络的损失变化,可以发现卷积神经网络的损失值下降更快,且最终的损失值更小。
模型测试
利用ACC来分别评估全连接网络与卷积神经网络模型性能。
评估函数代码如下:
# 封装评估模型函数
def eval_model(model_class, model_file, data):
# 计算准确率
def calculate_ACC(pres, labels):
assert pres.shape == labels.shape,'pres.shape:{} != labels.shape:{} is required when calculat ACC'.format(pres.shape, labels.shape)
count = 0
for i in pres.astype('int32') == labels:
if i:
count += 1
acc = count / len(labels)
return acc
# 定义飞浆动态图工作环境
imgs, labels = data
with fluid.dygraph.guard():
model = model_class()
model_dict, _ = fluid.load_dygraph(model_file)
# 加载模型参数
model.load_dict(model_dict)
# 设置模型工作模式,灌入测试数据
model.eval()
results = model(fluid.dygraph.to_variable(imgs))
# print('predict results shape:{}'.format(results.numpy().shape))
model_acc = calculate_ACC(results.numpy(), labels)
# print('Acc of model is:{}%'.format(model_acc*100))
return model_acc
# 开始评估
eval_loader = load_data('eval')
acc_list = []
for id, data in enumerate(eval_loader()):
# print('eval images shape is:{}
eval labels shape is:{}'.format(data[0].shape, data[1].shape))
acc_list.append(eval_model(MNIST, 'mnist', data))
# 计算训练20个epoch后模型的预测准确率
print('Acc of model is:{}%'.format(np.mean(acc_list)*100))
输出:
loading mnist dataset from ./work/mnist.json.gz ......
Acc of model is:36.669999999999995%
从最终结果来看效果也不是很理想,这是由于图像识别属于分类问题,目前网络输出为回归后的一个实数。且训练中使用的均方差损失函数,计算输出含义是:输出与实际标签间的差距,并不适用与分类问题。
因此为了提升准确率,需要选择合适的损失函数。下节内容即为损失函数的优化。