欧拉图
定义:
欧拉回路:图G的一个回路,如果恰通过图G的每一条边,则该回路称为欧拉回路,具有欧拉回路的图称为欧拉图。欧拉图就是从图上的一点出发,经过所有边且只能经过一次,最终回到起点的路径。
欧拉通路:即可以不回到起点,但是必须经过每一条边,且只能一次。也叫"一笔画"问题。
性质:
欧拉回路:一个欧拉回路,删掉一个点,仍然是一个欧拉回路。从一个欧拉回路拖走一个小欧拉回路,结果也是一个欧拉回路。
判定(充要):
欧拉回路:1: 图G是连通的,不能有孤立点存在。
2: 对于无向图来说度数为奇数的点个数为0;对于有向图来说每个点的入度必须等于出度。
欧拉通路:1: 图G是连通的,无孤立点存在。
2: 对于无向图来说,度数为奇数的的点可以有2个或者0个,并且这两个奇点其中一个为起点另外一个为终点。对于有向图来说,可以存在两个点,其入度不等于出度,其中一个出度比入度大1,为路径的起点;另外一个入度比出度大1,为路径的终点。
求解欧拉通路,常规方法是暴搜。
1 void DFS(int v){//深度优先遍历 2 for(int i=0;i<graph[v].size();++i){//遍历该点能到达的结点 3 int w=graph[v][i]; 4 if(!visit[v][w]){//该边没有被访问过 5 visit[v][w]=visit[w][v]=true;//该边已被访问 6 DFS(w);//递归遍历 7 } 8 } 9 path.push_back(v);//加入欧拉路径中 10 }
注意要等所有的边遍历完再将节点push,否则一旦一条边走错了那答案就错了。这样的话有了’反悔‘得机会。
(以下讨论无向图)
对于欧拉回路而言,内部无奇度顶点,随便走都可以。
对于欧拉通路,找到两个奇度顶点,不妨设为S和E:
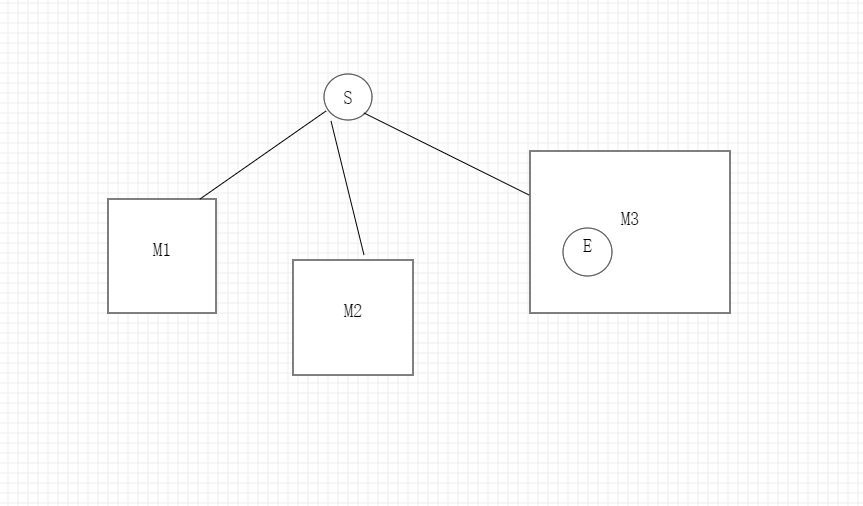
不难发现M1,M2都有欧拉回路,所以S进入到M1/M2时一定可以返回S,但是一旦进入M3就无法回去了,为了避免这种情况,所以要等遍历完所有边再push点,这样可以保证E会是最先push进去的。