区别:
假设检验通常是检验样本对应的总体之间是否有显著性差异
而关联性检验是检验是否显著相关。
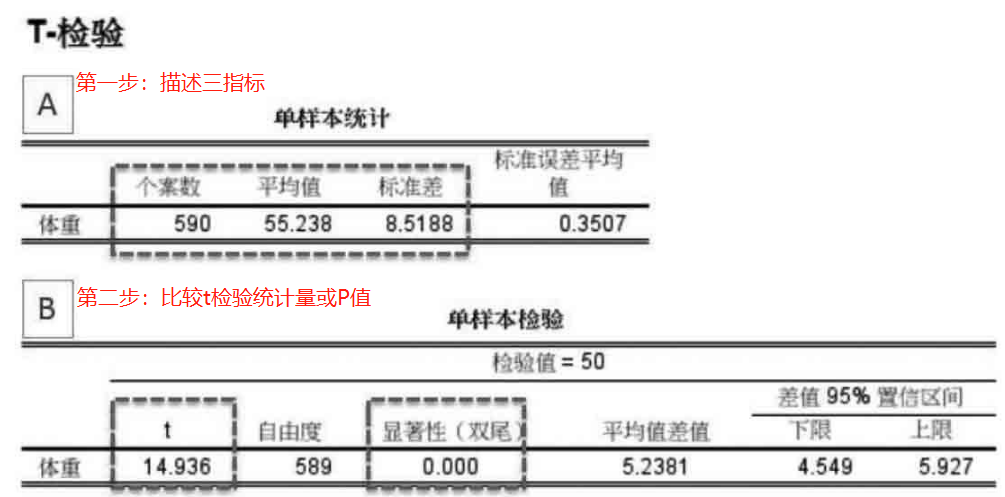
一、单样本t检验
1、设计思想:
两个总体,总体A已知;总体B未知,但其样本已知,问题是未知总体B与已知总体A之间有无差异?实际上是验证该样本是否就是来自这个已知总体A?
2、适用:
(1)已知一个总体和未知总体中的一个样本。
(2)样本数据符合正态分布,不符合时应采用非参检验。

3、SPSS处理解读三步法:
二、配对样本t检验
1、设计思想:
配对样本t检验是配对的两组数据相减变成一组数据,然后去和已知总体0比较,其实就是转化为单样本t检验。
2、适用:
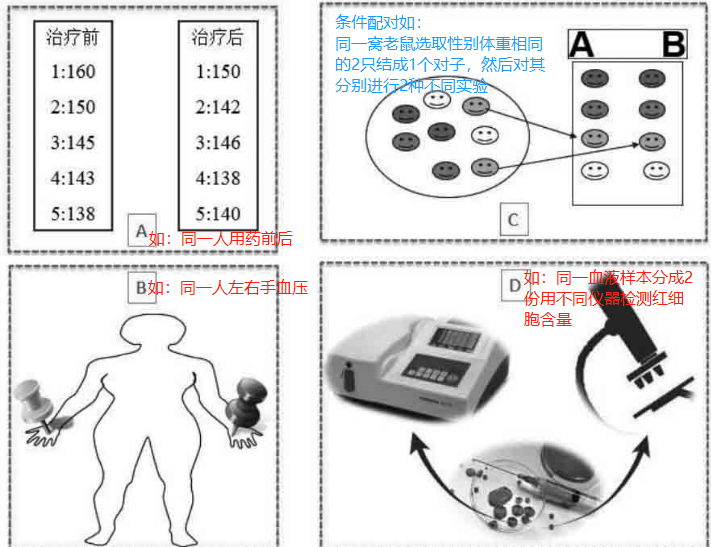
(1)检测的两组配对数据之间存在相关性而不独立,这与两独立样本设计有着本质的区别。包括四种配对类型,3种为同体配对,1种异体配对(条件配对)。
(2)两组样本数据配对差值符合正态分布。
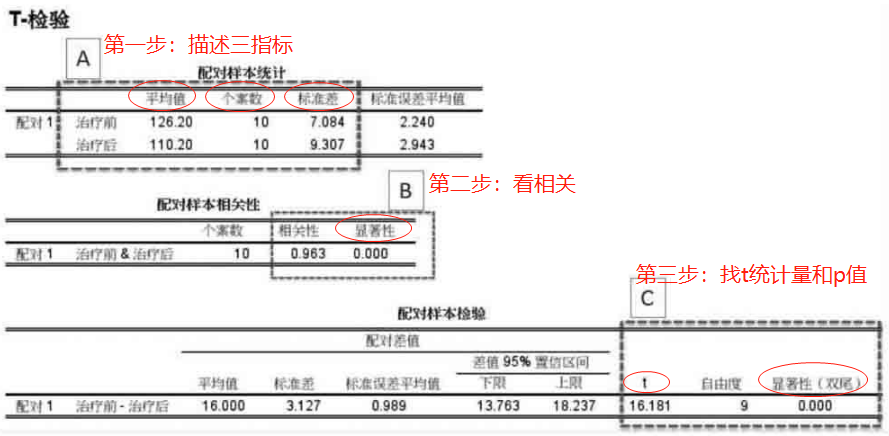
3、SPSS处理解读三步法:
一般,第二步可以忽略。但从统计学角度,这一步是为了验证配对数据的一致性,用于说明实验措施的稳定性。
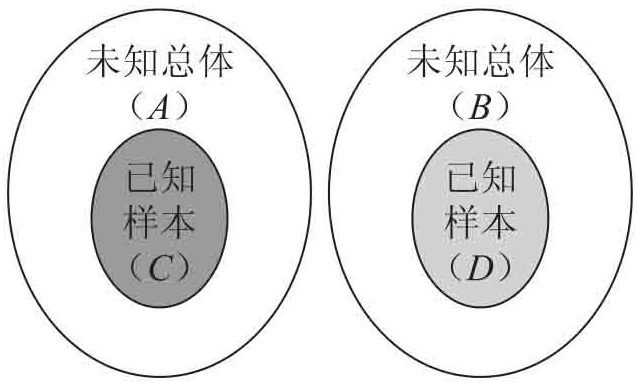
三、两独立样本t检验(A/Btest 背后原理)
1、设计思想:
在两个未知的总体中分别抽取一个样本,然后比较两个总体之间是否有差异?实际是检验两样本所来自总体的均值是否相等。
注意:分为「两总体均值检验」和「两总体率值检验」
2、适用:
(1)独立性。完全随机设计的两样本均值的比较。实践中,两个样本获取只有两种可能:随机分组或按属性分组。不管哪种,均是保证两组相互独立,不受影响。
(2)正态性。两独立样本t检验要求两样本所代表的总体分别服从正态分布N(μ1,σ^2)和N(μ2,σ^2)。
(3)方差齐性。要求两个t分布形态相差不大。即两总体方差σ1^2、σ2^2显著性相等。(ps:若两总体方差不满足齐性,需要先进行变换校正)。
注意:实践中,两个样本的获取只有两种可能:一是随机分组,如60只SD大鼠,随机分2组,每组30只,分别接受不同的处理,然后比较某个计量效应指标;二是按照某种属性特征分组,如某班级按照性别分为男生组和女生组,然后比较男女生某门课程的考试成绩差异。不管是随机分组还是按照属性特征分组,均是保证两组相互独立,不受影响。
两独立样本t检验的检验假设是两总体均值相等,即原假设H0:μ1-μ2=0,统计量计算公式为:
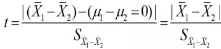
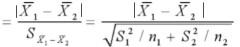
注意:如果是「两总体率值检验」,那么分子是两率值之差,分母 S₁²= p₁(1-p₁),S₂²= p₂(1-p₂)
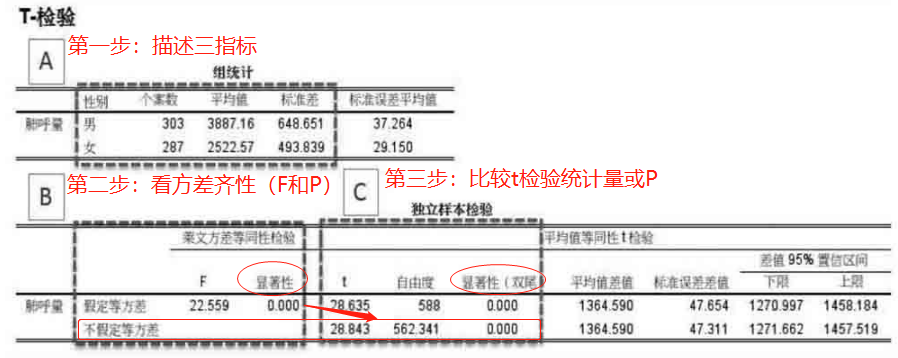
3、SPSS处理解读三步法:
第二步,如果假定等方差 p<0.05,说明两组t分布形态差异过大,不适合比较。那么第三步就应该看不假定等方差对应的t或p值。
4、举例:
25例糖尿病患者随机分成两组,对照组甲单纯药物治疗,实验组乙采用药物合并饮食治疗,二月后测空腹血糖如下,问两种疗法血糖值是否相同?
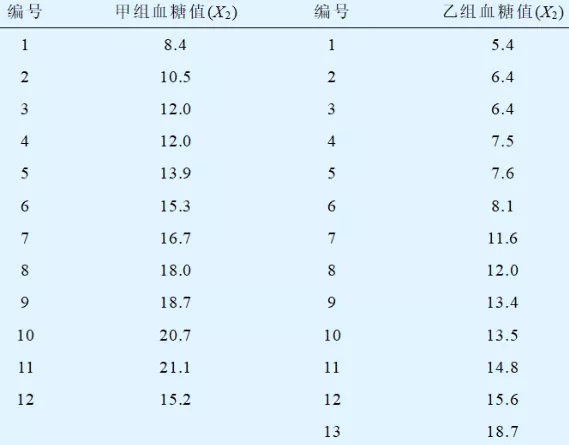
数据情况(描述三指标):
对照组甲 样本量n1=12,样本均值x1=15.2 ,样本标准差s1=182.5
实验组乙 n2=13,x2=9.8,s2=141
检验步骤:
1)对样本总体关系提出假设,选择合适的检验方法,设定检验水平(给定显著性水平或临界值)
原假设H0:u1 =u2
备择假设H1:u1≠u2
设定显著性水平α=0.05,因备择假设是H1:u1≠u2,故采用双边检验;
因是两组独立样本均值的差异性检验,且两总体标准差未知,且故选用 t检验方法。
2)根据样本计算检验统计量值(t检验统计量或p值)
代入公式计算得 t=2.639
3)比较检验统计量值与检验水平大小,做出推断结论。
因为是α=0.05且双侧检验,自由度 v =n1+n2-2=23 ,查t 临界值表可知 tα/2=2.069;
所以t=2.639 >tα/2=2.069(也可以通过比较算得的p值是否小于α,判断),落在拒绝域,则拒绝原假设H0,接受备择假设H1。故认为两种疗法效果不同。