62、不同路径
基本思想:
动态规划
具体实现:
1.确定dp数组以及下标的含义
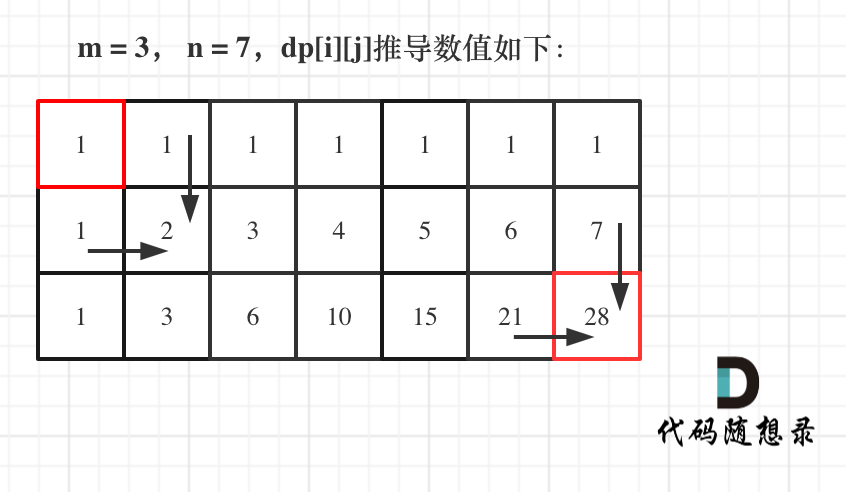
dp[i][j]:表示从(0,0)出发,到(i,j)有dp[i][j]条不同的路径
2.确定递推公式
求dp[i][j],两个方向来推导,即dp[i - 1][j] 和 dp[i][j - 1]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
3.dp数组的初始化
dp[i][0]都是1:从(0,0)到(i,0)的路劲只有一条
dp[0][j]同理
4.确定遍历顺序
从上方和左方推导来
5.举例推导
代码:
class Solution { public int uniquePaths(int m, int n) { int[][] dp = new int[m][n]; for (int i = 0; i < m; i++) { dp[i][0] = 1; } for (int j = 0; j < n; j++){ dp[0][j] = 1; } for (int i = 1; i < m; i++){ for (int j = 1; j < n; j++){ dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[m - 1][n - 1]; } }
优化:
class Solution { public int uniquePaths(int m, int n) { int[] dp = new int[n]; for (int j = 0; j < n; j++){ dp[j] = 1; } for (int i = 1; i < m; i++){ for (int j = 1; j < n; j++){ dp[j] += dp[j - 1]; } } return dp[n - 1]; } }
63、不同路径ii
基本思想:
在上题的基础上,如果碰到障碍物时,dp数组保持为初始状态
具体实现:
1、确定dp数组以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
2、确定递推公式
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
(i,j)如果是障碍的话,保持初始状态
3.dp数组初始化
先把dp数组都初始化为0,(不过dp数组刚创建的时候就是0)
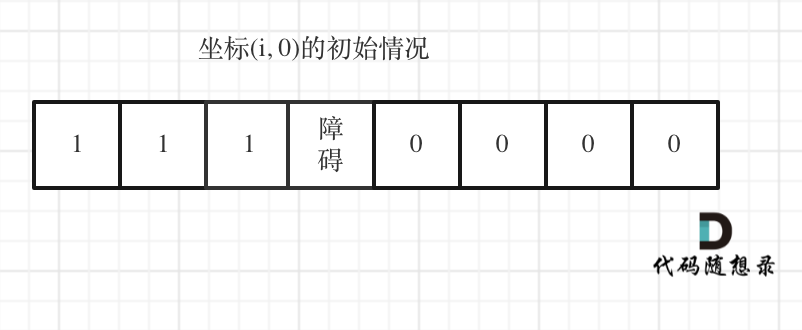
dp[i][0]是1:从(0,0)到(i,0)的路劲只有一条
dp[0][j]同理
但是如果(i,0)这条边有障碍之后,障碍和障碍之后都是走不到的位置,障碍之后的dp[i][0]是0
4.确定遍历顺序
从上方和左方推导
从上到下,从左到右
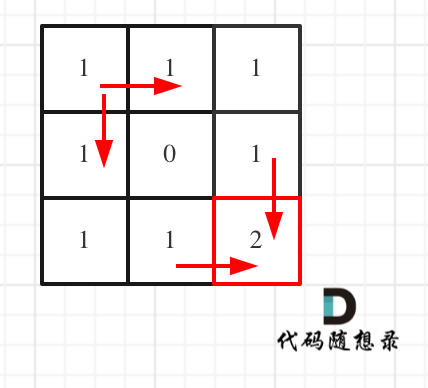
5.举例
obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
代码:
class Solution { public int uniquePathsWithObstacles(int[][] obstacleGrid) { int m = obstacleGrid.length; int n = obstacleGrid[0].length; int[][] dp = new int[m][n]; dp[0][0] = 1 - obstacleGrid[0][0]; for (int i = 1; i < m; i++) { if (obstacleGrid[i][0] == 0 && dp[i-1][0] == 1) dp[i][0] = 1; } for (int i = 1; i < n; i++) { if (obstacleGrid[0][i] == 0 && dp[0][i-1] == 1) dp[0][i] = 1; } for (int i = 1; i < m; i++){ for (int j = 1; j < n; j++){ if (obstacleGrid[i][j] == 1) continue; dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[m - 1][n - 1]; } }