516、最长回文子序列
基本思想:
动态规划运用二维dp数组
具体实现:
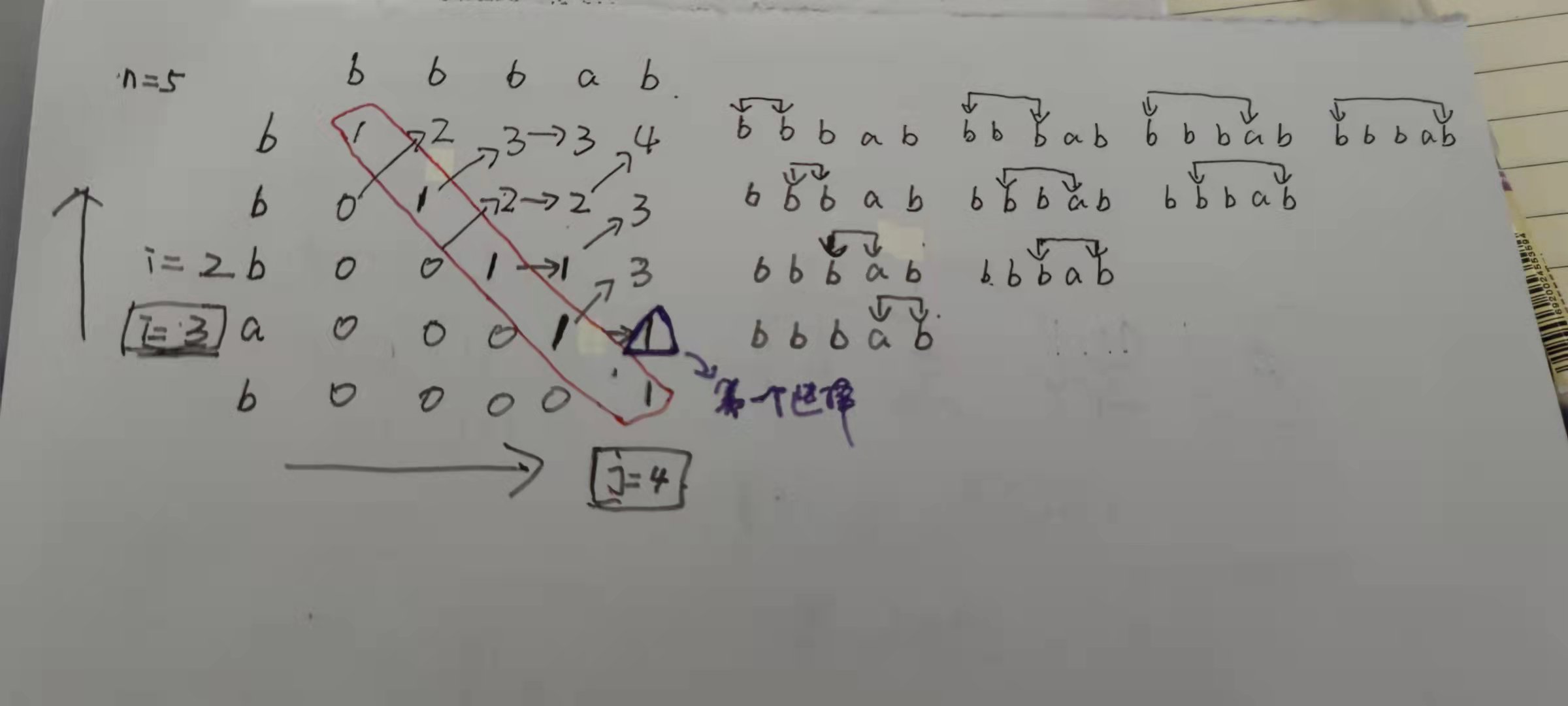
1、确定状态:
(1)最后一步----字符串s[i:j]中的最长回文子序列的长度
(2)子问题

2、转移方程
(1)s[i]==s[j]
把字符串左右同时缩小一下+2,上图情况1 +2
(2)s[i]!=s[j]
不相等的话说明这两个字符不可能同时出现在s[i:j]的最长回文子序列
选择上图情况2和3较大的一个
3、初始状态
dp[i][i] = 1
i比j大的地方dp都是0
因为i永远在j的前面
4、计算顺序
从左到右 知道j,要先知道 j-1
从下到上 知道i,要先知道 i+1

代码:
class Solution: def longestPalindromeSubseq(self, s: str) -> int: n = len(s) dp=[[0]*n for i in range(n)] for i in range(n): dp[i][i] = 1 for i in range(n-2,-1,-1): for j in range(i+1,n): if s[i] == s[j]: dp[i][j] = dp[i+1][j-1] +2 else: dp[i][j] = max(dp[i+1][j],dp[i][j-1]) return dp[0][n-1]
72、编辑距离
基本思想:
动态规划,二维数组
具体实现:
1、确定状态:
(1)最后一步--dp[i][j]表示s1[0.....i-1]和s2[0......j-1]的编辑距离
(2)子问题

i索引对应的是需要改变的
插入--在i的后面插入j对应的字符,插入完以后j往前一步, i不动
删除--删除i对应的字符,删除完以后i往前一步,j不动
替换--把i对应的字符替换成j对应的字符,替换完都往前走一步
跳过--说明i和j对应的字符相同,dp[i][j] == dp[i-1][j-1]
2、状态转移方程:
(1)word1[i] == word[j]
dp[i][j] == dp[i-1][j-1]
(2)word1[i] != word[j]
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
3、初始状态:
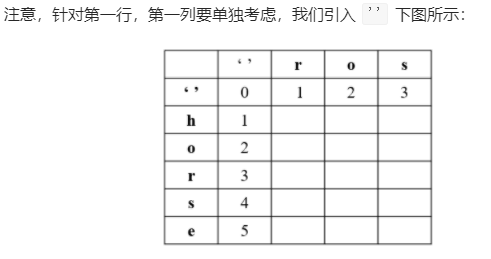
horse是word1,ros是word2
第一行,word1为空,word1变成word2的最少步数就是插入操作
第一列,Word2为空,word1变成word2的最少步数就是删除操作
4、计算顺序:
从左到右,从上到下
代码:
class Solution: def minDistance(self, word1: str, word2: str) -> int: m = len(word1) n = len(word2) dp = [[0 for _ in range(n+1)]for _ in range(m+1)] for i in range(1,m+1): dp[i][0] = i for j in range(1,n+1): dp[0][j] = j for i in range(1,m+1): for j in range(1,n+1): if word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1] else: dp[i][j] = 1+min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1]) return dp[m][n]
1312、以最小插入次数构造回文串
基本思想:
动态规划
具体实现:
1、确定状态:
最后一步---dp[i][j]表示构成的回文串的插入最少的次数
子问题---dp[i][j-1],dp[i+1][j],dp[i+1][j-1]构成回文串的插入最少的次数
2、状态转移方程:
(1)s[i] == s[j]
不需要任何插入,只要看s[i+1....j-1]是否是回文串就行了
dp[i][j] = dp[i+1][j-1]
(2)s[i] != s[j]
dp[i+1][j] ,dp[i][j-1] 其中次数少的一种至少插入一个字符
3、初始状态:
i == j时,dp[i][j]=0
4、计算顺序
从左到右,从下到上
代码:
class Solution: def minInsertions(self, s: str) -> int: n = len(s) dp = [[0]*n for _ in range(n)] for i in range(n-2,-1,-1): for j in range(i+1,n): if s[i] == s[j]: dp[i][j] = dp[i+1][j-1] else: dp[i][j] = 1 + min(dp[i+1][j], dp[i][j-1]) return dp[0][n-1]
空间复杂度降低
class Solution: def minInsertions(self, s: str) -> int: n = len(s) dp = [0]*n for i in range(n-2,-1,-1): pre = 0 for j in range(i+1,n): temp = dp[j] if s[i] == s[j]: dp[j] = pre else: dp[j] = 1 + min(dp[j], dp[j-1]) pre = temp return dp[n-1]