2019暑假(大二结束大三开始):
线性代数学习、《精通数据科学》阅读、DE算法的学习与改进及论文写作、数据结构的C语言实现、数学建模相关准备、多文件编程
本篇是一些零星琐碎的笔记
DE有关的论文阅读笔记记在OneNote上了
DE差分进化算法Differential Evolution作者网站:http://www1.icsi.berkeley.edu/~storn/code.html#hist
(kao为什么我看不懂别人写的代码菜鸡落泪气死自己了)
(没带C++课本回家现在好难过 忘记好多)//运算符重载https://www.runoob.com/cplusplus/cpp-overloading.html
C++风格的强制类型转换:static_cast<double>(x)
->和.的区别?
->主要用于类类型的指针访问类的成员,而.运算符,主要用于类类型的对象访问类的成员
鲁棒性:鲁棒性和稳定性都是反应控制系统抗干扰能力的参数。
鲁棒性,是指控制系统在一定(结构,大小)的参数摄动下,维持其它某些性能的特性。
稳定性,是指控制系统在使它偏离平衡状态的扰动作用消失后,返回原来平衡状态的能力。
安装pyecharts
阅读《精通数据科学:从线性回归到深度学习》的一些琐碎的笔记

chapter1概述
keys: 特征提取 矩阵运算 分布式机器学习 模型预测效果 模型参数稳定性 模型结果的可解释性
对数据搭建模型:数据模型(data model)---传统统计模型、 算法模型(algorithm model)--机器学习

chapter2Python
魔术命令:https://ipython.readthedocs.io/en/stable/interactive/magics.html
def wordCount(data): """ 统计列表中字符串出现的次数 参数 ---- data:list[str],需要统计的字符串列表 返回 --- re:dict,结果hash表 """ re={} for i in data: re[i] = re.get(i,0)+1 return re if __name__ == "__main__": data=["ab","cd","ab","d","d"] print ("The results is %s" % wordCount(data))
The results is {'ab': 2, 'cd': 1, 'd': 2}
__name__和__doc__都是内置属性
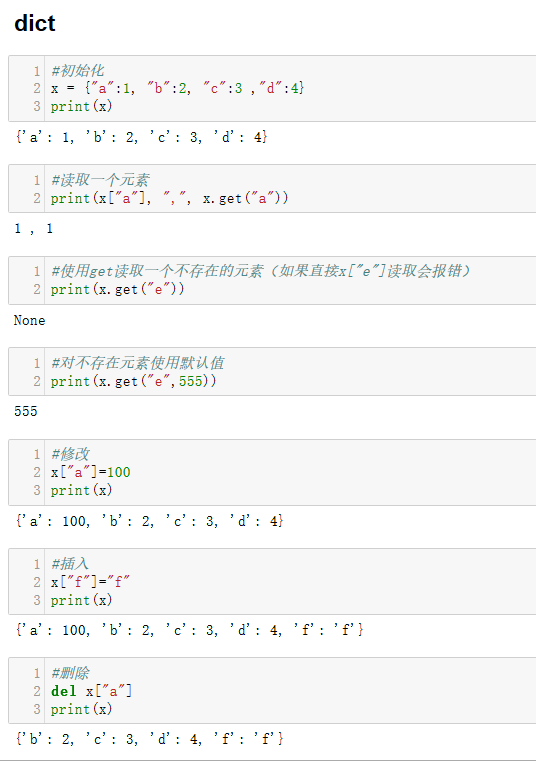
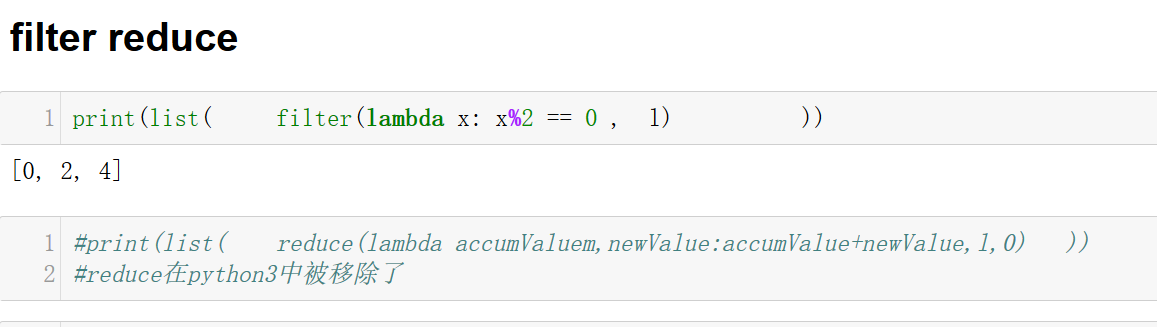
基本数据类型:dict list tuple 表达式:lambda 内置函数:map reduce filter



运行map()后,报:<map object at 0x02629E50>解决方法:
因为在python3里面,map()的返回值已经不再是list,而是iterators, 所以想要使用,只用将iterator 转换成list 即可, 比如 list(map())



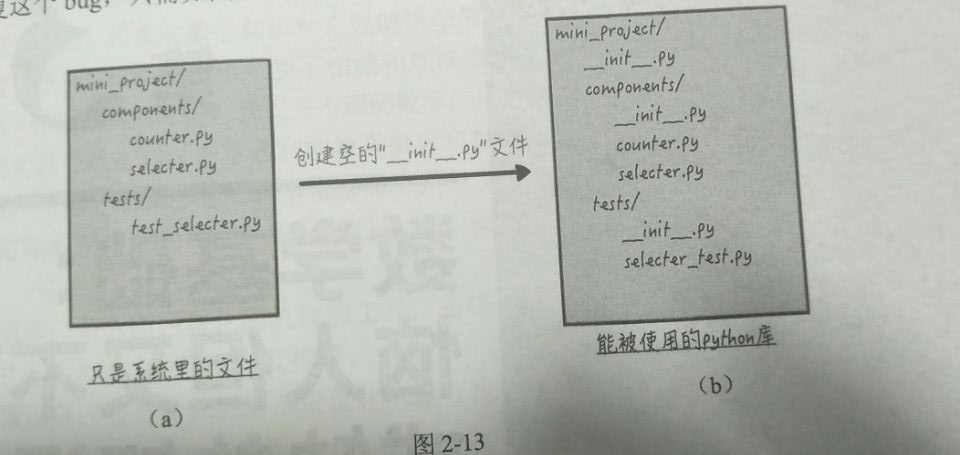
Python的工程结构
Python库实际上是一个包含__init__.py(空)文件的目录
chapter3数学
Young man, in mathematics you don't understand things. You just get used to them.
矩阵、概率、微积分
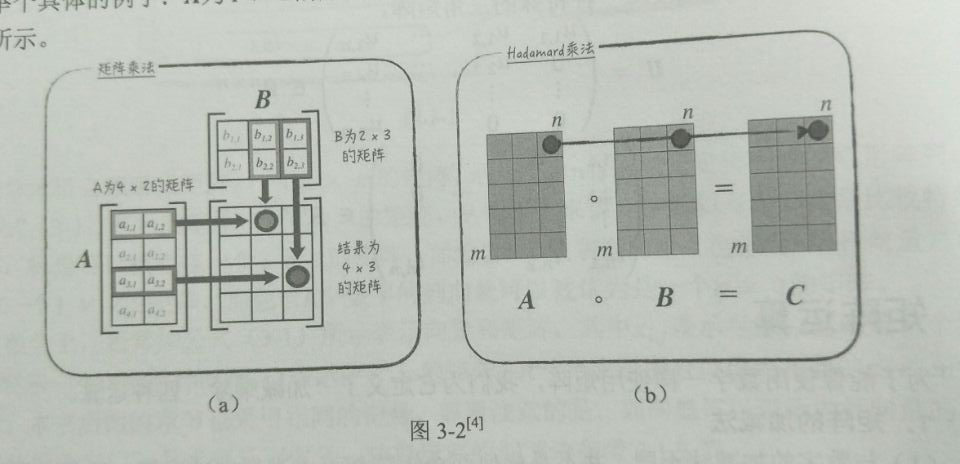
Python中两种表示矩阵的方法:matrix类、array类
matrix类--默认乘法为矩阵乘法
array类--默认乘法为Hadamard乘法(numpy的各种实现?)
chapter4线性回归
机器学习角度:
1.确定场景类型——监督、非监督?回归、分类、聚类、降维?
2.定义损失函数——目标:使损失函数最小
3.提取特征——清洗数据、特征
4.确定模型形式、估计参数——
5.评估模型效果——线性模型的均方差?决定系数?
统计学角度:
1.假设条件概率——参数?噪声服从正态分布
2.估计参数——似然函数、最大似然估计法等
3.推导参数分布
4.假设检验与置信区间
陷阱:过度拟合和模型幻觉
过度拟合:
交叉验证:划分测试集和训练集。
训练误差和测试误差
模型幻觉:
假设检验、置信区间(统计学)
惩罚项(正则化)、超参数
如果模型含超参数,交叉验证划分为训练集(train set)和测试集(test set),如果不含超参数,则划为训练集(train set)、验证集(validation set)、测试集(test set)
模型持久化
python——python: pickle(import pickle;pickle.dump(model,open(modelPath,"wb"); model=pickle.load( open(modelPath,"rb") ) )
任何语言——任何语言: PPML(利用XML描述),有比较成熟的工具可以使用
chapter5 逻辑回归
To be, or not to be, that is a question.
逻辑分布,。。。。。。。
数值型变量和类别型变量
describe方法:
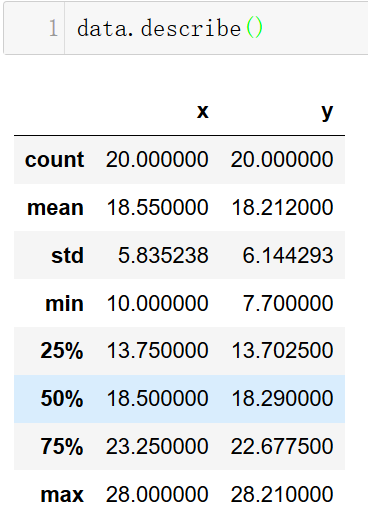
交叉报表
划分训练集和测试集:使用skitlearn中的train_test_split函数。