1009 Tree and Permutation
题解:可以这样考虑,1和2绑定在一起的排列(因为(1,2)和(2,1)是不同的,所以要乘2)有2 * (n - 1) * fac[ n - 2]种,所以ans = 2 * (n - 1) * fac[n - 2] * ∑i=1∑j=i+1d(i, j)。而后面那部分的计算方式比较常见,就是考虑每条边在哪些点对中出现过。
ps:fac[ i ]表示 i 的阶乘,d(i, j)表示点 i 到点 j 的距离。

const int N = 100005; const int mod = 1000000007; int n, tot; int head[N], d[N], fac[N]; LL sum; struct node { int to, next, va; }e[N * 2]; void Inite() { tot = sum = 0; mem(head, -1), mem(d, 0); } void addedge(int u, int v, int w) { e[tot].to = v, e[tot].va = w, e[tot].next = head[u], head[u] = tot++; } void DFS(int u, int p) { d[u] = 1; for (int i = head[u]; ~i; i = e[i].next) if (e[i].to != p) { int v = e[i].to; DFS(v, u); d[u] += d[v]; } } void DFS2(int u, int p) { for (int i = head[u]; ~i; i = e[i].next) if (e[i].to != p) { int v = e[i].to; sum += 1ll * d[v] * (n - d[v]) % mod * e[i].va % mod; sum %= mod; DFS2(v, u); } } void Solve() { DFS(1, 0); DFS2(1, 0); LL ans = 1ll * 2 * (n - 1) * fac[n - 2] % mod * sum % mod; printf("%lld ", ans); } int main() { fac[0] = 1; rep(i, 1, N) fac[i] = 1ll * fac[i - 1] * i % mod; while(sc(n) != EOF) { Inite(); Rep(i, 2, n) { int u, v, w; sc(u), sc(v), sc(w); addedge(u, v, w); addedge(v, u, w); } Solve(); } return 0; }
1010 YJJ's Salesman
题解:将点按x升序y降序的顺序排序。然后对列建一个线段树,维护区间最大值。这有什么用呢?
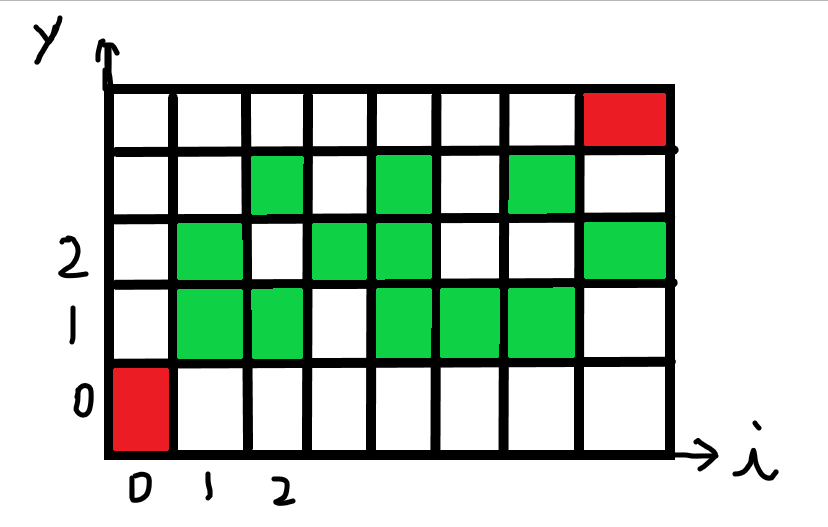
dp[ i ][ j ]:表示走到(i,j)这个位置得到的最大money,那么 dp[ i ][ j ] 一定是 dp [ i - 1 ][ 0 ~ ( j - 1) ]某个位置转移过来的,且这个位置就是 (0, ( j - 1)) 这个区间的最大值。

const int N = 100005; int n; int Max[4 * N]; unordered_map<int, int> H; struct node { int x, y, va; } p[N]; bool cmp(node a, node b) { if (a.x == b.x) return a.y > b.y; return a.x < b.x; } inline bool cmpY(node a, node b) { return a.y < b.y; } inline void upd(int &x, int y) { (x < y) && (x = y); } void Pushup(int root) { Max[root] = max(Max[lson], Max[rson]); } void Update(int l, int r, int root, int pos, int x) { if (l == r) { Max[root] = x; return; } int mid = (l + r) >> 1; if (pos <= mid) Update(l ,mid, lson, pos, x); else Update(mid + 1, r, rson, pos, x); Pushup(root); } int Query(int l, int r, int root, int L, int R) { if (l > R || r < L || L > R) return 0; if (L <= l && r <= R) return Max[root]; int mid = (l + r) >> 1; int ans = 0; upd(ans, Query(l, mid, lson, L, R)); upd(ans, Query(mid + 1,r, rson, L, R)); return ans; } int main() { BEGIN() { mem(Max, 0); H.clear(); sc(n); Rep(i, 1, n) sc(p[i].x), sc(p[i].y), sc(p[i].va); int cnt = 0; sort(p + 1, p + n + 1, cmpY); Rep(i, 1, n) if (p[i].y != p[i - 1].y) H[p[i].y] = ++cnt; sort(p + 1, p + n + 1, cmp); Rep(i, 1, n) { int tp = Query(1, cnt, 1, 1, H[p[i].y] - 1) + p[i].va; int sp = Query(1, cnt, 1, H[p[i].y], H[p[i].y]); if (tp > sp) Update(1, cnt, 1, H[p[i].y], tp); } pr(Max[1]); } return 0; }
