Valid Sets CodeForces

As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value a_i associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:

1. S is non-empty.
2. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S.
3. .

Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007 (10⁹ + 7).

Input

The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).

The second line contains n space-separated positive integers a₁, a₂, ..., a_n(1 ≤ a_i ≤ 2000).

Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output

Print the number of valid sets modulo 1000000007.

Example

Input

1 4
2 1 3 2
1 2
1 3
3 4

Output

8

Input

0 3
1 2 3
1 2
2 3

Output

3

Input

4 8
7 8 7 5 4 6 4 10
1 6
1 2
5 8
1 3
3 5
6 7
3 4

Output

41

Note

In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set {1, 2, 3, 4} is not valid, because the third condition isn't satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.

题意：求一棵树中满足特殊条件的连通子图的个数（该连通子图中节点最大值与最小值之差不超过d）

题解： Firstly, we solve the case d =  + ∞. In this case, we can forget all a_i since they doesn't play a role anymore. Consider the tree is rooted at node 1.  Let F_i be the number of valid sets contain node i and several other nodes in subtree of i ("several" here means 0 or more). We can easily calculate F_i through F_j where j is directed child node of i: 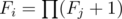. Complexity: O(n).

General case: d ≥ 0. For each node i, we count the number of valid sets contain node i and some other node j such that a_i ≤ a_j ≤ a_i + d (that means, node i have the smallest value a in the set). How? Start DFS from node i, visit only nodes j such that a_i ≤ a_j ≤ a_i + d. Then all nodes have visited form another tree. Just apply case d =  + ∞ for this new tree. We have to count n times, each time take O(n), so the overall complexity is O(n²). (Be craeful with duplicate counting)

意思是说，枚举最大值点（哇，又一次被打击了，满脑子骚操作，以为是DFS序，然后转区间巴拉巴拉的，结果直接枚举，orzzzzz）

并以该点为根跑一遍DFS，算满足条件的子树个数。区间重复问题：两个点a,b的值相同，当以a为根时，把b包含了，那么可能以b为

根时把a包含了，这样就可能重复一个区间，注意是可能。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

const int mod=1e9+7;

int d,n;
int a[2005],dp[2005];
bool vis[2005];

vector<int> G[2005];

void DFS(int u,int root){
    dp[u]=1;
    vis[u]=true;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(vis[v]) continue;
        if(a[v]==a[root]&&v<root) continue;          //为了避免区间重复，规定方向，只能从小的编号走向大的。出题人就是强
        if(a[v]<a[root]||a[v]>a[root]+d) continue;
        
        DFS(v,root);
        dp[u]=((ll)dp[u]*(dp[v]+1))%mod;
    }
}

int main()
{   cin>>d>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=2;i<=n;i++){
        int p,q;
        cin>>p>>q;
        G[p].push_back(q);
        G[q].push_back(p); 
    }
    int ans=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){ dp[j]=0; vis[j]=false; }
        DFS(i,i);
        ans=(ans+dp[i])%mod; 
    }
    cout<<ans<<endl;
}