一、函数极限的概念
函数极限的引入
数列{xn}:xn = f(n)
lim n->∞ xn=a : 当自变量n取正数而无限增大时,f(n)无限接近于确定的数a
函数的极限:在自变量的某个变化过程中,如果对应的函数值无限接近于某个确定的数,那么这个确定的数就叫做在一变化古城中的函数的极限
自变量变化的两种情况:
1.自变量x任意地接近于有限值x0(记作x->x0) 对应地函数值f(x)地变化情形
2.自变量x地绝对值|x|无限增大(记作x->∞) 对应地函数值f(x)的变化情形
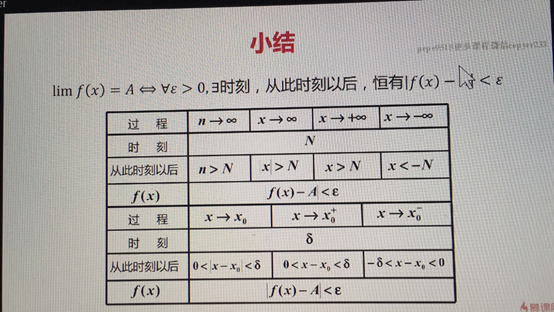
自变量变化的过程:x->x0 f(x)->A 称A是f(x)当x->x0时的极限
f(x)无限接近于A
|f(x)-A|可以任意小
|f(x)-A|>
x无限接近于0
x->x0
0<|x-x0|<
是某个正数 是以 为半径 x0点的去心邻域
自变量趋于有限值时函数的极限
如果对于任意给定的正数 (不论他多么小
·总存在正数 使得对于适合不等式0<|x-x0|< 的一切x,
·所对应的函数值f(x)都满足不等式|f(x)-A|<
·那么常数A就叫做函数f(x)当x->x0时的极限
记作 f(x) = A 或f(x)->A(当x->x0)

注意
·注1:函数极限与f(x)在x0是否有定义无关
·注2: 与任意给定的正数
·注3:找到一个 ,它体现了x接近x0的程度
二、函数极限例题与单侧极限


单侧极限

定理: 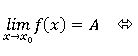
ó f(x0+0) = f(x0-0) =A

左右极限存在但是不相等 函数极限不存在
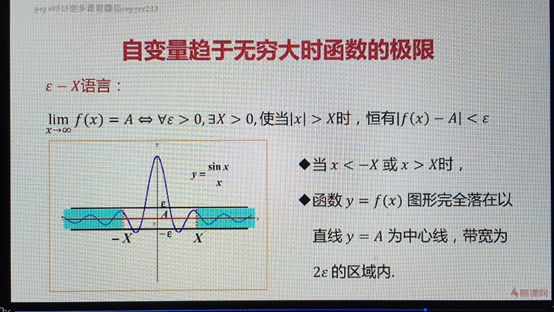
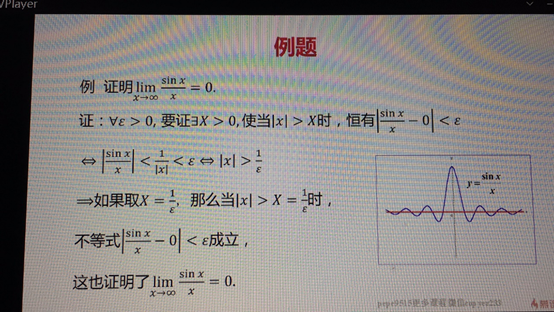
自变量趋于无穷大时函数的极限
·如果对于任意给定的正数 (不论他多么小)
·总存在着正数X 使得对于适合不等式|x|>X的一切x
·所对应的函数值f(x)都满足不等式|f(x)-A|<
·那么常熟A就叫做f(x)当x->∞的极限
记作 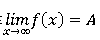
或f(x)->A(当x->∞)

三、函数极限 的性质
1.唯一性
定理:如果limx->x0f(x)存在 那么此极限唯一
2.局部有界性
如果limx-x0 f(x) = A那么存在常熟M>0和δ>0 使得当
0<|x-x0|<δ时,有|f(x)|<=M
3.局部保号性
定理:如果lim x->x0 f(x) = A 且A>0(或A<0) 那么存在常数δ>0 使得当0<|x-x0|<δ时 有f(x)>0(或f(x)<0)
4.函数极限与数列极限的关系
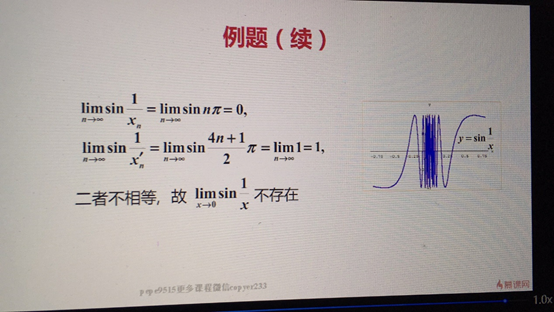
定理:如果limx->x0 f(x)存在,{xn}为函数f(x)的定义域内任一收敛于x0的数列 且满足xn≠x0 那么响应的函数值数列{f(xn)}必收敛,且limn->∞f(xn) = lim x->x0 f(x)
2.局部有界性
如果limx-x0 f(x) = A那么存在常熟M>0和δ>0 使得当
0<|x-x0|<δ时,有|f(x)|<=M
3.局部保号性
定理:如果lim x->x0 f(x) = A 且A>0(或A<0) 那么存在常数δ>0 使得当0<|x-x0|<δ时 有

四、小结