微分中值定理(一系列定理总称)-罗尔定理
费马引理->罗尔定理->拉格朗日中值定理->柯西中值定理


导数为0的点称为驻点



连续、可导、在端点函数值相等。
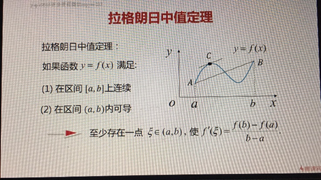
2.微分中值定理——拉格朗日中值定理



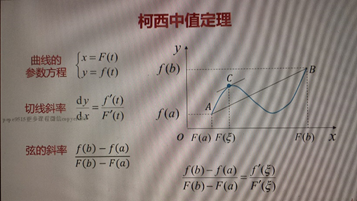
微分中值定理——柯西中值定理




总结一下:
费马引理:
函数f(x)在点ξ的某邻域U(ξ)内有定义,并且在ξ处可导,如果对于任意的x∈U(ξ),都有f(x)≤f(ξ) (或f(x)≥f(ξ) ),那么f '(ξ)=0。

罗尔定理:
如果 R 上的函数 f(x) 满足以下条件:(1)在闭区间 [a,b] 上连续,(2)在开区间 (a,b) 内可导,(3)f(a)=f(b),则至少存在一个 ξ∈(a,b),使得 f'(ξ)=0。:
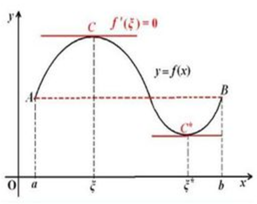
拉格朗日中值定理:
如果函数f(x)满足:
那么在开区间(a,b)内至少有一点

使等式

成立。



拉格朗日中值定理特别像微分近似公式,所以拉格朗日中值定理也叫微分中值定理。
10-4 洛必达法则 00型未定式





注意:在满足定理条件下有些时候洛必达法则也不能解决问题
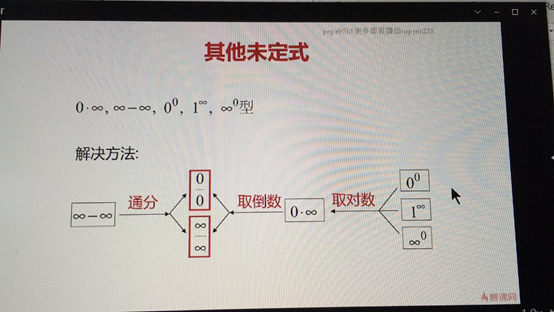
洛必达法则——其他未定式
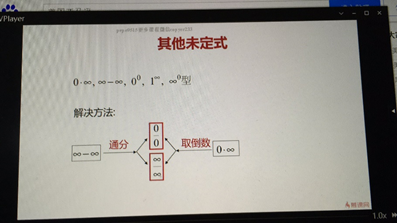


10-6 泰勒公式 泰勒中值定理







10-7 麦克劳林公式










10-8 函数的单调性


9 函数的凹凸性


拐点:凹凸性改变的点叫拐点



小结

10 函数极值的概念


注意
注1:函数的极值是函数的局部性质
注2:对常见函数,极值可能出现在导数为0或不存在的点





11 函数极值求法


如果二阶导数为0的时候,就不能用这个了还是用第一充分条件
12 函数的最大值和最小值


2.连续函数的最值
13 函数图形的描绘




一阶导数为0 驻点
二阶导数为0 拐点的必要条件

小结
1.曲线渐近线球阀
水平渐近线和垂直渐近线
2.函数图形的描绘方法