一、函数的连续性
增量
变量u:初值u1 -> 终值u2
增量Δu: Δu = u2-u1
正的增量Δu:u1变到u2时是增大的
负的增量Δu:u1变到u2时是减小的
函数的增量
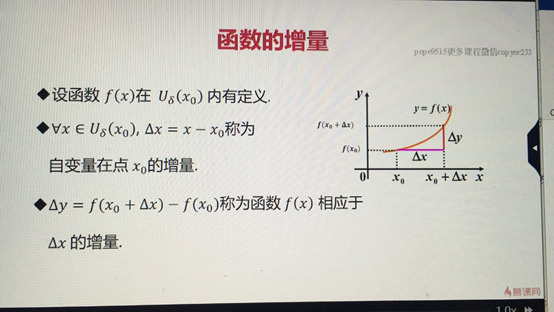

即:当因变量增量随自变量增量趋于0,称为连续。



单侧连续
·左连续:如果limx->x0- f(x)存在且等于f(x0) 即f(x0-) = f(x0)
·右连续:如果limx->x0+f(x)存在且等于f(x0) 即f(x0+) = f(x0)
·定理 函数f(x)在x0处连续=函数f(x)在x0处既左连续又右连续
连续函数
定义:在区间上每一点都连续的函数,叫做在该区间上的连续函数
或者说函数在该区间上连续
注1 如果区间包括端点,那么函数在右端点处左连续,在左端点处右连续
注2 连续函数的图形是一条连续而不间断的曲线
例题
例 证明函数y = sinx 在区间(-∞,+∞)内连续

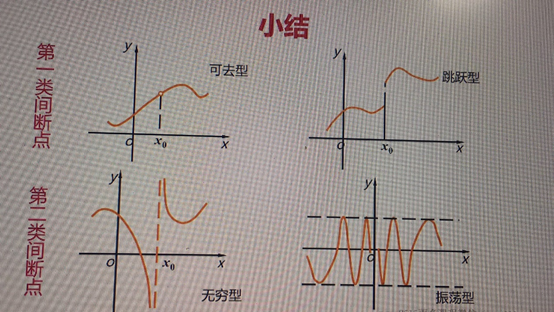
二、函数的间断点
第一类间断点(左右极限都存在)

跳跃间断点
·如果f(x)在x0处左右极限都存在
·但f(x0-0)≠f(x0+0)
则称点x0为函数f(x)的跳跃间断点
讨论f(x) = { -x,x<=0 1+x,x>0} 在x=0处的连续性

可去间断点
·如果f(x)在x0处极限存在
·但limx->x0 f(x) = A ≠f(x0) 或在点x0处无定义
则称点x0为函数f(x)的可去间断点

注意
·注1:可去间断点只要改变或者补充间断处函数的定义,则可使其变为连续点
·注2:跳跃间断点与可去间断点统称为第一类间断点
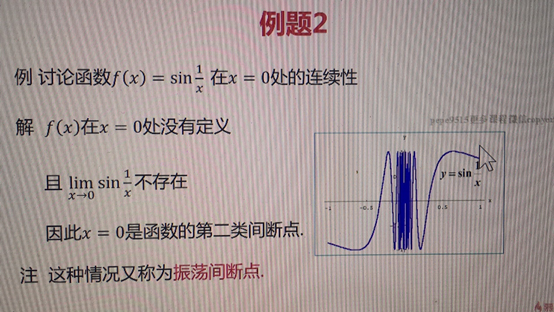
第二类间断点
·如果f(x)在x0处左右极限至少有一个不存在
·则称x0为函数f(x)的第二类间断点
例题1
讨论f(x) = { 1/x (x>0 x(x<=0 ) 在x=0处的连续性


四、章小结
·函数在一点连续必须满足的三个条件;
1.在这一点有定义
2.在这一点极限是存在的
3.极限存在的情况下 还要等于在这一点的函数值
·区间上的连续函数;
函数在区间上的任意一点都连续,我们就说函数在区间上是连续的
·间断点的分类与判别;
间断点{
第一类间断点:可去型,跳跃型 (左右极限都存在
第二类间断点:无穷型, 振荡型 (至少有一个极限不存在
}