今天讲了并查集、堆和Hash表,并讲了几道比较难的题.
例1.
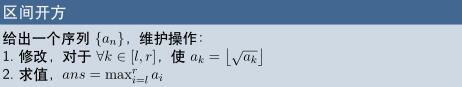
分析:其实这道题我们用一颗很普通的线段树,维护区间最大值就好了,因为最大值开方后还是最大值嘛.
但是开方有一个比较重要的性质:一个10^7的数大概7,8次开方就是1了,以后不管怎么开方都是1,我们能不能不考虑这部分1呢?也就是说,我们能不能用一个数据结构跳过1呢?可以想到用双向链表,但是这样能不能做到线性呢?回想一下链表的操作,我们的第一步是要“找到”链表,也就是说我们要找到当前区间的第一个不是1的表头,这样其实很容易卡掉,考虑一组数据:21111112,如果我们当前处理的区间是[2,6],那么我们要寻找整个区间,复杂度O(nq),通不过所有测试点,能不能有一个数据结构,当我们处理到某个点时,能够跳到下一个非1的点呢?我们考虑这样做: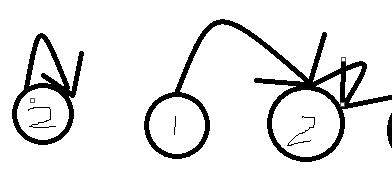
如果这个点非1,那么就自己指向自己,否则指向下一个点,直到遇到自环,有没有感觉非常像并查集?
其实我们只需要路径压缩一下,复杂度O(nlogn)。
这样我们得到了做法:利用并查集暴力枚举每一个非1的数来修改,在修改的同时维护区间最值,最后利用线段树来查询.
例2:传送门
例3:
分析:这道题目的意思是如果u,v的路径只有1种颜色,那么这种颜色的边能联通u,v.我们可以把每个颜色的边给“抽"出来,单独建一个图,然后利用并查集维护连通性,但是如果对于每个图都开一个数组,会有点炸内存啊,10^9的数组可不是说开就能开的,那么怎么做呢?其实可以发现有很多点是孤立的,我们把这些点给排除掉,最后剩下大概2m个点,可是这些点也很多啊,我们能怎么办呢?hash!
因为我们用f[i][j]记录第i个图j的祖先嘛,我们可以用pair+map完美解决,也可以把i和j拼成一个字符串然后用字符串hash,解决一下hash碰撞就好了。
例4:
分析:这道题可以模拟,但是没啥用,因为过不了题......但是因为小球不标号,我们可以这么想:两个小球发生碰撞和两个小球对穿而过是等价的,于是每个球的答案就是xi + vi*t.
例5:
这个题意是错的,原题目为有标号的小球
分析:先看前一组数据,考虑模拟,两个小球相碰撞的情况是方向相反且距离最近,我们把每两队小球碰撞的时间放进一个优先队列,每次处理时间最短的那一个,那么其它的几对小球相撞的时间就要减去第一队所花的时间,还要把新的相撞的小球对放进优先队列里,不过给每一个元素加上这个时间复杂度实在是太高了,我们可以考虑noip蚯蚓那道题的做法:我们把不需要处理的数加上我们原本要减去的数就好了,用一个变量记录我们到底要减去多少,到时候减回来就好了,这是第一组数据的做法.
考虑第二组数据,我们利用例4的做法,我们先给每个小球以坐标大小为依据来编个序号,可以发现,最后下来,这个序号还是这个顺序,也就是说,一开始这个小球是第几个,那么之后他还是第几个,利用这个性质再利用例4的结论,就能A掉此题.
例6:传送门
例7:
分析:因为断言没有矛盾,所以不可能出现一个好人或者坏人说自己是坏人的情况。我们现在考虑几种情况:1.如果A说B是好人,A是好人,那么B是好人。2.如果A说B是好人,A是坏人,那么B是坏人。3.如果A说B是坏人,A是坏人,那么B是好人。4.如果A说B是坏人,A是好人,那么B是坏人。可以看出:如果A说B是好人,不管A是什么,AB都是同类的,如果A说B是坏人,那么两人不同类。那么我们可以利用noip2010关押罪犯的处理方式来用并查集存和自己同一类的,不同类的人。
现在来建图,如果A和B是同类,则从A向B连一条权值为1的无向边,否则连权值为0的,这样我们确定一个起点就能够推出整个连通块的好人坏人数量,有两种可能:(a,b),(b,a).
但是有多个连通块,每个连通块有两种可能,我们要怎么合并答案呢?这个其实非常像背包啊,每个可以取第一个或者取第二个,我们考虑好人的数量,设f[i][j]表示前i个连通块中,有j个好人的方案数,因为有两种组合,可以得到f[i][j] = f[i-1][j - a[i]] + f[i-1][j - b[i]],看最后f[n][p1]是不是等于1就可以了。
因为只用涉及到01运算,所以可以用bool数组优化计算.
例8:
分析:这道题题的题意就是如果u和v只用1条边就连通,那么|xu-xv|就必须≤1,否则就必须≥1
看上去似乎非常难以分析得到答案,我们从最简单的情况来分析:
1.两个点,这个直接弄就好了。
2.三个点,这个有很多方法,比如112,221什么的。
3.四个点: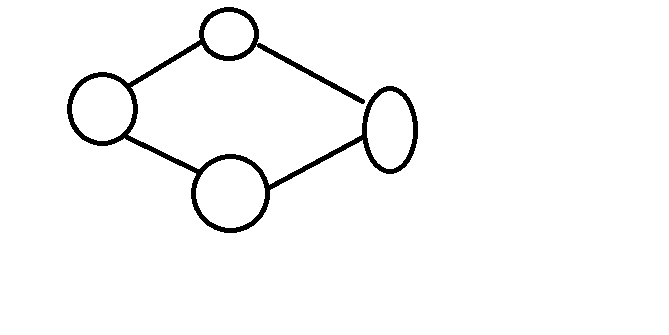
会发现无论怎么样都不能满足要求,但是如果我们在中间加上一笔: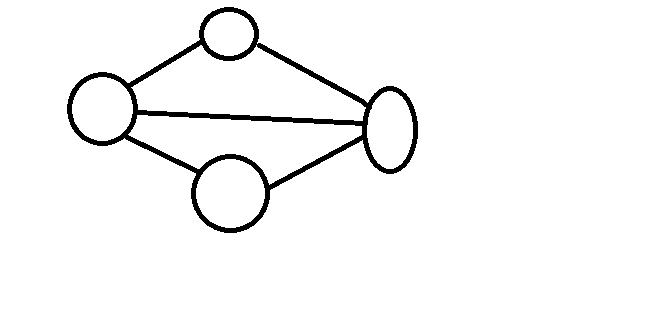
可以发现最左边和最右边填1,上面填2,下面填0就能满足要求,现在我们思考一下,为什么左边和右边的能填成一样的?可以发现,这两个点所连上的点加上自己的集合相等,而上下两个不相等.为什么会这样呢?因为这个集合里保存的都是直接与自己相连的,都满足限制|xu-xv|≤1,如果两个集合不相等,那么就有点不在某个集合内,这个数值就必须要改变。
根据这个性质,我们可以把两个填相同数值的点合并成一个点,可能会出现这样的情况: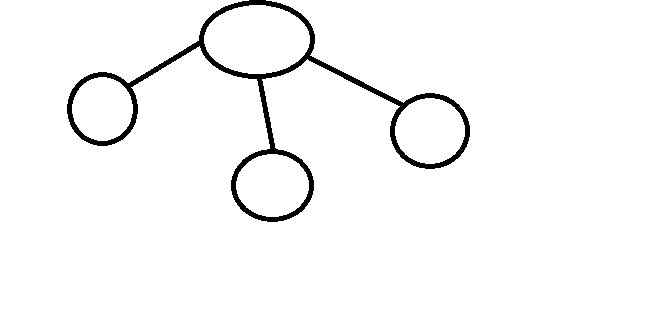
然后我们可以发现,下面的点还可以继续合并,这就与之前的合并矛盾了,所以如果图中存在度数大于等于3的点,那么一定是无解的.
那么接下来就只有两种可能了:环或者链,合并后环是不可能出现的,因为可以继续合并成1个点,那么只有链了,从头到尾依次填0,1,2,3,...,n即可,不过注意我们操作的是合并后的点,记得一定要还原.
例9:
分析:这道题是经典的A*算法的题,A*算法其实和IDA*算法差不多,只不过用优先队列维护,每次估价当前状态到目标状态的可能的值,一般是估优不估劣,如果当前已经用的代价加上估计的代价超过了已有的答案,就不走,这是IDA*,对于A*,我们每次从优先队列中取出已用代价+估计代价的最小的元素来扩展,这里的估价代价就是当前点到终点的最短路,可以先用一次spfa来求,可以知道,这个估价函数是一定估优不估劣的,所以可以用A*算法.
对于怎么求K短路,如果终点被入队了k次,那么求出来的就是k短路。
总体思路就是先倒着做一次spfa,求终点到每个点的最短路来得到估价函数,然后用A*算法来求第k短路。(需要注意的一点是判负环!)
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <queue> using namespace std; int n, m, head[200010], to[200010], nextt[200010], tot, head2[200010], to2[200010], nextt2[200010], tot2, w[200010], w2[200010]; int vis[200010], d[200010],s,t,k,ans; bool flag = true; struct node { int x, dist, f; bool operator < (const node &a) const { if (a.f == f) return a.dist < dist; return a.f < f; } }; void add1(int x, int y, int c) { to[tot] = y; w[tot] = c; nextt[tot] = head[x]; head[x] = tot++; } void add2(int x, int y, int c) { to2[tot2] = y; w2[tot2] = c; nextt2[tot2] = head2[x]; head2[x] = tot2++; } void spfa() { for (int i = 1; i <= n; i++) d[t] = 1000000000; queue <int> q; q.push(t); vis[t] = 1; d[t] = 0; while (!q.empty()) { int u = q.front(); q.pop(); vis[u]--; if (vis[u] > n) { flag = false; return; } for (int i = head2[u]; i + 1; i = nextt2[i]) { int v = to2[i]; if (d[v] > d[u] + w[i]) { d[v] = d[u] + w[i]; if (!vis[v]) { vis[v]++; q.push(v); } } } } } void A_star() { priority_queue <node> q; int cnt = 0; if (s == t) k++; node tmp; tmp.x = s; tmp.dist = 0; tmp.f = d[s]; q.push(tmp); while (!q.empty()) { node u = q.top(); q.pop(); if (u.x == t) cnt++; if (cnt == k) { ans = u.dist; return; } for (int i = head[u.x]; i + 1; i = nextt[i]) { int v = to[i]; node temp; temp.x = v; temp.dist = w[i] + u.dist; temp.f = temp.dist + d[v]; q.push(temp); } } } int main() { memset(head, -1, sizeof(head)); memset(head2, -1, sizeof(head2)); scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); add1(a, b, c); add2(b, a, c); } scanf("%d%d%d", &s, &t, &k); spfa(); if (!flag) printf("-1 "); else { A_star(); printf("%d ", ans); } //while (1); return 0; }
总结:这几道题让我学到了很多东西:
1.在某些情况下,并查集可以代替链表,主要节省的是查找表头的时间
2.存图存不下可以试试hash,对于数字hash在不超时的情况下最好用map或set,万不得已可以转化为字符串求字符串hash,麻烦的是要解决hash碰撞。
3.一些题如果可能很少,我们可以试试推一下每种可能的结论,例如例7
4.从全局分析不出来的题可以试试小范围,并逐步推广到大范围:一般是有一个递推关系或者是数学公式,否则就是不成立.
5.学习了A*算法和怎么求第k短路.推荐一篇博客:传送门