batch
★☆ 输入文件:batch.in 输出文件:batch.out 简单对比
时间限制:1 s 内存限制:128 MB
题目描述
N个任务排成一个序列在一台机器上等待完成(顺序不得改变),这N个任务被分成若干批,每批包含相邻的若干任务。从时刻0开始,这些任务被分批加工,第i个任务单独完成所需的时间是Ti。在每批任务开始前,机器需要启动时间S,而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。每个任务的费用是它的完成时刻乘以一个费用系数Fi。请确定一个分组方案,使得总费用最小。
例如:S=1;T={1,3,4,2,1};F={3,2,3,3,4}。如果分组方案是{1,2}、{3}、{4,5},则完成时间分别为{5,5,10,14,14},费用C={15,10,30,42,56},总费用就是153。
输入格式
第一行是N(1<=N<=5000)。
第二行是S(0<=S<=50)。
下面N行每行有一对数,分别为Ti和Fi,均为不大于100的正整数,表示第i个任务单独完成所需的时间是Ti及其费用系数Fi。
输出格式
一个数,最小的总费用。
输入样例
5
1
1 3
3 2
4 3
2 3
1 4
输出样例
153
额 哇哇哇 dp写挂了 QAQ
正解1
f[i] 前i个任务的最优结果
f[i]=min{f[j] +sumt[i]*(sumc[i]-sumc[j])+S*(sumc[n]-sumc[j])}
好东西呢 唉 QAQ
详细题解如下:
暴力方法
由于每一批任务连续,所以预处理出两个前缀和数组:
sumt[i] 表示 执行前i个任务所需要的时间 , 即t[1]+t[2]+...+t[n]
sumc[i] 表示 不乘时间时,执行前i个任务所需要的费用 , 即c[1]+c[2]+...+c[n]
dp子状态:
dp[i][j] 表示 前i个任务分成j批所需要的最小费用。
于是可以由dp[k][j-1]推出dp[i][j]:
dp[i][j]=min{dp[k][j-1]+(s*j+sumt[i])*(sumc[i]-sumc[k])}
时间复杂度O(n^3),
空间复杂度O(n^2)。
略微优化
暴力方法的dp子状态空间是二维的,由于N <= 10000 ,所以考虑将二维状态降到一维。
将第一维去掉的想法不太实际,故考虑将第二维去掉。
首先思考所有任务都放到同一批中,观察每个任务需要等待S时间的次数:
任务编号 1 2 3 ... n
等待次数 1 1 1 ... 1
当将1~pos1分成一个区间时,每个任务需要等待的次数变为:
任务编号 1 2 3 ... pos1 pos1+1 ... n
等待次数 1 1 1 ... 1 2 ... 2
(如果仍然看不出来,可以再分几次找找规律)
观察等待次数:每次多分出一个区间,区间左端点到n都需要多等待一次S时间。
故可以推出一个新的方程:
dp[i]=min{dp[j]+sumt[i]*(sumc[i]-sumc[j]+s*(sumc[n]-sumc[j]))
dp[i]并不只是前i个的时间 还要加上对后面的影响
上面其实就已经AC了 (但是老师的本意是要让我们写斜率优化)
斜率优化
当每次求dp[i]时,分别整理i,j的信息,把原来的方程进行玄学变形(移项):
dp[i]=min{dp[j]-(s+sumt[i])*sumc[j]}+sumt[i]*sumc[i[]+s*sumc[n]
去掉min函数,把dp[j]和sumc[j]看作变量,整理出dp[j]关于sumc[j]的一次函数(重要!):
dp[j]=(s+sumt[i]) * sumc[j] + (dp[i]-sumt[i]*sumc[i]-s*sumc[n])
y = k * x + b
其中sumc[j]是自变量,dp[j]是因变量,s+sumt[i]是斜率,后面一串为截距。
建立一个平面直角坐标系:
每个决策j的二元组(sumc[j] , dp[j])表示坐标系中的点。
当前状态dp[i]表示直线的截距(且这条直线斜率为s+sumt[i])。
令直线过每个点可以得到解出截距,使截距最小的就是最优决策。
如图:
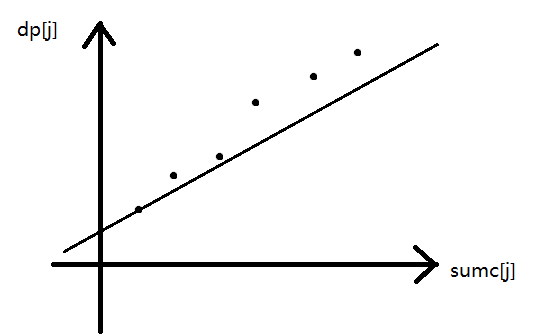
讨论三个决策点j1,j2,j3(j1<j2<j3)对应的坐标系中的点:
第一种情况:上凸。用眼睛观察(hhh)可知,j2此时不可能成为最佳决策点,故放弃。
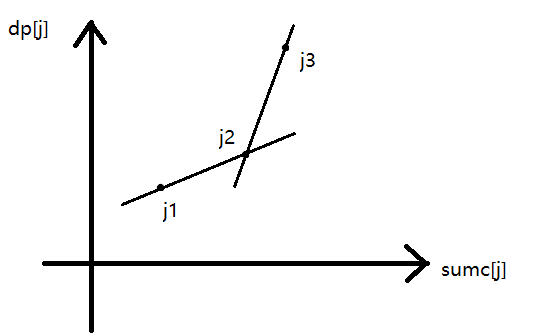
第二种情况:下凹。此时j2有可能成为最佳决策点。
最后把所有可能成为最佳决策点的j处理出来,即维护一个相邻点斜率单调递增的“凸壳”。
其中最佳决策点左端斜率<s+sum[i],右端斜率>s+sum[i](可以证明这样的点只有一个)。
又因为s+sumt[i]是单调递增的,所以可以用单调队列找第一个右端斜率>s+sum[i]的点。
总时间复杂度:循环递推O(n)+单调队列O(n)=O(n)。
空间复杂度:一维状态O(n)。
#include <stdio.h> typedef long long ll; typedef double db; const int N=1e6+10; int n,S,s[N],t[N],q[N],head,tail; ll dp[N],val[N]; db k(int j,int k){return (db)(val[j]-val[k])/(s[j]-s[k]);} int main() { freopen("batch.in","r",stdin); freopen("batch.out","w",stdout); scanf("%d%d",&n,&S); for (int i=1;i<=n;i++){ scanf("%d%d",&t[i],&s[i]); t[i]+=t[i-1]; s[i]+=s[i-1]; } q[head=tail=1]=0; for (int i=1;i<=n;i++){ for (;head<tail&&k(q[head],q[head+1])<S+t[i];head++); int j=q[head]; dp[i]=dp[j]+ll(s[n]-s[j])*(S+t[i]-t[j]); val[i]=dp[i]+(ll)s[i]*t[i]-(ll)s[n]*t[i]; for (;head<tail&&k(q[tail-1],q[tail])>k(q[tail],i);tail--); q[++tail]=i; } printf("%lld ",dp[n]); return 0; }
N^2暴力AC!
#include<bits/stdc++.h> #define maxn 5005 using namespace std; int t[maxn],f[maxn],sumt[maxn],sumf[maxn],dp[maxn]; int main(){ // freopen("batch.in","r",stdin);freopen("batch.out","w",stdout); int n,s;scanf("%d%d",&n,&s); for(int i=1;i<=n;i++) scanf("%d%d",&t[i],&f[i]); for(int i=1;i<=n;i++) sumt[i]=sumt[i-1]+t[i],sumf[i]=sumf[i-1]+f[i]; memset(dp,0x3f,sizeof(dp)); // dp[1]=t[1]*f[1]+s*(sumf[n]-sumf[1]); dp[0]=0; for(int i=1;i<=n;i++) for(int j=0;j<i;j++) dp[i]=min(dp[i],dp[j]+sumt[i]*(sumf[i]-sumf[j])+s*(sumf[n]-sumf[j])); printf("%d",dp[n]); //f[i]=min{f[j] +sumt[i]*(sumc[i]-sumc[j])+S*(sumc[n]-sumc[j])} return 0; }