【学习笔记】树上启发式合并 概念+基础运用

引入

现在考虑这样一类树上统计问题：

• 无修改操作，询问允许离线

• 对子树信息进行统计（链上的信息在某些条件下也可以统计

用什么来做呢？暴力？树上差分？树上莫队？

今天要介绍的这种算法 将吊打以上

有请它闪亮登场——dsu on tree！！！

看到这个名字，嗯？dsu？不是并查集嘛（至少我第一眼是这么想的），树上并查集？
其实它和并查集没有半毛钱关系，用dsu这个名字可能只是因为它和并查集都运用了一种思想——启发式合并

什么意思呢？还记得我们并查集的按秩合并吗？

在这个合并的过程中 我们把小的集合合并到了大集合中去

同样的 树上启发式合并实际就是把一棵高度小的子树合并到了大的子树去，这样的一个优化。

算法内容

先思考下面这个问题

给定一棵树 树的每个结点都有一个确定的颜色，询问一些子树的颜色数量（颜色可以重复）

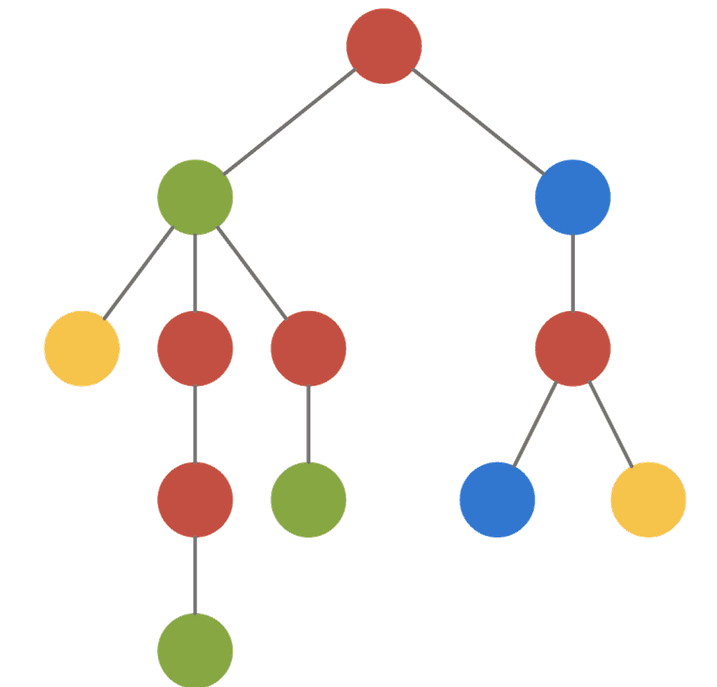
我们先想想O（N²）的暴力做法

对于每个节点，暴力遍历子树，将它们的数据统计出来得到当前节点的答案，然后再暴力将这棵子树的数据清空，以免影响到别的节点。

由于空间的限制，我们不可能对于每一个节点开一个数组来记录数据，只能开一个全局数组。
在这个全局数组内，如果不清空，就会影响到别的子树，答案混淆于是导致WA

但是可以发现，统计儿子节点时最后那个节点其实没有必要清空，因为它不再会影响到它的兄弟节点。那么该如何优化呢？

轻重链剖分优化

对于节点x，可以在做子树答案时保留最后一棵子树u的数据不清空，然后统计x的答案时绕过u节点统计别的子树。那么u选哪个呢？注意我们是选择一个

子树来保存答案，对于其他的非重儿子进行暴力，为了复杂度最优，当然是选子树个数多的咯
于是我们可以通过重儿子进行算法优化。

可以发现，每个节点的答案由其子树和其本身得到，考虑利用这个性质处理问题。

首先我们可以先预处理出每个节点子树的size和它的重儿子，重儿子同树链剖分一样，是拥有节点最多子树的儿子，这个过程显然可以O(n)完成

接下来，对于每一个结点，我们按照这样的方式进行遍历

• 遍历所有轻儿子，递归结束时消除它们的贡献

• 遍历所有重儿子，保留它的贡献

• 再计算当前子树中所有轻子树的贡献

• 更新答案

• 如果当前点是轻儿子，消除当前子树的贡献

这样，对于一个节点，我们遍历了一次重子树，两次非重子树，显然是最划算的。

通过执行这个过程，我们获得了这个节点所有子树的 ans

思路已经很清晰了，通过这样的优化，最终的时间复杂度我们发现应该为那么总复杂度就是 O (n log ⁡n)的

最主要的原因

• 根据树链剖分相关理论，每个点到根的路径上有logn条重链与logn条轻链
• 即一个点的信息只会上传logn次（详细证明暂且不写，如需可查阅其他大佬证明）

大致的代码如下所示（随便口糊的，不要真的去测，有个思路就好）

预处理：

inline void dfs1(int x,int fa){
    size[x]=1;
    //depth 
    for(int i=head[x];i;i=t[i].nxt){
        int to=t[i].to;
        if(to!=fa){
            dfs1(to,x);
            size[x]+=size[to];
            if(size[to]>size[son[x]])
                son[x]=to;
        }
    }
}//dfs预处理 

求ans

inline int dfs2(int u,int fa,int isson,int keep){
    if(keep){
        for(int i=head[u];i;i=t[i].nxt){
            int to=t[i].to;
            if(to!=fa&&to!=son[u]){
                dfs2(to,u,0,1);
            }
        }
    }
    int tmp=0;
    if(!keep&&son[u])tmp+=dfs2(son[u],u,1,0);
    else if(son[u]) tmp+=dfs2(son[u],u,1,1);
    for(int i=head[u];i;i=t[i].nxt){
        int v=t[i].to;
        if(v!=fa&&v!=son[u]){
            tmp+=dfs2(v,u,0,0);
        }
    }
    if(!cnt[c[u]]){
        tmp++;
    }
    cnt[c[u]]++;
    if(keep)ans[u]=tmp;
    if(keep&&!isson) memset(cnt,0,sizeof(cnt));
    return tmp;
}

练习

给一些很不错的例题

$$\text{CF600E Lomsat gelral}$$

$$\text{UOJ284 快乐游戏鸡}$$

$$\text{树上数颜色}$$

CF208E Blood Cousins

CF570D Tree Requests

CF246E Blood Cousins Return

U95602 射手座之日