在一堆介绍卷积的帖子中，这篇特别之处在于很萌的示例配色，令人眼前一亮，当然直观也是很直观滴，保证了能在昏昏欲睡见周公子前看完。
https://towardsdatascience.com/types-of-convolution-kernels-simplified-f040cb307c37
直观介绍各种迷人的CNN层
一个简短的介绍
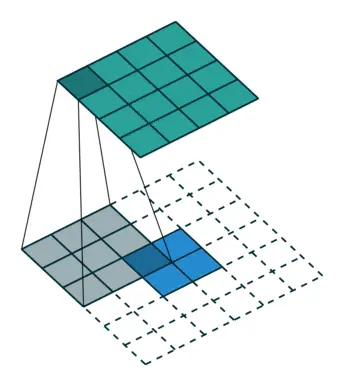
卷积使用“kernel”从输入图像中提取某些“特征”。kernel是一个矩阵，可在图像上滑动并与输入相乘，从而以某种我们期望的方式增强输出。看下面的GIF。
上面的kernel可用于锐化图像。但是这个kernel有什么特别之处呢？考虑下图所示的两个输入图像。第一个图像，中心值为3 * 5 + 2 * -1 + 2 * -1 + 2 * -1 + 2 * -1 =7，值3增加到7。第二个图像，输出是1 * 5 + 2 * -1 + 2 * -1 + 2 * -1 + 2 * -1 = -3，值1减少到-3。显然，3和1之间的对比度增加到了7和-3，图像将更清晰锐利。
通过深层 CNN，我们无需再用手工设计的kernel来提取特征，而是可以直接学习这些可提取潜在特征的kernel值。
Kernel与Filter
在深入探讨之前，我想先明确区分“kernel”和“filter”这两个术语，因为我已经看到很多人把它们混为一谈。如前所述，kernel是权重矩阵，将权重矩阵与输入相乘以提取相关特征。卷积名称就是kernel矩阵的维数。例如，2D卷积的kernel矩阵就是2D矩阵。
但是，filter是多个kernel的串联，每个kernel分配给输入的特定通道。filter总是比kernel大一维。例如，在2D卷积中，filter是3D矩阵（本质上是2D矩阵（即kernel）的串联）。因此，对于具有kernel尺寸h * w和输入通道k的CNN层，filter尺寸为k * h * w。
一个普通的卷积层实际上由多个这样的filter组成。为了简化下面的讨论，除非另有说明，否则假定仅存在一个filter，因为所有filter都会重复相同的操作。
1D，2D和3D卷积
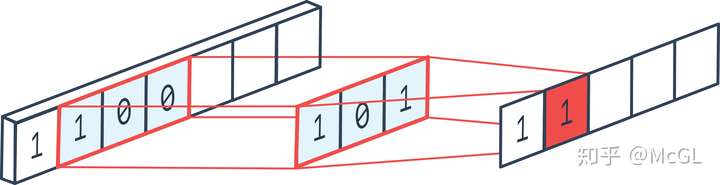
一维卷积通常用于时间序列数据分析（因为这种情况下的输入为一维）。如前所述，一维数据输入可以具有多个通道。滤波器只能沿一个方向移动，因此输出为1D。参见下面的单通道一维卷积示例。
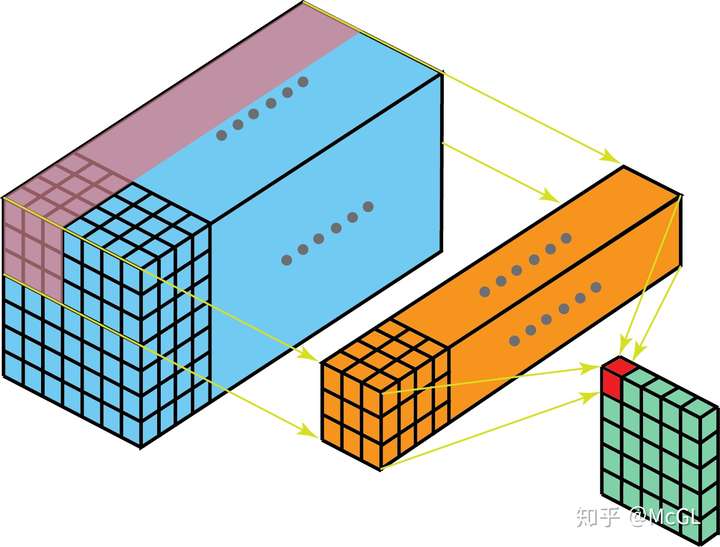
我们已经在帖子的开头看到了一个单通道2D卷积的示例，因此让我们可视化一个多通道2D卷积，并尝试理解它。在下图中，kernel尺寸为3 * 3，并且filter中有多个这样的kernel（标记为黄色）。这是因为输入中有多个通道（标记为蓝色），并且我们有一个kernel对应于输入中的每个通道。显然，这里的filter可以在两个方向上移动，因此最终输出是2D。2D卷积是最常见的卷积，在计算机视觉中大量使用。
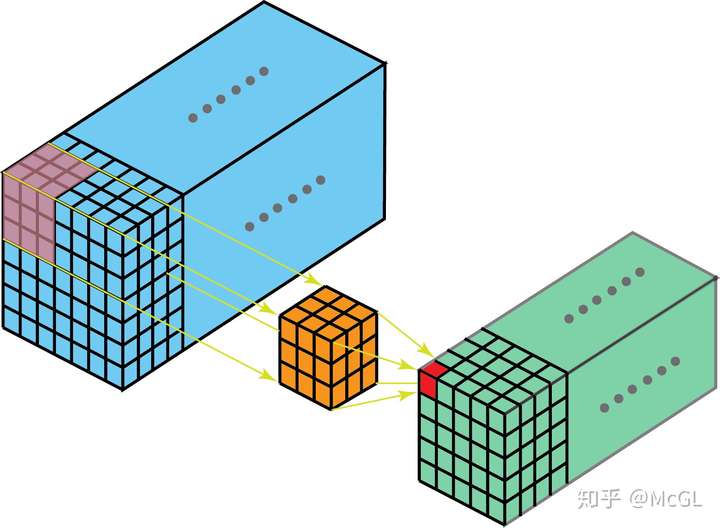
很难可视化3D filter（因为它是4D矩阵），因此我们在这里只讨论单通道3D卷积。如下图所示，在3D卷积中，kernel可以在3个方向上移动，因此获得的输出也是3D。
在修改和自定义CNN层方面所做的大多数工作都只集中在2D卷积上，因此从现在开始，我只讨论2D卷积的变种。
转置(Transposed)卷积
下面的GIF很好的记录了2D卷积如何减小输入的尺寸。但是有时我们需要对输入进行如增加尺寸（也称为“上采样”）等处理。
为了使用卷积实现此目标，我们使用了称为转置卷积或反卷积（它并不是真正的“逆转”卷积运算，所以很多人不喜欢使用反卷积这个术语）的卷积修改版。下面的GIF中的虚线块表示padding。
这些动画很直观的展示了如何基于不同的padding模式从同一输入产生不同的上采样输出。这种卷积在现代CNN网络中非常常用，主要是因为它们具有增加图像尺寸的能力。
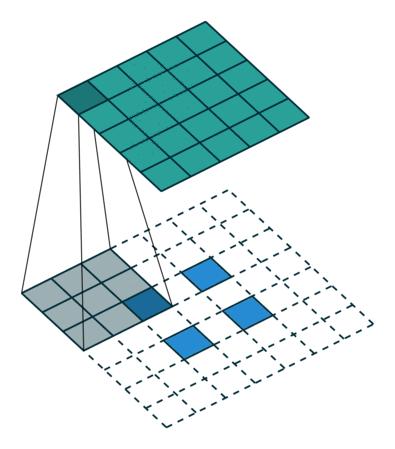
可分离卷积
可分离卷积是指将卷积kernel分解为低维kernel。可分离卷积有两种主要类型。首先是空间上可分离的卷积，如下
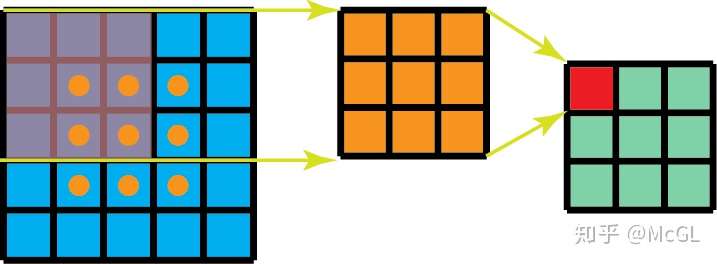标准的2D卷积核
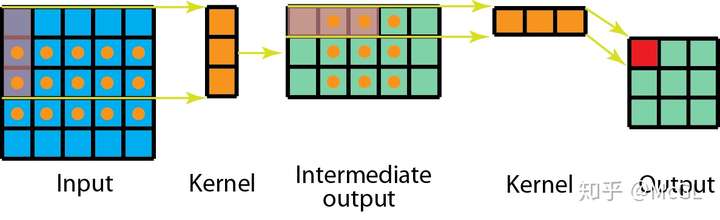空间可分离的2D卷积
空间可分离的卷积在深度学习中并不常见。但是深度可分离卷积被广泛用于轻量级CNN模型中，并提供了非常好的性能。参见以下示例。
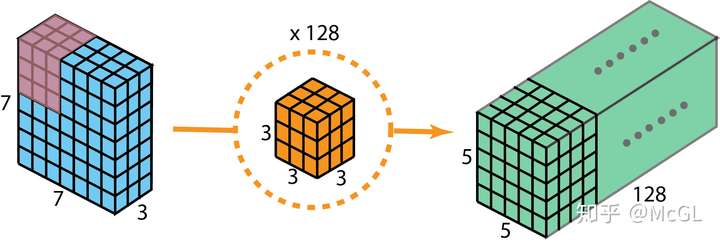具有2个输入通道和128个filter的标准2D卷积
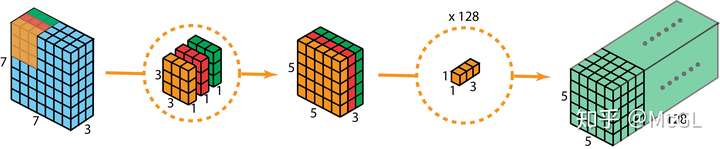深度可分离的2D卷积，它首先分别处理每个通道，然后进行通道间卷积
但是为什么用可分离的卷积呢？效率！！使用可分离卷积可以显著减少所需参数的数量。随着当今我们的深度学习网络的复杂性不断提高和规模越来越大，迫切需要以更少的参数提供相似的性能。
扩张/空洞(Dilated/Atrous)卷积
如你在以上所有卷积层中所见，无一例外，它们将一起处理所有相邻值。但是，有时跳过某些输入值可能更好，这就是为什么引入扩张卷积（也称为空洞卷积）的原因。这样的修改允许kernel在不增加参数数量的情况下增加其感受野。
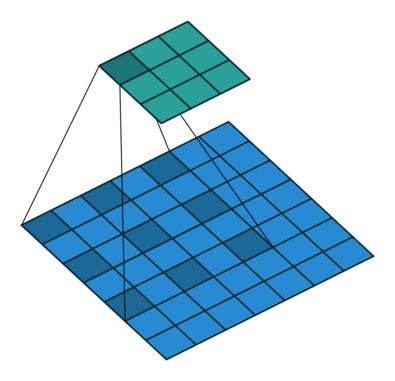
显然，可以从上面的动画中注意到，kernel能够使用与之前相同的9个参数来处理更广阔的邻域。这也意味着由于无法处理细粒度的信息（因为它跳过某些值）而导致信息丢失。但是，在某些应用中，总体效果是正面的。
可变形(Deformable)卷积
就特征提取的形状而言，卷积非常严格。也就是说，kernel形状仅为正方形/矩形（或其他一些需要手动确定的形状），因此它们只能在这种模式下使用。如果卷积的形状本身是可学习的呢？这是引入可变形卷积背后的核心思想。
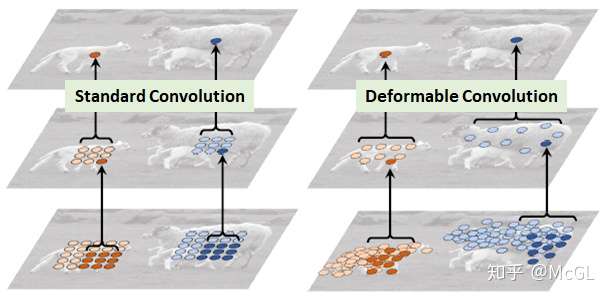
实际上，可变形卷积的实现非常简单。每个kernel都用两个不同的矩阵表示。第一分支学习从原点预测“偏移”。此偏移量表示要处理原点周围的哪些输入。由于每个偏移量都是独立预测的，它们之间无需形成任何刚性形状，因此具有可变形的特性。第二个分支只是卷积分支，其输入是这些偏移量处的值。
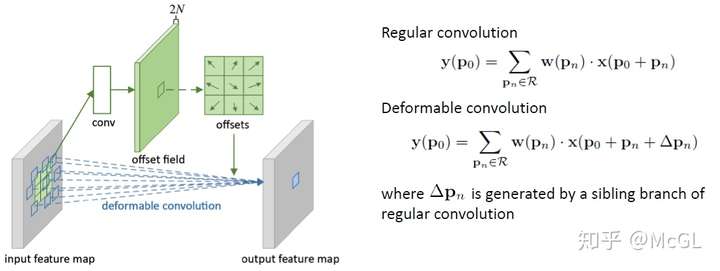
What's next？
CNN层有多种变体，可以单独使用或彼此结合使用以创建成功且复杂的体系结构。每个变化都是基于特征提取应如何工作的直觉而产生的。因此，尽管这些深层CNN网络学到了我们无法解释的权重，但我相信产生它们的直觉对于它们的性能非常重要，朝着这个方向进行进一步的研究工作对于高度复杂的CNN的成功至关重要。