遗传算法（Genetic Algorithm）

求函数f(x) = xsin(10Π·x) + 2.0 x∈[-1,2]的最大值：

一、编码

设求解精度精确到6位小数，所以将区间 [-1,2] 分为 [2-(-1)]×10⁶ = 3×10⁶ 等份
2²¹ < 3×10⁶ < 2²²
所以编码的二进制串长至少22位
二进制串 s = (b₂₁b₂₀…b₀)，如 <1000101110110101000111>
x'= s对应的十进制，如 (1000101110110101000111)₂ = 2 288 967
x = 对应的[-1,2]中的值，如 -1 + 2288967 × 3 / (2²² - 1) = 0.637 197

二、产生初始种群

设产生了4个初始个体
s1 = <1000101110110101000111>
s2 = <0000001110000000100000>
s3 = <1110000000111111000101>
s4 = <0010001000110111010010>

三、计算适应度

令 适应值函数 f(s) = 目标函数 f(x)

编号	个体串	x	适应值	百分比/%	累计百分比/%
s1	1000101110110101000111	0.637 197	2.586 364	29.1	29.1
s2	0000001110000000100000	-0.958 373	1.078 878	12.1	41.2
s3	1110000000111111000101	1.627 888	3.250 650	36.5	77.7
s4	0010001000110111010010	-0.599 032	1.981 785	22.3	100

s₃的适应值最大，为最佳个体

四、遗传操作

1.选择
转盘赌方式：

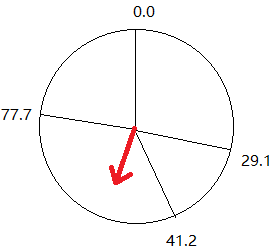
生成随机数0.35、0.72，所以选中的个体为s₂、s₃

2.交叉
s₂ = <0000001110000000100000>
s₃ = <1110000000111111000101>
随机选择交叉点，如第5位与第6位之间，交叉后产生子个体：
s₂' = <00000|00000111111000101>
s₃' = <11100|01110000000100000>
适应值为：
f(s₂') = f(-0.998 113) = 1.940 865
f(s₃') = f(1.666 028) = 3.459 245
交叉后，子个体s₃'的适应值比父个体高

3.变异
若以一小概率选择了s₃的第5个遗传因子变异，产生的新个体为：
s₃' = <1110__1__00000111111000101>
适应值为：
f(s₃') = f(1.721 638) = 0.917 743

五、模拟结果

令种群大小为50，交叉概率 p_c = 0.25，变异概率 p_m = 0.01
按照标准遗传算法SGA，运行到第89代时获得的最佳个体为：
s_max = <1111001100111111001011>
x_max = 1.850 549
f(x_max) = 3.850274

---

参考：https://www.jianshu.com/p/ae5157c26af9