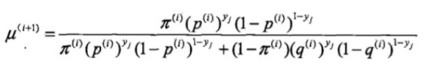EM算法之Python

转载之：https://zhuanlan.zhihu.com/p/31345125

示例一：二硬币模型

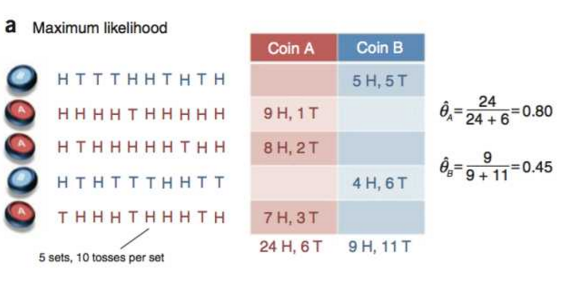
假设现在有两个硬币A和B，我们想要知道两枚硬币各自为正面的概率啊即模型的参数。我们先随机从A,B中选一枚硬币，然后扔10次并记录下相应的结果，H代表正面T代表反面。对以上的步骤重复进行5次。如果在记录的过程中我们记录下来每次是哪一枚硬币（即知道每次选的是A还是B），那可以直接根据结果进行估计（见下图a）。

不含隐变量的参数求解问题

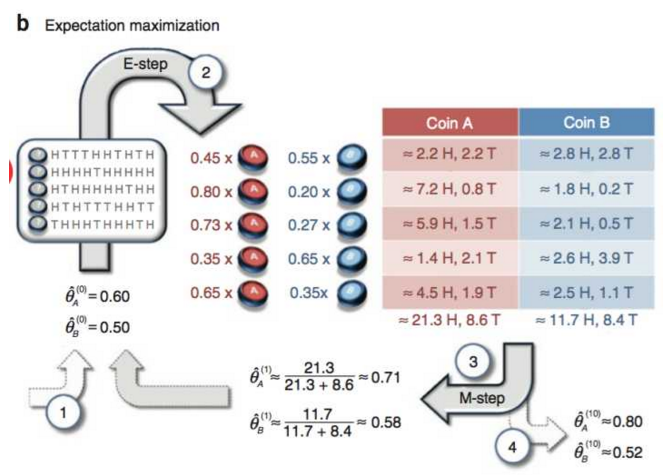
但是如果数据中没记录每次投掷的硬币是A还是B（隐变量），只观测到5次循环共50次投币的结果，这时就没法直接估计A和B的正面概率。这时就该轮到EM算法大显身手了，EM算法特别适用于这种含有隐变量的参数求解问题（见下图b）。

含有隐变量的参数求解

先初始化输入参数，如上图1步给了一个初始值0.6（A硬币正面的概率），0.5（B硬币正面的概率）。接下来先进行E步（对隐变量求期望），如上图2步：以第一条数据为例，5H5T，为A的概率为  ,为B的概率  ，归一化后得P(A)=0.45,P(B)=0.55,剩下几条数据同理可得。而后通过M-step可计算重新迭代的概率值。如上图第一次迭代后  ，循环上面的E、M步骤直至收敛我们就可以得到最终的答案，如上图进过10次迭代后得到了最终的结果。

---

示例二：三硬币模型

现在我们将上面的二硬币模型扩展为三硬币模型，其实原理基本差不多。假设有三枚硬币A、B、C，这些硬币正面出现的概率分别p，q和  。先抛C硬币，如果C硬币为正面则选择硬币A，反之选择硬币B，然后对选出的硬币进行一组实验，独立的抛十次。共做5次实验，每次实验独立的抛十次，结果如图中a所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H，H代表正面朝上。

5次实验结果

本人最近也刚学EM算法，下面代码主要参考EM算法及其推广，这里面作者实现了一个两硬币模型的EM算法。本文对其稍做了一点修改，变成三硬币模型。

EM算法步骤：

E步：计算在当前迭代的模型参数下，观测数据y来自硬币B的概率：

M步：估算下一个迭代的新的模型估算值

对于这个三硬币模型来说，我们先通过E步（对隐变量求期望）来求得隐变量的参数（即属于哪个硬币），然后再通过M-step来重新估算三个硬币的参数，直至收敛（达到要求）为止。下面是实现三硬币模型的EM算法代码，希望可以更好的帮助理解。

# !usr/bin/env python
# -*- coding:utf-8 -*-
import numpy as np
from scipy import stats

def em_single(priors, observations):
    """
    EM算法单次迭代
    Arguments
    ---------
    priors : [theta_A, theta_B，theta_C]
    observations : [m X n matrix]

    Returns
    --------
    new_priors: [new_theta_A, new_theta_B,new_theta_C]
    :param priors:
    :param observations:
    :return:
    """
    counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}}
    theta_A = priors[0]
    theta_B = priors[1]
    theta_c=priors[2]
    # E step
    weight_As=[]
    for observation in observations:
        len_observation = len(observation)
        num_heads = observation.sum()
        num_tails = len_observation - num_heads
        contribution_A = theta_c*stats.binom.pmf(num_heads, len_observation, theta_A)
        contribution_B = (1-theta_c)*stats.binom.pmf(num_heads, len_observation, theta_B)  # 两个二项分布
        weight_A = contribution_A / (contribution_A + contribution_B)
        weight_B = contribution_B / (contribution_A + contribution_B)
        # 更新在当前参数下A、B硬币产生的正反面次数
        weight_As.append(weight_A)
        counts['A']['H'] += weight_A * num_heads
        counts['A']['T'] += weight_A * num_tails
        counts['B']['H'] += weight_B * num_heads
        counts['B']['T'] += weight_B * num_tails
    # M step
    new_theta_c = 1.0*sum(weight_As)/len(weight_As)
    new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
    new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
    return [new_theta_A, new_theta_B,new_theta_c]

def em(observations, prior, tol=1e-6, iterations=10000):
    """
    EM算法
    :param observations: 观测数据
    :param prior: 模型初值
    :param tol: 迭代结束阈值
    :param iterations: 最大迭代次数
    :return: 局部最优的模型参数
    """
    import math
    iteration = 0
    while iteration < iterations:
        new_prior = em_single(prior, observations)
        delta_change = np.abs(prior[0] - new_prior[0])
        if delta_change < tol:
            break
        else:
            prior = new_prior
            iteration += 1
    return [new_prior, iteration]

# 硬币投掷结果观测序列：1表示正面，0表示反面。
observations = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1],
                         [1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
                         [1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
                         [1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
                         [0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])

print em(observations, [0.5, 0.8, 0.6])

运行后结果为：

[[0.51392121603987106, 0.79337052912023864, 0.47726196801164544], 42]

从结果我们可以了解到经过42轮迭代，我们最终得出了结果：硬币A正面的概率为0.51392121603987106，硬币B为正面的概率为0.79337052912023864，C硬币正面概率为0.47726196801164544。

至此EM算法的实现就完成了