矩阵问题

一、转圈打印矩阵

【题目】

　　给定一个整型矩阵matrix，请按照转圈的方式打印它。例如：

　　

　　打印结果为：1，2，3，4，8，12，16，15，14，13，9，5，6，7，11， 10

　　

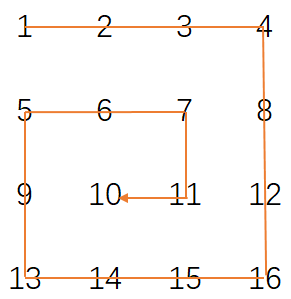
　　要求：额外空间复杂度为O(1)。

【分析】

　　用4个变量来标记左上角的点和右下角的点。

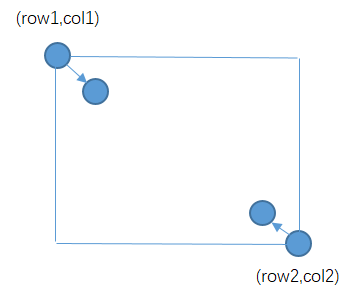
　　如果要打印这2个点形成矩阵的边界，可以写一个函数，具体是：col1++，加到col2的位置停止，然后row1++，加到row2的位置停止；然后row2--，减到row1停；col2--,减到col1停止

　　          　　

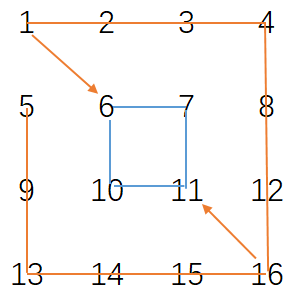
　　打印完最外层的1圈后，左上角的点往右下方移动，右下角的点往左上方移动；当row1>row2或col1>col2时流程结束

　　　　　　

【代码实现】

public class PrintMatrixSpiralOrder {

    public static void spiralOrderPrint(int[][] matrix) {
        int row1 = 0;
        int col1 = 0;
        int row2 = matrix.length - 1;
        int col2 = matrix[0].length - 1;
        while (row1 <= row2 && col1 <= col2) {
            printEdge(matrix, row1++, col1++, row2--, col2--);
        }
    }

    public static void printEdge(int[][] m, int row1, int col1, int row2, int col2) {
        //如果这个矩阵只有1行数
        if (row1 == row2) {
            //打印这一行
            for (int i = col1; i <= col2; i++) {
                System.out.print(m[i][col1] + " ");
            }
            //如果这个矩阵只有1列
        } else if (col1 == col2) {
            //打印这一列
            for (int i = row1; i <= row2; i++) {
                System.out.print(m[i][col1] + " ");
            }
            //如果是多乘多的矩阵
        } else {
            int curC = col1;
            int curR = row1;
            while (curC != col2) {
                System.out.print(m[row1][curC] + " ");
                curC++;
            }
            while (curR != row2) {
                System.out.print(m[curR][col2] + " ");
                curR++;
            }
            while (curC != col1) {
                System.out.print(m[row2][curC] + " ");
                curC--;
            }
            while (curR != row1) {
                System.out.print(m[curR][col1] + " ");
                curR--;
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12},
                {13, 14, 15, 16}};
        spiralOrderPrint(matrix);
    }
}

二、旋转正方形矩阵

【题目】

　　给定一个整型正方形矩阵matrix，请把该矩阵调整成顺时针旋转90度的样子。
　　要求： 额外空间复杂度为O(1)。

【分析】

　　在给定的正方形中，先转最外圈，再转里面的。如果能保证最外层的数能转对，里面再依次转完即可。
　　举个例子：

　　

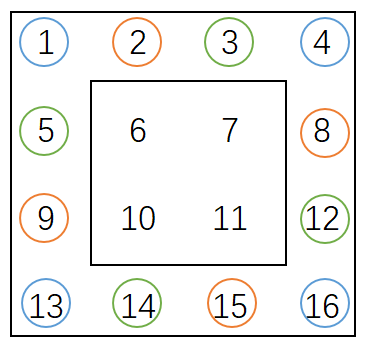
　　如果能把最外1圈的数转对，再转里面1圈(6,7,10,11)，那么整体就旋转成功了。
　　先看最外1圈，从1开始，1、4、16、13之间相互交换位置，即1→4，4→16，16→13，13→1。
　　然后从2开始，2、8、15、9之间交换位置。再看第三组，3、12、14、5之间交换位置。

【代码实现】

public class RotateMatrix {
    public static void rotate(int[][] matrix) {
        int row1 = 0;
        int col1 = 0;
        int row2 = matrix.length - 1;
        int col2 = matrix[0].length - 1;
        while (row1 < row2) {
            rotateEdge(matrix, row1++, col1++, row2--, col2--);
        }
    }

    /**
     * 左上角的(row1,col1)和右下角的(row2,col2)一定要组成一个正方形,这是调用此函数的前提
     *
     * @param m
     * @param row1 左上角的行号
     * @param col1 左上角的列号
     * @param row2 右下角的行
     * @param col2 右下角的列
     */
    public static void rotateEdge(int[][] m, int row1, int col1, int row2, int col2) {
        int times = col2 - col1;
        int tmp = 0;
        //从1出发,1、4、16、13之间相互交换位置,直至
        for (int i = 0; i < times; i++) {
            tmp = m[row1][col1 + i];
            m[row1][col1 + i] = m[row2 - i][col1];
            m[row2 - i][col1] = m[row2][col2 - i];
            m[row2][col2 - i] = m[row1 + i][col2];
            m[row1 + i][col2] = tmp;
        }
    }

    public static void printMatrix(int[][] matrix) {
        for (int i = 0; i != matrix.length; i++) {
            for (int j = 0; j != matrix[0].length; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                { 13, 14, 15, 16 } };
        printMatrix(matrix);
        rotate(matrix);
        System.out.println("=========");
        printMatrix(matrix);
    }
}

三、“之”字形打印矩阵

【题目】

　　给定一个矩阵matrix，按照“之”字形的方式打印这个矩阵，例如： 1 2 3 4 5 6 7 8 9 10 11 12

　　

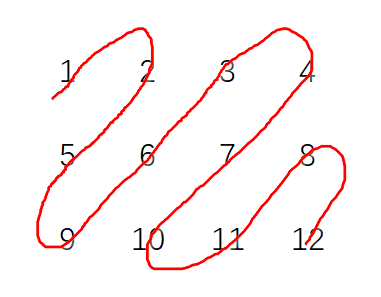
　　“之”字形打印的结果为：1，2，5，9，6，3，4，7，10，11，8，12
　　要求：额外空间复杂度为O(1)。

【分析】

　　如果把思路限制在1怎么变到2，2怎么变到5，5怎么变到9。。。这样是很愚蠢的！

　　我们应该这样想：

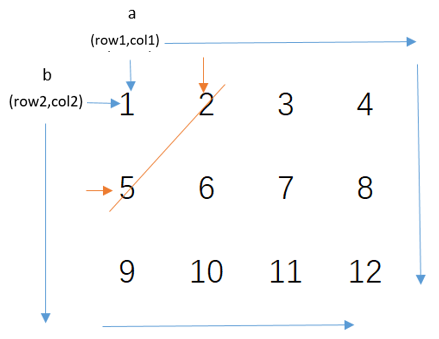
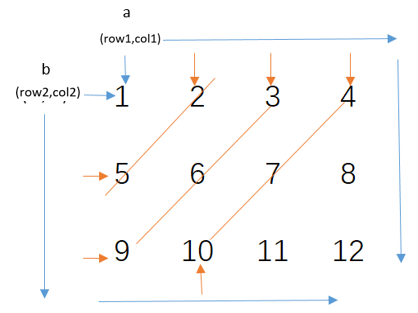
　　有一个(row1,col1)，记为a点、(row2,col2)，记为b点，一开始指向1的位置，并打印它。每次打印完后，a向右移动，移动到最右边后向下移动；b先向下移动，到最下方后再往右移动。

　　当a移动到2，b移动到5时，a、b两点可形成1条对角线；当a移动到3，b移动到9时，两点间也可以形成一条对角线；a移动到4，b移动到10时，又是1条对角线。。。

　                　　

【代码实现】

public class ZigZagPrintMatrix {

    public static void printMatrixZigZag(int[][] matrix) {
        int row1 = 0;
        int col1 = 0;
        int row2 = 0;
        int col2 = 0;
        int endR = matrix.length - 1;
        int endC = matrix[0].length - 1;
        boolean fromUp = false;
        //当row1没走到结尾
        while (row1 != endR + 1) {
            printLevel(matrix, row1, col1, row2, col2, fromUp);
            //到col1触到最后1列时,row1才开始增加
            row1 = col1 == endC ? row1 + 1 : row1;
            //如果col1已经到最后,就不变,否则col1增加
            col1 = col1 == endC ? col1 : col1 + 1;
            col2 = row2 == endR ? col2 + 1 : col2;
            row2 = row2 == endR ? row2 : row2 + 1;
            //对角线交替着打印
            fromUp = !fromUp;
        }
        System.out.println();
    }

    /**
     * (row1,col1)和(row2,col2)两个点连起来一定是一条对角线,这个函数就是打印对角线上的元素
     * 并且这个函数可以实现从左下方到右上方打印,也可以实现从右上方到左下方的打印
     * @param m
     * @param row1
     * @param col1
     * @param row2
     * @param col2
     * @param fromUp 控制对角线打印的方向。true:右上方到左下方   false:左下方到右上方
     */
    public static void printLevel(int[][] m, int row1, int col1, int row2, int col2, boolean fromUp) {
        //fromUp为true时,从右上方到左下方依次打印对角线上的元素
        if (fromUp) {
            //row1 != row2 + 1等价于row1<=row2
            while (row1 != row2 + 1) {
                System.out.print(m[row1++][col1--] + " ");
            }
            //fromUp为false时,从左下方到右上方依次打印对角线上的元素
        } else {
            while (row2 != row1 - 1) {
                System.out.print(m[row2--][col2++] + " ");
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
        printMatrixZigZag(matrix);
    }
}

四、在行列都排好序的矩阵中找数

【题目】

　　给定一个有N*M的整型矩阵matrix和一个整数K，matrix的每一行和每一 列都是排好序的。实现一个函数，判断K是否在matrix中。 例如：

　　

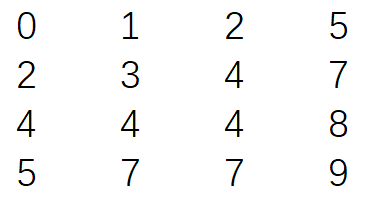
　　如果K为7，返回true；如果K为6，返回false。
　　要求：时间复杂度为O(N+M)，额外空间复杂度为O(1)。

【分析】

　　如果通过遍历的方式，一共N*M个数，每个数都遍历，时间复杂度就是O(N*M)，显然不符合要求。

　　通过例子来分析这个题目：

　　

　　如果要判断6是否在上面的矩阵中，可以从右上角9开始查，9>6，因为每一列都是有序的，所以9这列底下的数一定没有6；

　　

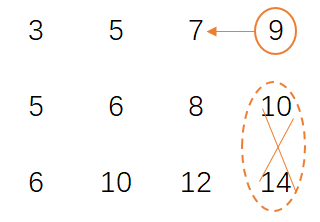
　　然后从9向左移动，来到7的位置，7>6，所以7底下的数一定没有6

　　

　　继续从7往左移动，来到5的位置，5<6，所以5的左边一定比6小，于是从5往下走，来到6的位置，返回true

　　

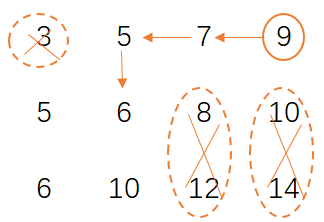
　　总结就是：从右上角开始，当前数大于要找的数，向左移动；当前数小于要找的数，向下移动；当前数如果等于要找的数，返回true；如果走到越界的位置还没找到，一定不存在，返回false。

　　注意：从左下角开始找也是可以的。但是不能从左上角或右下角开始找！

【代码实现】

public class FindNumInSortedMatrix {
    public static boolean isContains(int[][] matrix, int K) {
        int row = 0;
        int col = matrix[0].length - 1;
        while (row < matrix.length && col > -1) {
            if (matrix[row][col] == K) {
                return true;
            } else if (matrix[row][col] > K) {
                col--;
            } else {
                row++;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] matrix = new int[][]{{0, 1, 2, 3, 4, 5, 6},// 0
                {10, 12, 13, 15, 16, 17, 18},// 1
                {23, 24, 25, 26, 27, 28, 29},// 2
                {44, 45, 46, 47, 48, 49, 50},// 3
                {65, 66, 67, 68, 69, 70, 71},// 4
                {96, 97, 98, 99, 100, 111, 122},// 5
                {166, 176, 186, 187, 190, 195, 200},// 6
                {233, 243, 321, 341, 356, 370, 380} // 7
        };
        int K = 233;
        System.out.println(isContains(matrix, K));
    }
}