[LeetCode] 1428. Leftmost Column with at Least a One

(This problem is an interactive problem.)

A binary matrix means that all elements are 0 or 1. For each individual row of the matrix, this row is sorted in non-decreasing order.

Given a row-sorted binary matrix binaryMatrix, return leftmost column index(0-indexed) with at least a 1 in it. If such index doesn't exist, return -1.

You can't access the Binary Matrix directly.  You may only access the matrix using a BinaryMatrix interface:

• BinaryMatrix.get(row, col) returns the element of the matrix at index (row, col) (0-indexed).
• BinaryMatrix.dimensions() returns a list of 2 elements [rows, cols], which means the matrix is rows * cols.

Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer.  Also, any solutions that attempt to circumvent the judge will result in disqualification.

For custom testing purposes you're given the binary matrix mat as input in the following four examples. You will not have access the binary matrix directly.

Constraints:

• rows == mat.length
• cols == mat[i].length
• 1 <= rows, cols <= 100
• mat[i][j] is either 0 or 1.
• mat[i] is sorted in a non-decreasing way.

至少有一个 1 的最左端列。

题目大意是给一个二维矩阵 matrix，里面只有 0 和 1 两种数字，matrix 的每一行的数字都是非递减的（但是每一列并不是非递减）。你不能直接访问这个 matrix，但是你可以通过给的接口访问 matrix 的一些东西，比如 dimensions() 可以拿到 matrix 的 dimension 尺寸，get(x, y) 可以拿到 某一个坐标上的值。请你返回这个矩阵里面最左边的包含起码一个 1 的 column 的 index。若这个 column 不存在则返回 -1。

• BinaryMatrix.get(row, col) returns the element of the matrix at index (row, col) (0-indexed).
• BinaryMatrix.dimensions() returns a list of 2 elements [rows, cols], which means the matrix is rows * cols.

几个例子如下，

Example 1:

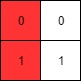
Input: mat = [[0,0],[1,1]]
Output: 0

Example 2:

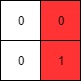
Input: mat = [[0,0],[0,1]]
Output: 1

Example 3:

Input: mat = [[0,0],[0,0]]
Output: -1

Example 4:

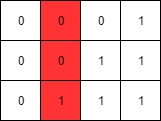
Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
Output: 1

我这里提供两种思路，一种是逐行扫描，一种是二分法。

首先是逐行扫描，先用 dimensions() 函数得到 matrix 的长和宽，然后从 matrix 的右下角的位置（m - 1, n - 1）开始看是否能找到一个 1。若 cur 为 0，则再往上一行找（i--）；若 cur 为 1，将当前坐标的纵坐标标记为 res，再往左边看是否还有纵坐标更小的 1。

时间O(m + n) - 长 + 宽

空间O(1)

Java实现

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * interface BinaryMatrix {
 *     public int get(int row, int col) {}
 *     public List<Integer> dimensions {}
 * };
 */

class Solution {
    public int leftMostColumnWithOne(BinaryMatrix binaryMatrix) {
        List<Integer> dimension = binaryMatrix.dimensions();
        int n = dimension.get(0);
        int m = dimension.get(1);
        int i = n - 1, j = m - 1, res = -1;
        while (i >= 0 && j >= 0) {
            int cur = binaryMatrix.get(i, j);
            if (cur == 0) {
                i--;
            } else {
                res = j;
                j--;
            }
        }
        return res;
    }
}

二分法的思路也比较直观。因为每一行是非递减的，所以是在对每一行做二分。我们一开始先试图对最后一行做二分，得到最后一行的 mid 坐标之后，我们看在最后一行的 mid 位置上是否存在 1，如果存在，则把 mid 暂时记录成 res，然后可以在 left - mid 的范围内再次对每一行扫描，看看是否在其他行存在一个 index 比 mid 更小的 1。

时间O(mlogn)

空间O(1)

Java实现

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * interface BinaryMatrix {
 *     public int get(int row, int col) {}
 *     public List<Integer> dimensions {}
 * };
 */

class Solution {
    public int leftMostColumnWithOne(BinaryMatrix binaryMatrix) {
        List<Integer> di = binaryMatrix.dimensions();
        int m = di.get(0);
        int n = di.get(1);
        int left = 0;
        int right = n - 1;
        int res = -1;
        while (left <= right) {
            // 某一行的中点mid
            int mid = left + (right - left) / 2;
            // 逐行扫描，看当前行是否在mid处是1
            if (helper(binaryMatrix, m, mid)) {
                res = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return res;
    }

    private boolean helper(BinaryMatrix binaryMatrix, int m, int c) {
        for (int r = 0; r < m; r++) {
            if (binaryMatrix.get(r, c) == 1) {
                return true;
            }
        }
        return false;
    }
}

LeetCode 题目总结