leetcode 99. 恢复二叉搜索树(dfs,遍历)

• 题目描述

给你二叉搜索树的根节点 root ，该树中的两个节点被错误地交换。请在不改变其结构的情况下，恢复这棵树。

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗？

 

示例 1：

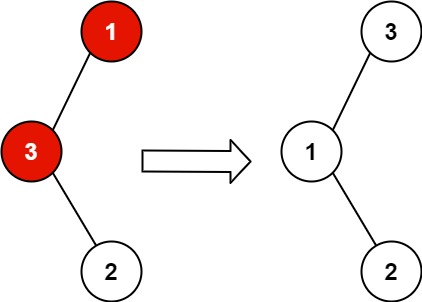
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2：

输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

• 解题思路—dfs+递归

二叉搜索树的中序遍历结果一定是一个从小到大递增的数组，那么我们则可以用中序遍历找到数组中这两个异常值点x，y。

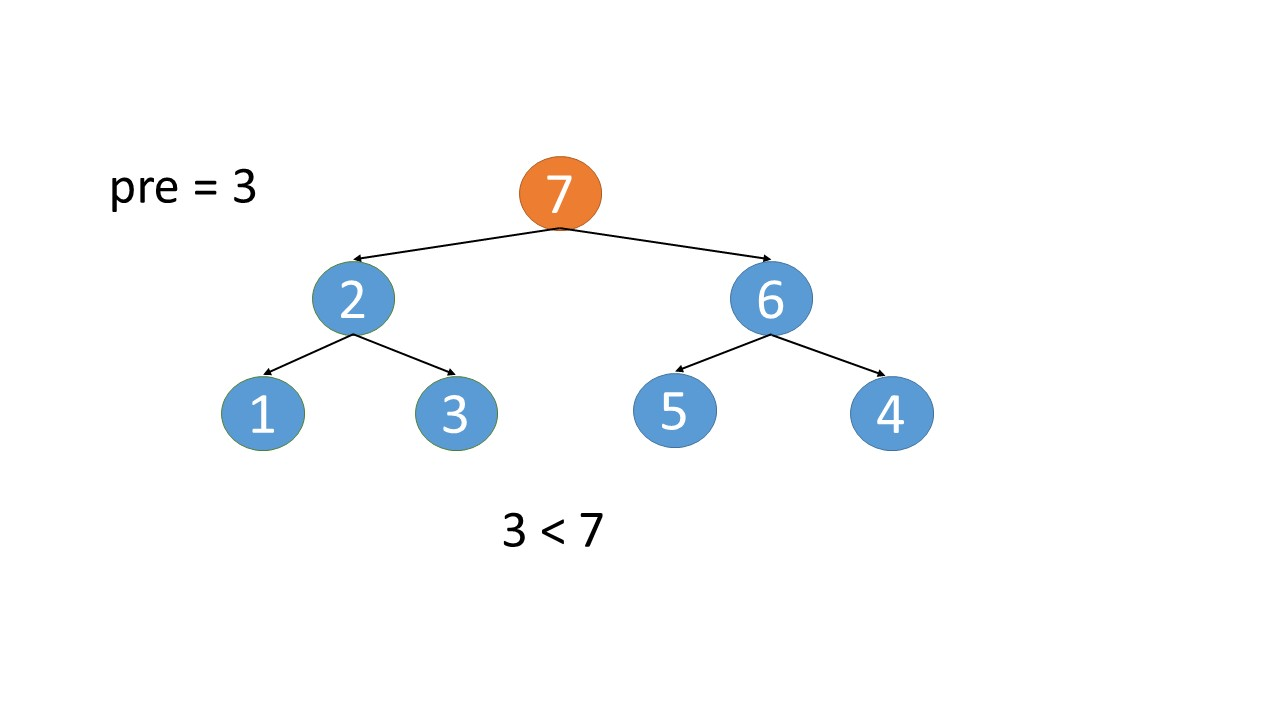
 对这颗二叉树中序遍历，我们用pre节点始终保存二叉树的根节点，然后判断上一个根节点是否大于下一个根节点，如果大于则保存为y节点，然后把上一个根节点保存为x节点。遍历完成后，如果x和y都不是空的话，说明这颗二叉搜索树存在乱序，进行交换即可。

这道题我觉得可以看下题解：https://leetcode-cn.com/problems/recover-binary-search-tree/solution/san-chong-jie-fa-xiang-xi-tu-jie-99-hui-fu-er-cha-/

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def recoverTree(self, root: TreeNode) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        self.x = None 
        self.y = None
        self.pre = None


        def dfs(root):
            if not root:
                return
            dfs(root.left)
            if not self.pre:
                self.pre = root
            else:
                if self.pre.val > root.val:
                    self.y = root
                    if not self.x:
                        self.x = self.pre 
                self.pre = root
            dfs(root.right)
        dfs(root)
        if self.x and self.y:
            self.x.val, self.y.val = self.y.val, self.x.val
        return root