• 堆与优先队列

    1.堆与优先队列

    普通的队列是一种先进先出的数据结构，即元素插入在队尾，而元素删除在队头。而在优先队列中，元素被赋予优先级，当插入元素时，同样是在队尾，但是会根据优先级进行位置调整，优先级越高，调整后的位置越靠近队头；同样的，删除元素也是根据优先级进行，优先级最高的元素（队头）最先被删除。另外，优先队列也叫堆。

    2.优先队列与二叉树

    首先，优先队列是二叉树的一种特例，是在二叉树的基础上，再定义一种性质：根节点的key值比左子树和右子树大（最大优先队列，也叫大顶堆）或小（最小优先队列，也叫小顶堆），通过在二叉树上维护这一性质，这样该二叉树就是优先队列。

    2.1 二叉树的性质

    在学习优先队列时，我们要先对二叉树有一定的认知。

    2.1.1 二叉树的定义

    二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

    2.1.2 二叉树的基本形态

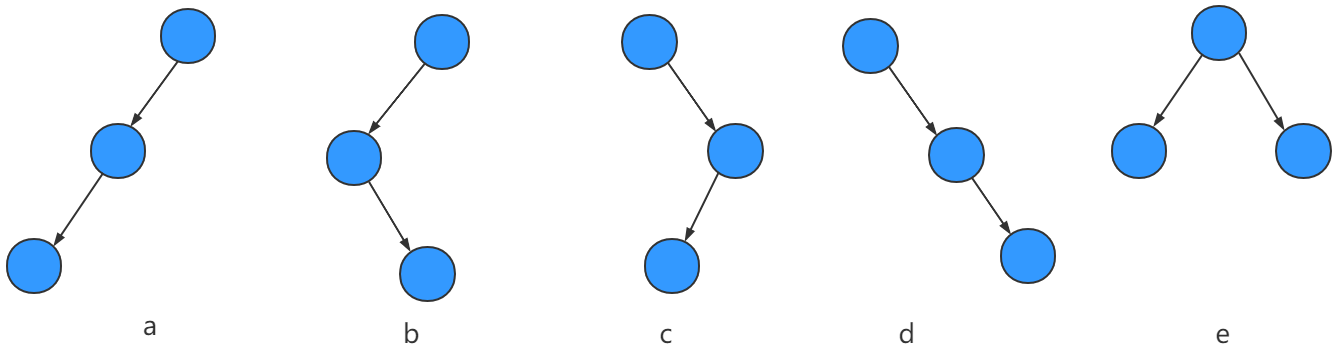
    二叉树是递归定义的，其结点有左右子树之分，逻辑上二叉树有五种基本形态： [3]
    1、空二叉树——如图（a）；
    2、只有一个根结点的二叉树——如图（b）；
    3、只有左子树——如图（c）；
    4、只有右子树——如图（d）；
    5、完全二叉树——如图（e）。

    由上述我们可以得知，一颗节点数为3的二叉树，有五种形态：
    image

    2.1.2 相关术语

    1、节点：至少包含一个key值得数据及若干指向子树分支的指针；
    2、节点的度：一个节点拥有的子节点的数目称为节点的度；
    3、叶子节点：度为0的节点；
    4、分支节点：度不为0的节点；
    5：数的度：数中所有节点的度的最大值；
    6、节点的层次：从根节点开始诉求你，假设根节点为第一层，根节点的子节点为第二层，一次类推，如果某一个节点位于第L层，则其子节点位于第L + 1层；
    7、树的深度：也称为树的高度，树种所有节点的层次最大值称为树的深度；

    2.1.3 二叉树的性质

    性质1：二叉树的第i层上至多有22-1(i >= 1)个节点；
    性质2：深度为h的二叉树中至多有2h - 1个节点；
    性质3：节点数为n的二叉树中，有n-1条边。
    性质4：若在任意一棵二叉树中，度为0的节点数目为n0，度为2的节点数目为n2，则n0 = n2 + 1.
    证明过程
    假设存在一棵节点数为n的二叉树，其中度为0的节点的数目为n0，度为1的节点的数目为n1，度为2的节点的数目为n2，求证n0 = n2 + 1。
    由于有n个节点，从性质3得到有n-1条边，其中n - 1 = n0 + n1 + 2n2，又因为n = n0 + n1 + n2，所以得到n0 + n1 + 2n2 + 1 = n0 + n1 + n2，化简得到 n0 = n2 + 1。

    2.1.4 特殊形式

    二叉树有两种特殊形式，分别为满二叉树和完全二叉树，如下图
    满二叉树（Full Binary Tree）
    一棵二叉树，如果每一层的节点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一棵二叉树的节点总数是2k - 1（k是二叉树层数），则它就是满二叉树。

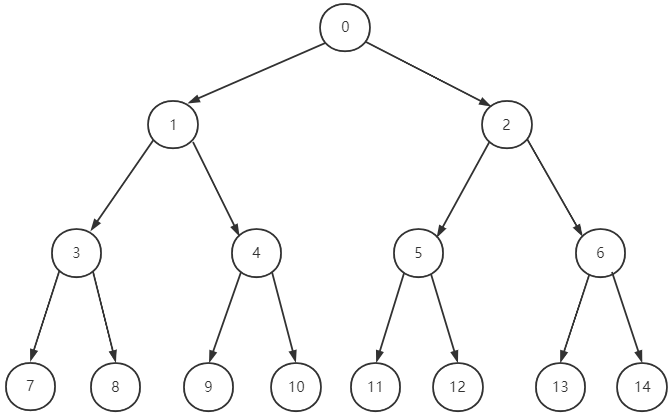
    我们可以得到结论：对于一棵k层的满二叉树而言，节点数一定是偶数，且为2k - 1，最后一层的节点数为2k-1。
    完全二叉树（Complete Binary Tree）
    完全二叉树：完全二叉树的节点数是任意的，从形式上讲它是个缺失的的三角形，但所缺失的部分一定是右下角某个连续的部分，也就是说最后那一层的节点数可能不是完整的。

    我们可以得到结论：对于一棵k层的满二叉树而言，节点数可以是偶数也可以是奇数，范围为：2k-1 <= n <= 2k - 1，最后一层的节点数为2k-1。
    其实，满二叉树是完全二叉树一种特例。
    完全二叉树的特殊性质
    性质：若对一棵有n个节点的完全二叉树进行顺序编号(1 <= i <= n)，那么，对于编号i（i >= 1）的节点：
    1）当i = 1时，该节点为根节点，且它没有父节点；
    2）当i > 1时，该节点的双清节点为i/2；
    3）若2i <= n，则有存在编号为2i的左孩子节点，否则则没有左孩子节点；
    4）若2i + 1 <= n，则存在编号为2i + 1的右孩子节点，否则则没有右孩子节点。
    这个性质非常重要，因为优先队列就是用完全二叉树去存储的。

    3 优先队列的储存方式

    由于优先队列本质上是二叉树的一种特殊例子，而二叉树的存储方式有两种：用链表实现或者用数组实现；这里，我们采用数组的形式去实现优先队列的存储方式，之所以能够用数组去实现优先队列的存储，就是由于上述完全二叉树的性质，具体看下图。


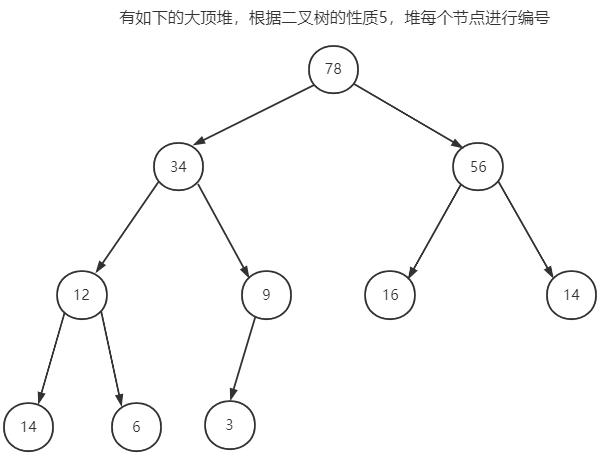
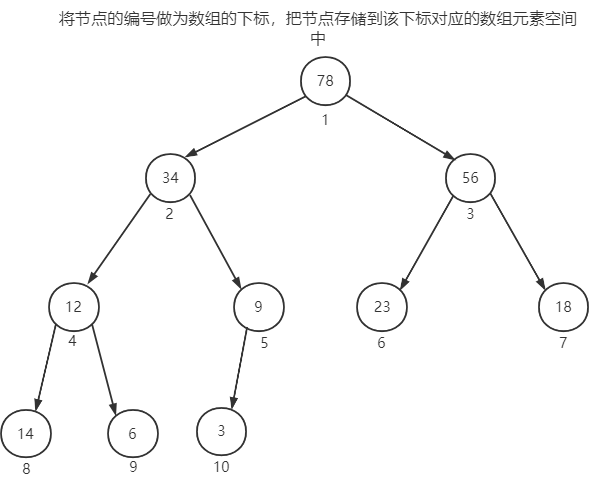
    这样，我们实现了用数组去存储优先队列，其中下标为0的节点不会存储元素，队头一直是下标1的元素，且队头是队列的最值，我们只需要在保证出队后，再次从队列中找到最值存放在队头，就可以保证下次出队的元素还是最值。

    4 优先队列的入队

    优先队列的插入跟普通的队列插入一样，都是在队尾插入，但是由于对于优先队列而言，每个节点的key值都比其左子树所有节点和右子树所有节点的key值大，所以我们需要在插入后，同样也要维护这一性质，所以我们还需要调整这个，如下图：
    插入节点
    以大顶堆为例，若新插入节点44，由于要保证优先队列的性质（某节点的key比左右节点的key大），所以我们需要调整44的位置。

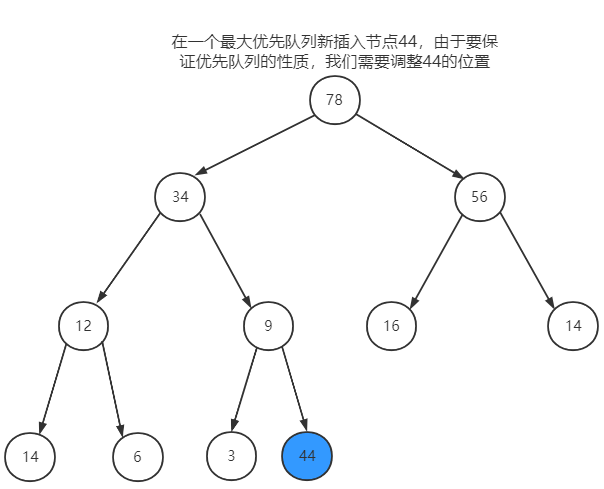
    根据完全二叉树的性质，我们从新插入的节点出发，一直向上对比父节点，比父节点的key大则与父节点交换位置，直到比父节点的key小为止，如下图：

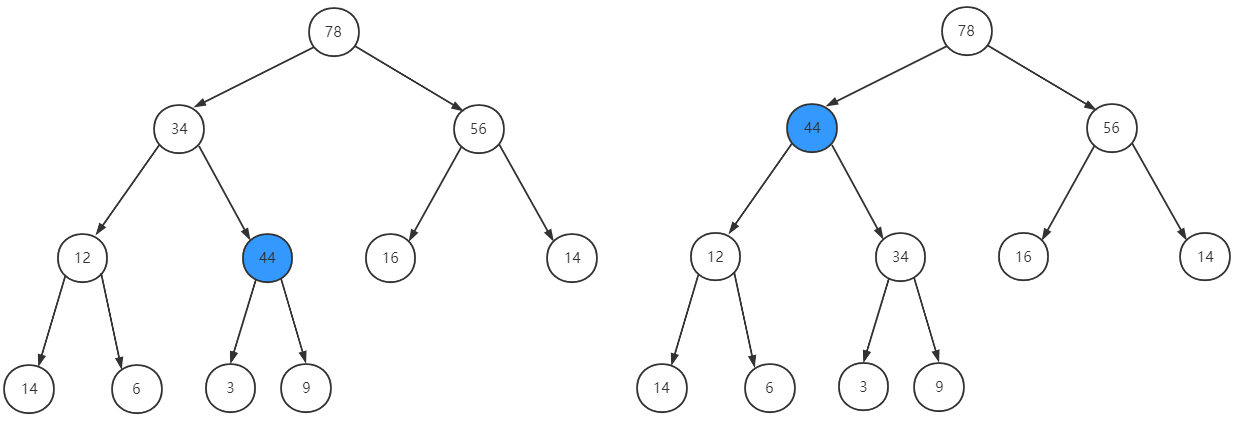
    5 优先队列的出队

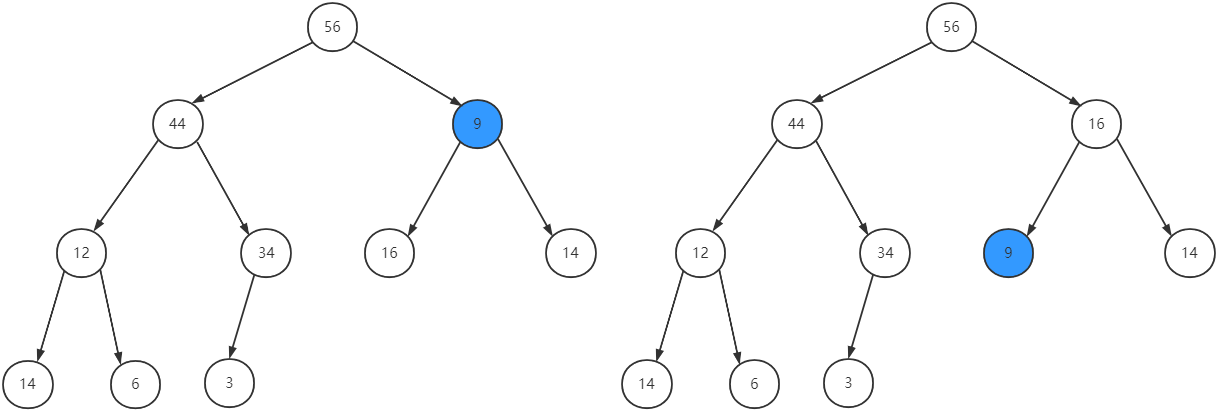
    优先队列出队后，队头元素的位置空出来了，这时候，我们要在队列里面找出最大值并将其移动到队头位置，一般的做法是先把队尾元素移动到队头，在调整这个队头元素的位置，以更新队头元素为最大值和维护优先队列的性质。
    出队

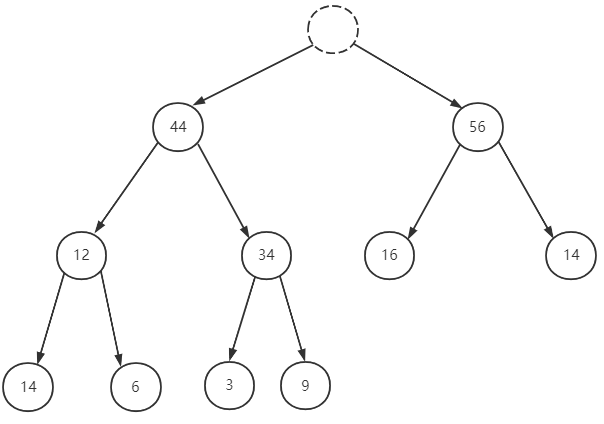
    移动队尾元素到队头位置

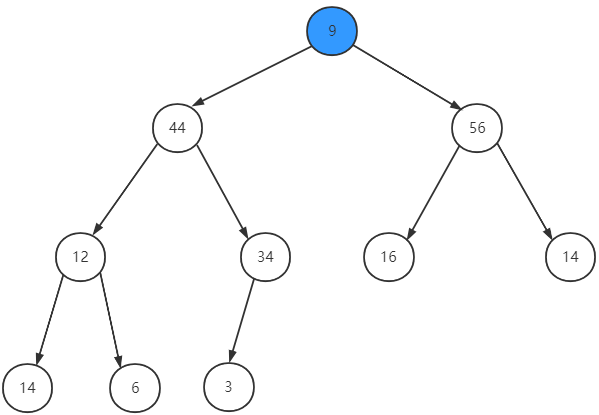
    调整位置以维护优先队列性质
    image

    6 代码实现

    6.1 结构定义

    typedef struct priority_queuie {
    int *data;
    int size, cnt;
} priority_queue;

    data：指向存储优先队列的数组指针；
    size：存储优先队列的数组容量；
    cnt：数组里存储的优先队列节点数。

    6.2 优先队列的初始化和销毁

    初始化

    priority_queue *init(int n) {
    priority_queue *q = (priority_queue *)malloc(sizeof(priority_queue));
    q->data = (int *)malloc(sizeof(int) * (n + 1));//多申请一个int，因为我们是从1开始存放数据
    q->cnt = 0;
    q->size = n;
    return q;
}

    销毁

    void clear(priority_queue *q) {
    if (q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}

    这两部分的代码都很简单，不解释。

    6.3 队列的判空和获取队首元素

    判空

    int empty(priority_queue *q) {
    return q->cnt == 0;
}

    获取队首元素

    int top(priority_queue *q) {
    return q->data[1];
}

    也很简单，不多做解释。

    6.4 入队操作

    int push(priority_queue *q, int val) {
    if (q == NULL) return 0;
    if (q->cnt == q->size) return 0;
    q->cnt++;
    q->data[q->cnt] = val;
    int index = q->cnt;
    while (index >> 1 && q->data[index] > q->data[index >> 1]) {//只要有父节点，且父节点比正在调整的节点的值大，则交换并更新调整节点的下标为父节点的下标
        swap(q->data[index], q->data[index >> 1]);
        index >>= 1;//更新当前节点的下标为父节点的下标
    }
    return 1;
}

    有完全二叉树的性质，我们可以得知一个结论，若某个非根节点的序号为index，无论它是其父节点的左孩子节点还是右孩子节点，其父节点的序号都为index/2，当前，这里的前提条件是优先队列的序号是从1开始。有了这个结论后，配合上面代码的注释，就可以很轻松看懂代码了。

    6.5 出队操作

    int pop(priority_queue *q) {
    if (q == NULL) return 0;
    if (empty(q)) return 0;
    q->data[1] = q->data[q->cnt];//把堆尾元素存放到堆顶
    q->cnt--;//总数减一表示删除掉一个元素，与上一行结合表示出堆
    int index = 1;//由于从堆顶删除了一个元素，所以必须在堆顶开始自上向下调节，以继续维护数组为堆
    while (index << 1 <= q->cnt) {//正在调节的节点有左孩子，则继续调节
        int temp = index, l = index << 1, r = index << 1 | 1;
        if (q->data[temp] < q->data[l]) temp = l;//左孩子的值比父节点大，则记录左孩子下标
        if (r <= q->cnt && q->data[temp] < q->data[r]) temp = r;//如果有右孩子，且右孩子的值比左孩子的值和父节点的值大，则temp记录右孩子的下标
        if (temp == index) break;//如果当前节点和左右孩子节点对比万，temp记录的还是当前节点的下标，则证明当前节点的值最大，从当前节点开始的子树是一个堆结构
        swap(q->data[temp], q->data[index]);//更新当前节点为值最大的孩子的值
        index = temp;//更新当前节点为值最大的孩子的下标
    }
    return 1;
}

    由上面入队提到的结论再加上出队代码里的注释，也可以看懂出队代码。

    6.6 总源码

    /*************************************************************************
        > File Name: priority_queue.c
        > Author: ydqun
        > Mail: qq2841015@163.com
        > Created Time: Sat 05 Dec 2020 07:50:58 PM CST
 ************************************************************************/

//堆有用到完全二叉树的性质去实现的，完全二叉树可以用数组去表示，这是因为可以根据父节点的下标去计算子节点。
//另外堆还定义了一个性质，父节点的值，左右节点的值三者之间，父节点的值最大。
//入堆操作为堆尾插入，并自下向上调整，使得继续维护堆顶元素最大的性质
//出堆则为把堆尾的元素和堆顶元素交换，然后再从堆顶元素开始自上向下调节，使得继续维护堆顶元素最大的性质

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define swap(a, b) {
    __typeof(a) _temp = a;
    a = b, b = _temp;
}

typedef struct priority_queuie {
    int *data;
    int size, cnt;
} priority_queue;

priority_queue *init(int n) {
    priority_queue *q = (priority_queue *)malloc(sizeof(priority_queue));
    q->data = (int *)malloc(sizeof(int) * (n + 1));//多申请一个int，因为我们是从1开始存放数据
    q->cnt = 0;
    q->size = n;
    return q;
}

void clear(priority_queue *q) {
    if (q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}

int empty(priority_queue *q) {
    return q->cnt == 0;
}

int top(priority_queue *q) {
    return q->data[1];
}

int push(priority_queue *q, int val) {
    if (q == NULL) return 0;
    if (q->cnt == q->size) return 0;
    q->cnt++;
    q->data[q->cnt] = val;
    int index = q->cnt;
    while (index >> 1 && q->data[index] > q->data[index >> 1]) {//只要有父节点，且父节点比正在调整的节点的值大，则交换并更新调整节点的下标为父节点的下标
        swap(q->data[index], q->data[index >> 1]);
        index >>= 1;//更新当前节点的下标为父节点的下标
    }
    return 1;
}

int pop(priority_queue *q) {
    if (q == NULL) return 0;
    if (empty(q)) return 0;
    q->data[1] = q->data[q->cnt];//把堆尾元素存放到堆顶
    q->cnt--;//总数减一表示删除掉一个元素，与上一行结合表示出堆
    int index = 1;//由于从堆顶删除了一个元素，所以必须在堆顶开始自上向下调节，以继续维护数组为堆
    while (index << 1 <= q->cnt) {//正在调节的节点有左孩子，则继续调节
        int temp = index, l = index << 1, r = index << 1 | 1;
        if (q->data[temp] < q->data[l]) temp = l;//左孩子的值比父节点大，则记录左孩子下标
        if (r <= q->cnt && q->data[temp] < q->data[r]) temp = r;//如果有右孩子，且右孩子的值比左孩子的值和父节点的值大，则temp记录右孩子的下标
        if (temp == index) break;//如果当前节点和左右孩子节点对比万，temp记录的还是当前节点的下标，则证明当前节点的值最大，从当前节点开始的子树是一个堆结构
        swap(q->data[temp], q->data[index]);//更新当前节点为值最大的孩子的值
        index = temp;//更新当前节点为值最大的孩子的下标
    }
    return 1;
}

int main(void) {
    #define max_op 20
    srand(time(0));
    priority_queue *q = init(max_op);
    for (int i = 0; i < max_op; i++) {
        int val = rand() % 100;
        push(q, val);
        printf("Insert %d to the priority queue
", val);
    }
    for (int i = 0; i < max_op; i++) {
        printf("%d ", top(q));
        pop(q);
    }
    printf("
");
    clear(q);
    #undef max_op
    return 0;
}

    对于整个程序，我们还编写了测试代码，其中有三种操作，分别为入队，出队和返回队首元素，我们先插入20个节点，节点的值为随机获取，接着我们分别进行获取队首元素和出队的操作20次，由于我们实现的是大顶堆，所以最终结果为输出一个降序的序列。
    编译并测试

    ydqun@VM-0-9-ubuntu priority_queue % gcc priority_queue.c                                                                                                                                   [1]
ydqun@VM-0-9-ubuntu priority_queue % ./a.out                                                                                                                                                   [0]
Insert 25 to the priority queue
Insert 41 to the priority queue
Insert 57 to the priority queue
Insert 81 to the priority queue
Insert 27 to the priority queue
Insert 54 to the priority queue
Insert 95 to the priority queue
Insert 32 to the priority queue
Insert 25 to the priority queue
Insert 2 to the priority queue
Insert 63 to the priority queue
Insert 60 to the priority queue
Insert 70 to the priority queue
Insert 38 to the priority queue
Insert 41 to the priority queue
Insert 87 to the priority queue
Insert 58 to the priority queue
Insert 5 to the priority queue
Insert 48 to the priority queue
Insert 79 to the priority queue
95 87 81 79 70 63 60 58 57 54 48 41 41 38 32 27 25 25 5 2

    7 结论

    对于优先队列，本质上它的实现是用完全二叉树来实现的，并且用到的存储模式是用数组，而非链表，这里是由于完全二叉树的性质决定了用数组来实现会非常容易。另外由最终的测试程序我们看到，对于大顶堆，每次输出队首元素并出队，连续操作到队列为空，输出的序列是一个降序序列，这里我们很容易联想到堆排序，没错，堆排序本质上也是用优先队列的思想去实现对一个无序数组有序化的，后面我也会在博客上编写有关堆排序理解的文章。
  • 相关阅读:
    二叉搜索树与双向链表
    TCP 三次握手与四次挥手
    复杂链表的复制
    二叉树中和为某一值的路径
    二叉搜索树的后序遍历序列
    从上往下打印二叉树
    栈的压入、弹出序列
    jenkins 持续集成和交付——一个构件小栗子前置(三)
    jenkins 持续集成和交付——gogs安装(外篇)
    jenkins 持续集成和交付——安装与账户安全还有凭证(二)
  • 原文地址：https://www.cnblogs.com/ydqblogs/p/14764781.html
Copyright © 2020-2023  润新知