机器学习算法题
线性回归和逻辑回归的异同? SVM和LR(逻辑回归)有什么不同?
线性回归的输入变量和输出变量都是连续的,逻辑回归的输入变量是连续的,输出变量是类别(或者说是离散的、枚举的)。
SVM和LR一般都用于处理分类问题,不同的是二者的实现原理,SVM是以支持向量到分类平面的距离最大化为优化目标,得到最优分类平面,LR是把输出类别以概率的方式表示,常用的是logistic sigmoid函数,然后通过极大似然或其他方法来构造最优化目标,进而求解得到最优参数。
[补充:有一个大厂的面试官提示我说,sigmoid是函数族,不是单个函数,用在LR里的是 Logistic Sigmoid函数。关于sigmoid函数族,我还没明白是什么意思。]
一阶和二阶正则化的区别是什么?分别适用于什么场合?
二者最大的区别在于是否可以把特征系数将为0,一阶惩罚项不仅可以降低模型复杂度,还可以同时完成特征筛选,即,把部分特征的系数降为0,二阶惩罚项可能会把部分特征的系数降到很小,但一般不会将特征的系数降为0。
适用的场合暂时还没有答案。
评价机器学习分类算法的指标有哪些?
常用的指标有:准确率(precision)、召回率(recall)、F值(F-score)、AUC(Area Under ROC Curve)。
分类问题根据预测值和真实值可以分为如下四类:
| 预测值 | |||
| Positive | Negative | ||
| 真实值 | Positive | TP | FN |
| Negative | FP | TN | |
解释:
TP:True Positive,模型预测是正例,并且预测正确;
FP:False Positive,模型预测是正例,但是预测错误;
TN:True Negative,模型预测是反例,并且预测正确;
FN:False Negative,模型预测是反例,但是预测错误。
TP FP TN FN 分别表示四个类别的测试样本数量,由这四个数值可以计算出:
Precision (P) = TP/(TP+FP)
解释:预测为正例的所有样本中,预测正确的占多大比例,归纳成一个字就是——“准”,因此也称为查准率。
Recall (R) = TP/(TP+FN)
解释:真实是正例的所有样本中,被预测出来的占多大比例,归纳成一个字就是——“全”,因此也称为查全率。
F = 2*P*R/(P+R)
解释:P和R的调和平均。
一般来说,P和R是不可兼得的,P越高R越低,反之亦然。如果我们想要同时获得尽量高的P和R,可以用F值作为评价指标。F值本质上是P和R的调和平均,如果对P和R有不同的倾向,可以在公式中加入权重。
此外,P-R曲线也可以用来评估模型性能。我们利用模型对所有测试样本打分,得分越高表示该样本是正例的概率越高,按照得分由大到小对测试样本排序,然后从头至尾,依次预测每个样本是正例,计算此时的P和R,便可以得到P-R曲线。
引用周志华老师的图:
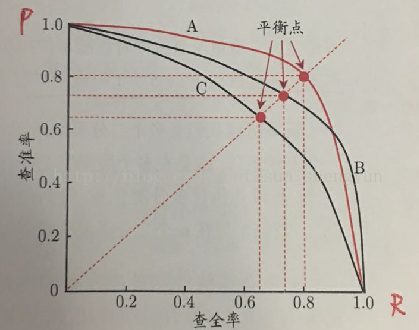
左上方的点,表示的是得分很高的测试样本的P和R,因为得分高,所以大多数是预测正确的,因此P很高,同时因为样本数量少,R很低,随着样本数量增加,R逐渐增加,P则逐渐减小,直到曲线走到右下角的位置,所有样本都被预测为正例,R一定是1,但是P很低。[补充:曲线的右下角不应该在 (0,1),应该在(p1,1)处,p1很小,这是个人的理解。]
什么是ROC曲线?横坐标和纵坐标分别是什么含义?曲线上的点是什么含义?
这是个非常重要的问题,面试中最起码被问过三次,因为这个指标是分类问题中最常用的评价指标。
ROC曲线和P-R曲线的构造思想比较相近,只是横纵坐标不同。同样是根据每个测试样本的得分(实值或概率值均可)按从大到小排序,然后从头至尾,逐个预测每个样本是正例,计算 TPR 和 FPR,再把TPR和FPR连接起来,就得到了ROC曲线。
TPR (True Positive Rate) = TP/(TP+FN) 解释:就是查全率。
FPR (False Positive Rate) = FP/(FP+TN) 解释:和查全率类似,把反例当做正例,相当于反例的查全率。
再次引用周老师的图:
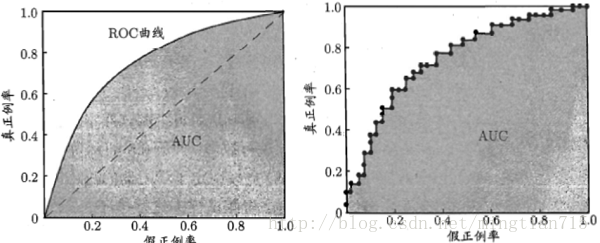
左图是理想的ROC曲线,右图是实际应用时得到的ROC曲线。曲线从左下角开始,这时测试样本数量很少,因此TPR和FPR都很小,随着样本数量增加,二者同步增加。更加的理想的情况是,TPR增加的快,FPR增加的慢,即,模型找到的正例更多,反例更少,这就对应了图中更靠上方的点,理解了这一点有助于理解AUC。样本全部判定为正例时,达到了ROC的右上角位置,此时所有正例和所有反例都被找出来了,所以TPR和FPR都是1.0。
ROC曲线和P-R曲线一样,如果模型A的ROC曲线能包裹住模型B的ROC曲线,说明模型A更优。如果模型A和模型B的ROC曲线有交叉,仍要对比二者,就可以用AUC,即ROC曲线下方的面积。AUC越大,模型越好。
[个人见解] 如果两个模型的ROC曲线有交叉,那么它们的AUC可能差距不大,比如一个是0.900,一个是0.901,此时硬说AUC略大的模型更优并没有太大意义。
ROC曲线有明确的起点和终点,分别是(0,0)和(1,1),所以AUC最大只能是1,最小是0,连接起点和终点的直线是AUC为0.5的分界线,这条线表示测试样本中正例和反例成对出现,相当于随机猜测。只要模型比随机猜测更好,AUC就应该大于0.5。
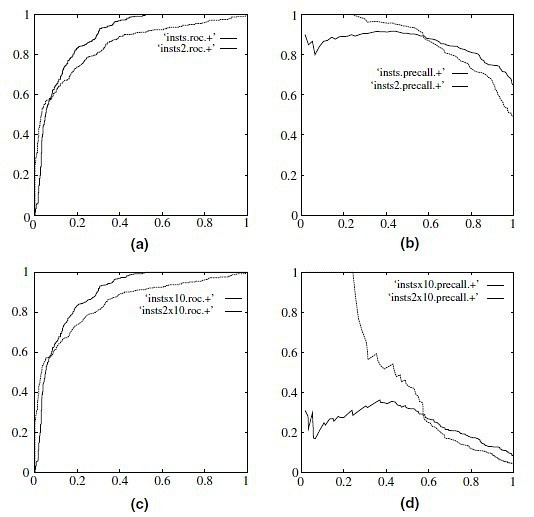
ROC曲线和P-R曲线是什么关系? 参考 豆瓣文章,P-R曲线和ROC曲线本质上是一一对应的关系,相对来看,P-R曲线比ROC曲线更能反应出模型的性能,这是因为样本存在类别不平衡问题。我们设想一下,如果样本中的正例特别少,反例特别多,对ROC曲线的主要影响是,TPR很可能早早就达到了1,使得ROC曲线的右半部分的纵坐标都是1.0,形如下图的(a)和(c)中颜色较深的曲线,对P-R曲线的影响很大,正例非常少,可能导致P一直很低或快速降低(因为预测正确并不容易),R则较快的到达接近1的位置,类似图(d)中的两条曲线的样子,这时,使用P-R曲线更能明显的反应出不同的模型的性能。 有一篇参考文献可以阅读: The Relationship Between Precision-Recall and ROC Curves ,尚未阅读,先在这留个名。
[关于两条曲线关系的理解还很浅,缺少更深入的调研和实践,先写在这里,供日后被拍砖。]
如何做特征筛选?
这个问题是机器学习的老生常谈,在机器学习领域,有一个说法是:特征选取决定了机器学习效果的上届,模型只是在逼近这个上界。这个说法似乎只是为了强调特征的重要性,并没什么实践上的指导意义,可以把它当做理论家的又一句经典的废话。
做特征筛选的主要原因是特征过多,这是实际问题中时常遇到的情况,特征太多会导致机器学习耗时太长,所以需要删除一些没用的特征。
具体的做法可以分为三种,过滤式、包裹式和嵌入式,原汁原味的书面表达可以参考周志华老师的《机器学习》248页。这里简单说说我的理解。
假如一个实际问题给到你,有1000个特征,要做特征筛选,你会怎么做?
最暴力的方法是选取每一个子集,评估模型的预测或分类效果,选择最优的子集。很显然,时间复杂度太高,不可行。既然不能暴力搜索,就退而求其次,改成随机搜索,这就是包裹式特征筛选方法。
包裹式方法的一个明显的缺点是时间开销很大,虽然不是暴力搜索,但是每次评估都要进行模型训练、测试和评估,时间开销依然不小。所以,另外一个特征筛选的思路是不去管模型,只是给每个特征打分,把得分高的特征留下,得分低的特征去除,这就是过滤式,经典的打分方法是Relief,这个算法比较好理解,详细算法可以参考周老师的书或这篇文章。
嵌入式特征筛选是指模型本身自带特征筛选能力,比如带L1正则化的模型(如Lasso)。
[注意:1. 这里的特征筛选都是在有监督学习场景下的,似乎不适用于无监督聚类;2. 有些模型不需要做特征筛选,比如 随机森林。]
如果机器学习的分类或预测效果不佳,如何改善?
这是个开放问题,可以边工作边补充,目前想到的答案有:
(1)选择更多的特征 (2)获取更多的训练和测试数据 (3)使用不同的模型 (4)检查数据是否有错误
模型复杂度和泛化能力之间的关系是怎样的?
关于泛化能力的描述,周志华老师和李航老师有两个不同的视角。
先看李航老师的。
模型复杂度与误差之间的关系如下:

这两条曲线比较好理解,模型复杂度越高,拟合出的曲线和训练样本越接近,误差自然越小,然而恰恰因为过度拟合了样本内数据,导致样本外数据的测试误差反而变大。
所以,训练误差会随模型复杂度的提高而单调下降,但是测试误差与模型复杂度有U型关系。这里,测试误差可以理解为模型的泛化能力,也就是说,泛化能力与模型复杂度之间是U型关系。
再来看周志华老师的。

泛化能力可以分解为三部分:偏差 + 方差 + 噪声。
两张图最大的不同点是下面的图多了一条线:方差曲线。这里的方差不是指样本本身的方差,是指样本发生变化时,模型变化的程度有多大。
另外,下图的横坐标是“训练程度”,上图的横坐标是“模型复杂度”,周志华老师提到的“训练程度”是否包括模型复杂度以外的成分,有待进一步思考。
第三个不同点是,上图的“测试误差”对应了下图的“泛化误差”,我暂时认为这两个概念是金丝相同的。
某大厂面试官提到了一个问题:随着样本数量增加,训练误差和测试误差如何变化? 我和小伙伴们讨论了一通,得到下面的答案:
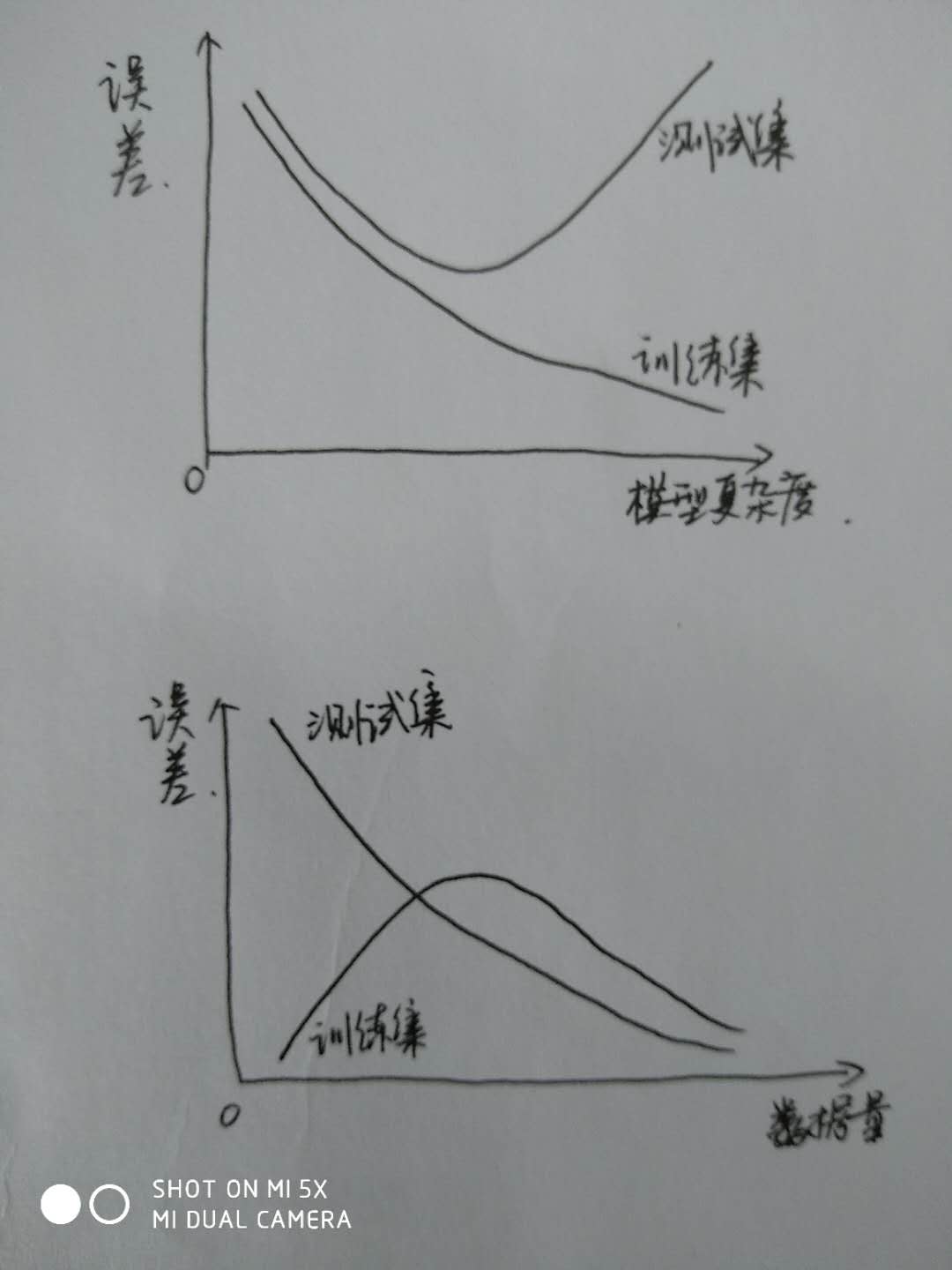
简单解释一下第二张图,用极限法,训练样本只有一、两个时,模型很容易覆盖所有训练数据,所以训练误差很小,同时,由于训练数据太少,模型很难从训练数据中提取数据的内在规律,所以测试误差很高,随着数据量增加,训练集的误差会先增加,等到训练集包含了足够多的信息后,训练误差会开始逐渐下降,由于模型对数据规律的拟合效果是越来越好的,所以测试误差会越来越小。
bagging和boosting的原理?
bagging(装袋法)和 boosting(提升法)都是ensemble learning(集成学习)的实现方法。
先说 ensemble。ensemble learning 的核心思想是把若干个弱学习器组合成一个强学习器,那么,为什么弱学习器组合起来就会变强呢?首先,这个结论是经过事实验证的,我们需要认可这个事实。其中的原因有点像概率统计中的大数定理,不同点在于,大数定理中的实验是独立且重复的,但是集成学习中的弱学习器不能是相同的,而应当是好而不同的。这里的“好”是个模糊的概念,可以理解为不坏。用学生来比喻集成学习就是:把若干个考试70、80分的学生组成一个团队,共同答题,就能得99甚至100分。
bagging 在构建弱学习器时,采用有放回的采样,英文里叫 bootstrap方法,每次从train set中做有放回的随机采样,训练得到弱学习器,重复这一过程,得到若干个弱学习器,然后把这些弱学习器组合起来,构成强学习器,用于判定或预测。最常用的bagging类型算法是RandomForest(随机森林)。
PS:对随机采样有个理解错误,bootstrap是有放回的采样,也就是说,每次抽出的样本集里可能包含train set中的重复数据,比如,train set是(1,2,3,4),有放回随机抽样的结果可能是(1,1,2,3)。
boosting 是采用逐步增强的方式构建强学习器,首先训练出一个弱学习器,然后根据弱学习器的训练误差,再训练出一个弱学习器,把两个弱学习器组合起来(通常是加法),得到增强的学习器,可以得到更小的训练误差,重复上述过程,直到达到迭代次数的上限或误差足够小。常见的boosting算法是AdaBoost和GBDT(含增强版的XGBoost)。
为了便于记忆,可以简单理解为:bagging 是学习器并联,boosting 是学习器串联。
[注意:我们上述提到的弱学习器都是同质的,比如都是决策树,这也是最常用的方法。弱学习器不同质时如何处理,有待进一步学习。]
参考文献:
https://blog.csdn.net/qq_36330643/article/details/77621232
=======未完待续===========
K-means和DBSCAN有什么异同?
如何确定K-means算法中的K值?
不同的特征是否需要都要做归一化?
高斯核函数和多项式核函数分别适用于什么情况?
EM算法的理解?
GBDT算法的理解?
如何用遗传算法生成技术指标?
相关系数的定义?