【填坑】可持久化线段树主席树 （两道模板题）

要解决的问题：

给定一个数列，每次查询任意区间的第k小数

基本方案：

例如数列 1 3 2 3 6 1

对于每个1~i  (1<=i<=n) 区间均建立一棵权值线段树，记录这个区间中每种数字的个数

1~4区间的线段树如下

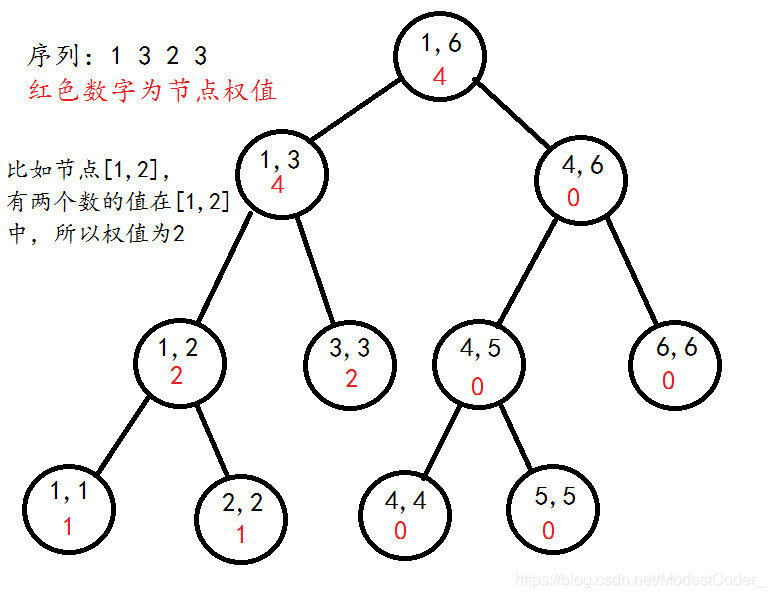
 对于每个节点，权值均为区间1~4的数在节点代表的区间中出现的次数。

按此方法构造n棵线段树，由前缀和思想可知，我们可以用两棵树相减来得出给定区间的权值线段树

若想求x~y区间的权值线段树，用1~y的树减去1~x-1的树即可 (x<y)

必要的空间优化：

构造n棵线段树太过浪费空间，事实上，在我们按顺序构造线段树时，有许多点的权值没有变化，是可以重复利用的

如下图：

序列为 4 3 2 3 6 1

 

 

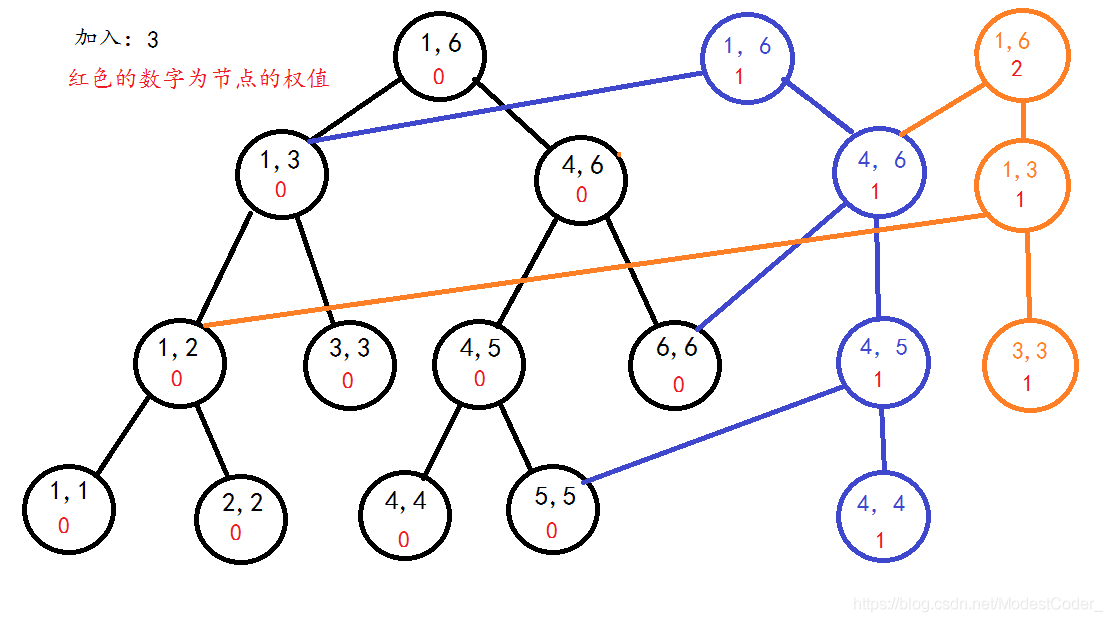
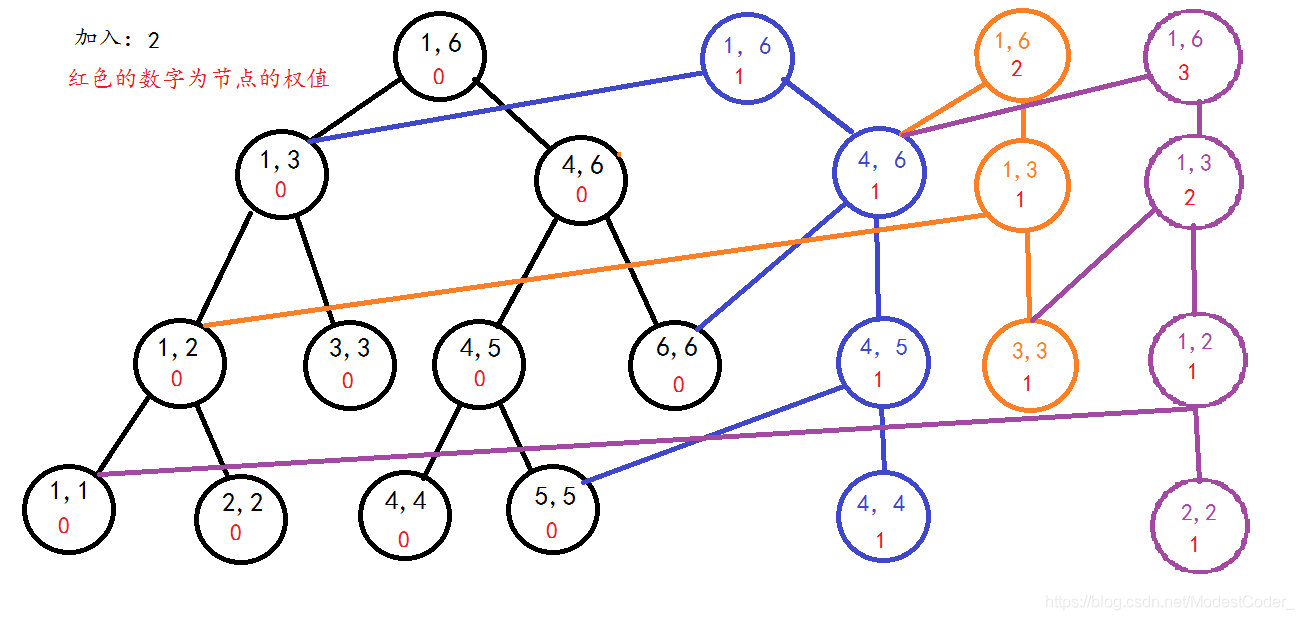
 节约了很多空间

具体实现：

• a、b数组，储存输入数据
• sz：节点个数
• rt数组：存储每棵线段树的根节点编号
• lc、rc数组：记录左儿子、右儿子编号，类似于动态开点
• sum数组：记录节点权值
• p：记录离散化后序列长度，也是线段树的区间最大长度

首先预处理，数列中的数可能不是连续的，离散化处理可以节约空间，q即为建立的树的叶子节点的数量

for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];//复制a数组
sort(b + 1, b + 1 + n);
q = unique(b + 1, b + 1 + n) - b - 1;//unique函数，返回值为去重后的序列长度

然后建立一棵点权均为0的空树

void build(int &rt, int l, int r)
{
    rt = ++sz, sum[rt] = 0;//新点
    if (l == r) return;//叶子结点，退出
    int mid = (l + r) >> 1;//mid
    build(lc[rt], l, mid); build(rc[rt], mid + 1, r);//往下走
}


build(rt[0], 1, q);//空树看成第0棵树

按1~n的顺序，把每个新点都当作根节点来建树

for (int i = 1; i <= n; ++i)
{
    p = lower_bound(b + 1, b + 1 + q, a[i]) - b;//找出新加入的点的位置，用lower_bound
    rt[i] = update(rt[i - 1], 1, q);
} 

这是建树用的update函数，用二分思想把新点所在区间的权值加一（所有子区间都要更新，每个需要更新的区间都要建立一个新的节点）

int update(int o, int l, int r)
{
    int oo = ++sz;//新点
    lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;//继承原点的信息，权值+1
    if (l == r) return oo;//叶子结点，退出
    int mid = (l + r) >> 1;//mid
    if (mid >= p) lc[oo] = update(lc[oo], l, mid); else rc[oo] = update(rc[oo], mid + 1, r);//新加入的节点在哪个区间，就走到哪个区间里去
    return oo;//返回值为新点编号
}

查询操作，b数组中储存的是去重后的数列

while (m--)
{
        int l = read(), r = read(), k = read();
        printf("%d
", b[query(rt[l - 1], rt[r], 1, q, k)]);//前缀和思想，[1,r]-[1,l-1]=[l,r]
}

query函数，返回值为目标数在b数组中的位置

int query(int u, int v, int l, int r, int k)
{//u、v为两棵线段树当前节点编号，相减就是询问区间
    int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];//sum相减，前缀和思想，看在左侧区间有多少个数
                                                        //然后与k比较(因为已经排过序了)
    if (l == r) return l;//叶子结点，找到kth目标，退出
    if (x >= k) return query(lc[u], lc[v], l, mid, k); else return query(rc[u], rc[v], mid + 1, r, k - x);
    //kth操作，排名<=左儿子的数的个数，说明在左儿子，进入左儿子；反之，目标在右儿子，排名需要减去左儿子的权值
}

注意，主席树一般开32倍空间

例题：

洛谷P3834

完整模板

#include <bits/stdc++.h>
#define maxn 200010
using namespace std;
int a[maxn], b[maxn], n, m, q, p, sz;
int lc[maxn << 5], rc[maxn << 5], sum[maxn << 5], rt[maxn << 5];
//空间要注意

inline int read(){
    int s = 0, w = 1;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;
    for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);
    return s * w;
}

void build(int &rt, int l, int r){
    rt = ++sz, sum[rt] = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(lc[rt], l, mid); build(rc[rt], mid + 1, r);
}

int update(int o, int l, int r){
    int oo = ++sz;
    lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;
    if (l == r) return oo;
    int mid = (l + r) >> 1;
    if (mid >= p) lc[oo] = update(lc[oo], l, mid); else rc[oo] = update(rc[oo], mid + 1, r);
    return oo;
}

int query(int u, int v, int l, int r, int k){
    int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];
    if (l == r) return l;
    if (x >= k) return query(lc[u], lc[v], l, mid, k); else return query(rc[u], rc[v], mid + 1, r, k - x);
}

int main(){
    n = read(), m = read();
    for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];
    sort(b + 1, b + 1 + n);
    q = unique(b + 1, b + 1 + n) - b - 1;
    build(rt[0], 1, q);
    for (int i = 1; i <= n; ++i){
        p = lower_bound(b + 1, b + 1 + q, a[i]) - b;
        rt[i] = update(rt[i - 1], 1, q);
    } 
    while (m--){
        int l = read(), r = read(), k = read();
        printf("%d
", b[query(rt[l - 1], rt[r], 1, q, k)]);
    }
    return 0;
}

例二

hdu6601 

解必定是相邻的三个数，对每个区间依次查询第1大第2大第3大，不成立则查询第2大第3大第4大，以此类推

#include <bits/stdc++.h>
#define maxn 200010
using namespace std;
int a[maxn], b[maxn], n, m, q, p, sz;
int lc[maxn << 5], rc[maxn << 5], sum[maxn << 5], rt[maxn << 5];
//空间要注意

inline int read(){
    int s = 0, w = 1;
    char c = getchar();
    for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;
    for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);
    return s * w;
}

void build(int &rt, int l, int r){
    rt = ++sz, sum[rt] = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(lc[rt], l, mid); build(rc[rt], mid + 1, r);
}

int update(int o, int l, int r){
    int oo = ++sz;
    lc[oo] = lc[o], rc[oo] = rc[o], sum[oo] = sum[o] + 1;
    if (l == r) return oo;
    int mid = (l + r) >> 1;
    if (mid >= p) lc[oo] = update(lc[oo], l, mid); else rc[oo] = update(rc[oo], mid + 1, r);
    return oo;
}

int query(int u, int v, int l, int r, int k){
    int mid = (l + r) >> 1, x = sum[lc[v]] - sum[lc[u]];
    if (l == r) return l;
    if (x >= k) return query(lc[u], lc[v], l, mid, k); else return query(rc[u], rc[v], mid + 1, r, k - x);
}

int main(){
    while(~scanf("%d%d",&n,&m))
    {
        for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i];
        sort(b + 1, b + 1 + n);
        q = unique(b + 1, b + 1 + n) - b - 1;
        build(rt[0], 1, q);
        for (int i = 1; i <= n; ++i)
        {
            p = lower_bound(b + 1, b + 1 + q, a[i]) - b;
            rt[i] = update(rt[i - 1], 1, q);
        }
        while (m--)
        {
            int l = read(), r = read();
            int len=r-l+1;
            long long ans=-1;
            while(len>=3)
            {
                long long x1,x2,x3;
                x1=b[query(rt[l-1],rt[r],1,q,len)];
                x2=b[query(rt[l-1],rt[r],1,q,len-1)];
                x3=b[query(rt[l-1],rt[r],1,q,len-2)];
                if(x1<x2+x3)
                {
                    ans=1LL*x1+1LL*x2+1LL*x3;
                    break;
                }
                len--;
            }
            printf("%lld
",ans);
        }
    }
    return 0;
}