抓老鼠
某地老鼠成灾,现悬赏抓老鼠,每抓到一只奖励10元,于是开始跟老鼠斗智斗勇:每天在墙角可选择以下三个操作:放置一个带有一块奶酪的捕鼠夹(T),或者放置一块奶酪(C),或者什么也不放(X)。捕鼠夹可重复利用,不计成本,奶酪每块3元。
聪明的老鼠呢?它们每天可能会派出一只老鼠到墙角,看看墙角有啥:
若什么也没有(X),老鼠们就不高兴了(Unhappy),会有长达一天(也就是第二天)的不高兴期。在不高兴期间,不派出老鼠。不高兴期结束之后,派出老鼠。
若有捕鼠夹(T),这只老鼠被引诱吃掉奶酪并被打死(Dead),老鼠们会有长达两天(也就是第二和第三天)的伤心期。在伤心期间,不派出老鼠。伤心期结束之后,派出老鼠。在这种情况下,抓到1只老鼠可获得奖励10元,但同时也耗费了一块奶酪。注意,如果某一天放置了捕鼠夹但老鼠没有出现,则没有耗费奶酪。
若有奶酪(C),老鼠吃了奶酪会很开心(Happy!),会有长达两天(第二和第三天)的兴奋期。在兴奋期间,即使叠加了不高兴或者伤心,也必定派出老鼠。在这种情况下,没抓到老鼠,而且耗费了一块奶酪。注意,如果某一天放置了奶酪但老鼠没有出现,则奶酪可以下次再用,没有耗费。
现在给你连续几天的操作序列,且已知第一天肯定会派出老鼠,请判断老鼠每天的状态,并计算盈利。
输入格式:
输入在一行中给出连续的由C或T或X组成的不超过70个字符的字符串,以$结束。字符串中每个字符表示这一天的操作( 即X:什么都不放;T:放捕鼠夹;C:放奶酪)。题目保证至少有一天的操作输入。
输出格式:
要求在第一行输出连续的字符串,与输入相对应,给出老鼠的状态:
! 表示派出老鼠吃到奶酪
D 表示派出老鼠被打死
U 表示派出老鼠无所获
- 表示没有派出老鼠
第二行则应输出一个整数表示盈利。(如果有亏损,则是负数)
输入样例1:
TXXXXC$
输出样例1:
D--U-!
4
输入样例2:
CTTCCX$
输出样例2:
!DD--U
11
流程图
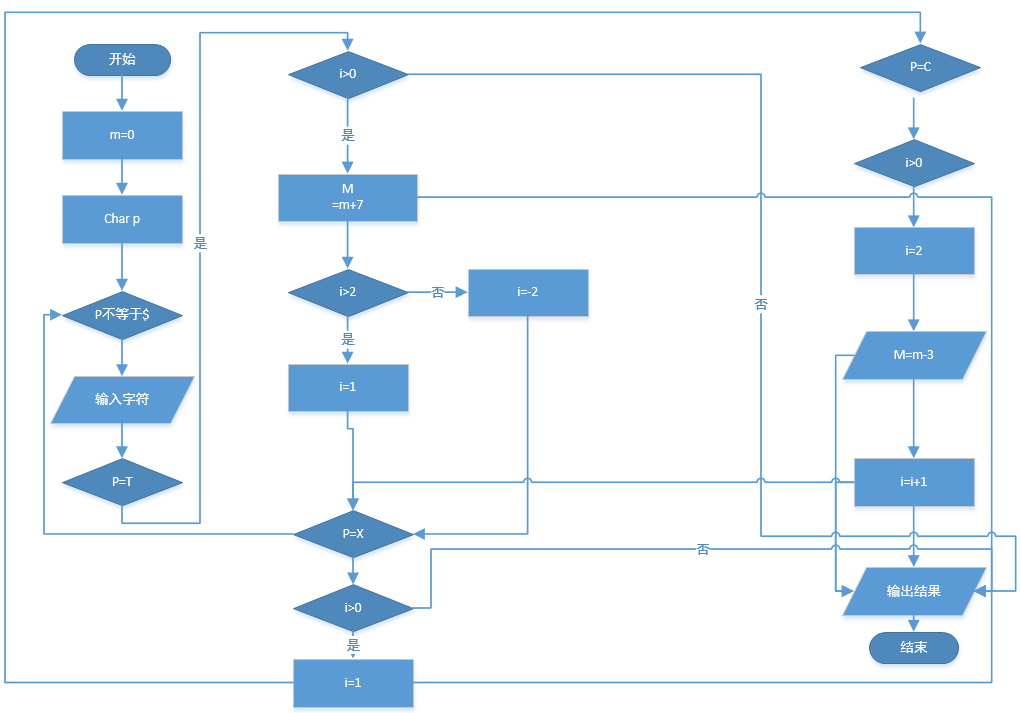
实验代码
#include<stdio.h>
int main()
{
int m=0,i=1;
char p; /*定义字符变量*/
while(p!='$') /*判断字符,成立则进入循环*/
{
scanf("%c",&p);
if(p=='T')
{
if(i>0)
{
m=m+7; /*依题意*/
printf("D");
if(i>2)
{
i=1;
}
else
{
i=-2;
}
}
else
{
printf("-");
}
}
if(p=='X')
{
if(i>0)
{
i=-1;
printf("U");
}
else
{
printf("-");
}
}
if(p=='C')
{
if(i>0)
{
i=2;
m=m-3;
printf("!");
}
}
i++;
}
printf("
%d",m);
return 0;
}
实验步骤
首先定义字符变量,整型变量。根据题意,可以先判断输入的数据,符合则可进入循环,利用嵌套式循环,m代表所花钱,可以分成三种情况,每成立一种情况可以计算所花钱,最后算出总花费,再做比较,最后看看是否亏了。