前言
一、方法总结
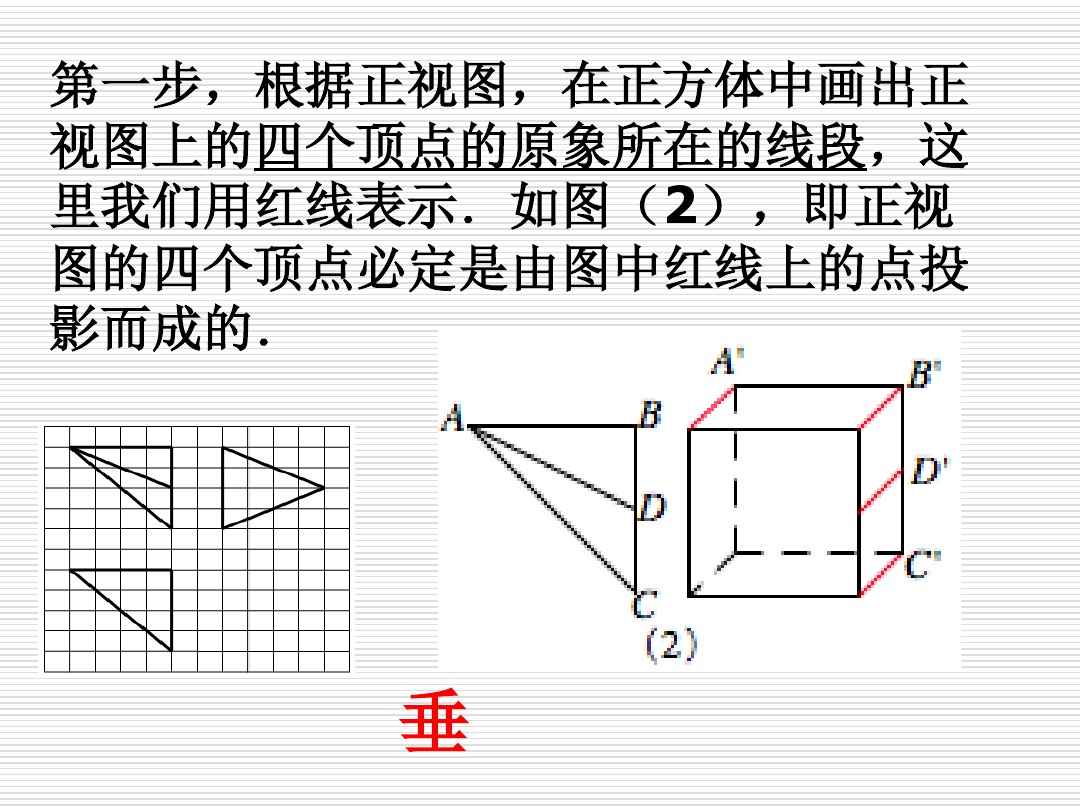
- 三视图还原为直观图的方法


二、典例剖析
一个几何体的三视图如图所示,则该几何体的体积为_____________。

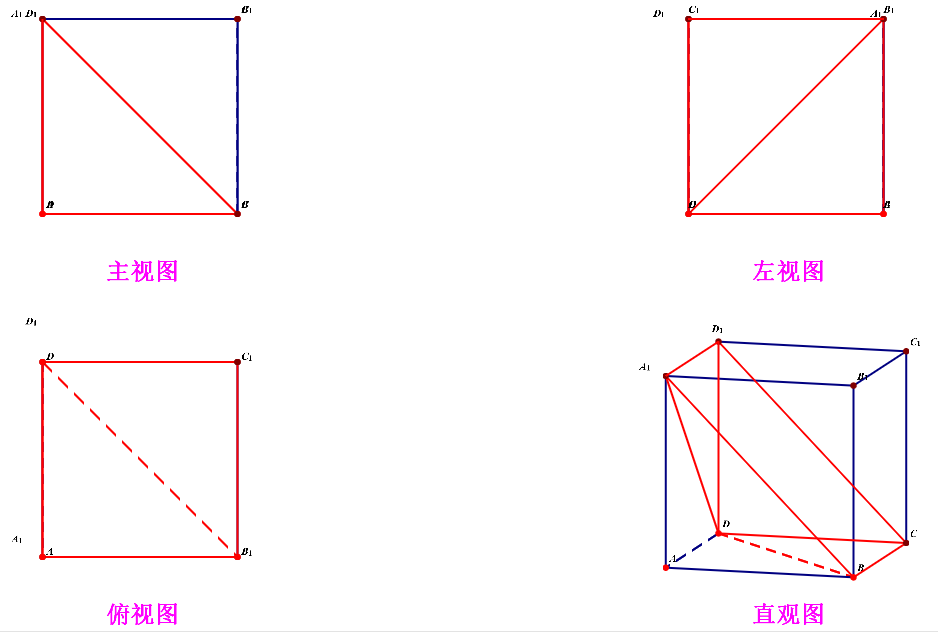
分析:由题目给定的三视图我们可以看出,原几何体的长、宽、高都是2,故我们先做一个正方体的模型备用,暂时不用标记顶点字母。
然后观察正视图中的所有顶点,将其顶点所落的正方体中的线段用红色标记并加粗,如下图所示;
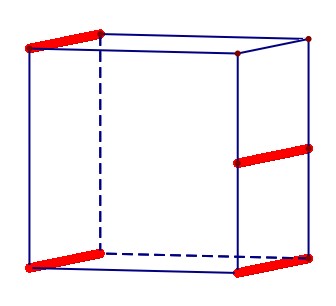
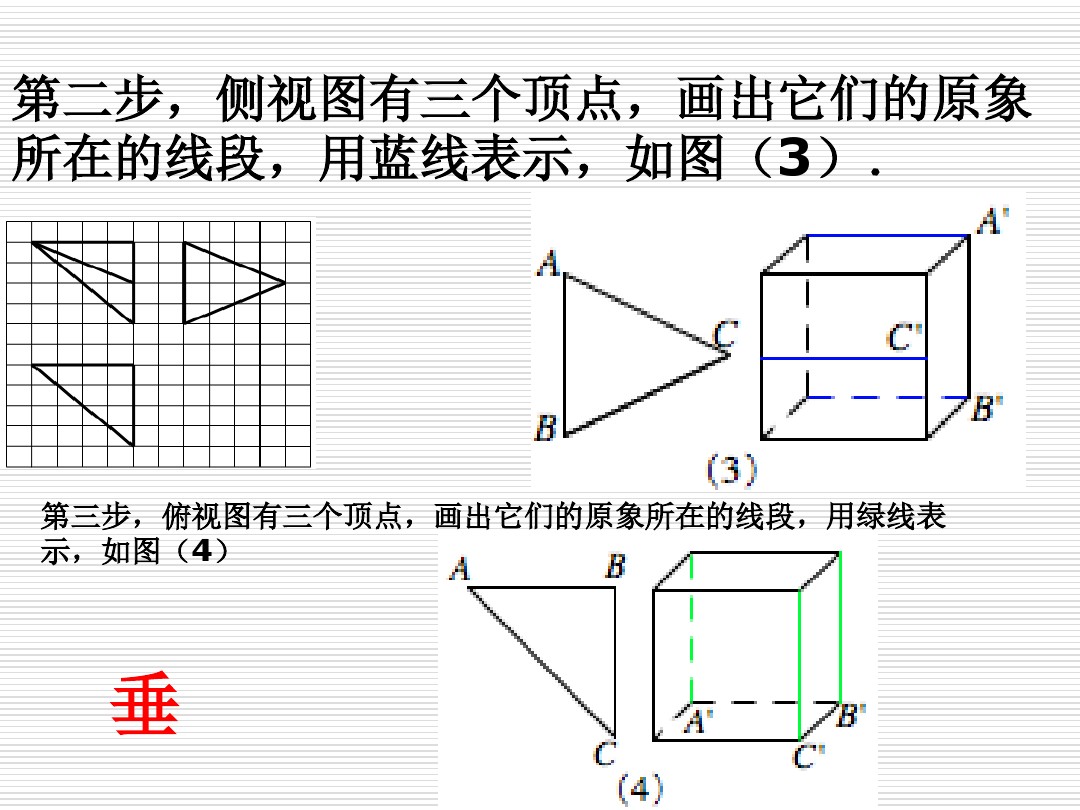
然后观察左视图中的所有顶点,将其顶点所落的正方体中的线段用蓝色标记并加粗,如下图所示;

再观察附视图中的所有顶点,将其顶点所落的正方体中的线段用绿色标记并加粗,如下图所示;
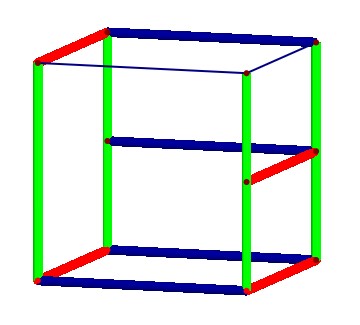
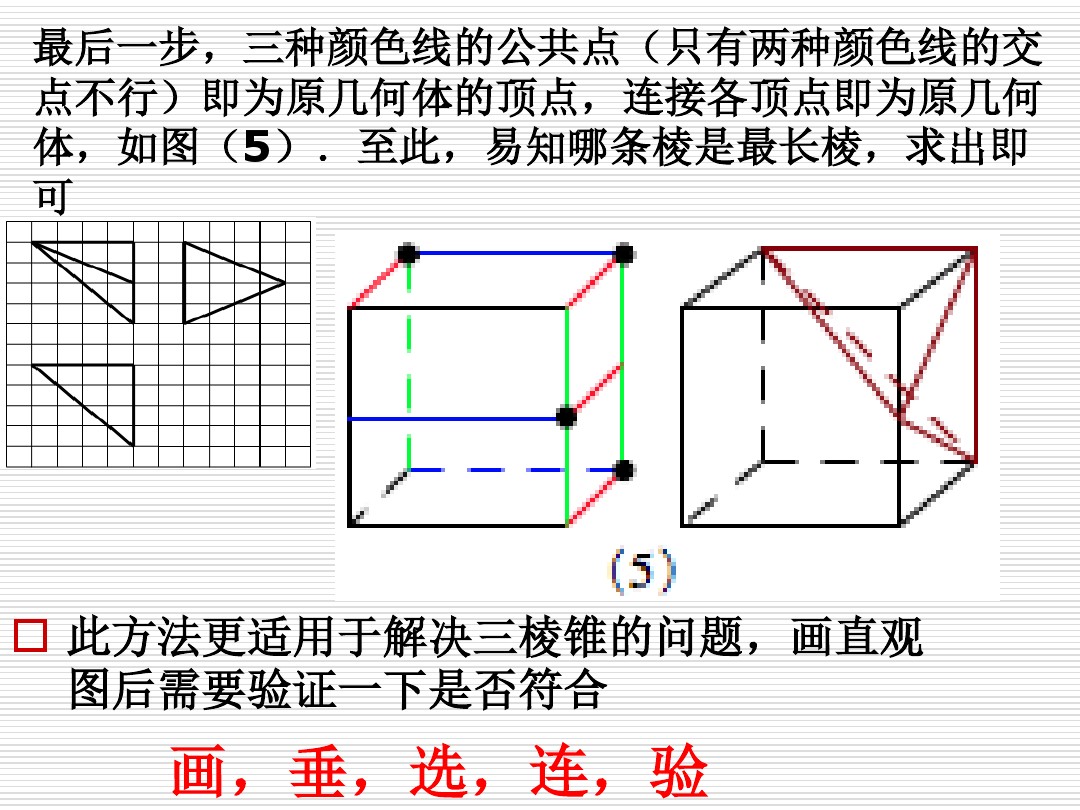
最后,确定出原几何体的各个顶点。我们这样做,从图中找出来由三条有色加粗的线段交汇的点(如果仅仅由两个颜色的线段交汇的点舍弃不用),将得到的这些点相连就得到了如下图的几何体,至此,完成了由三视图到几何体的直观图的还原过程。
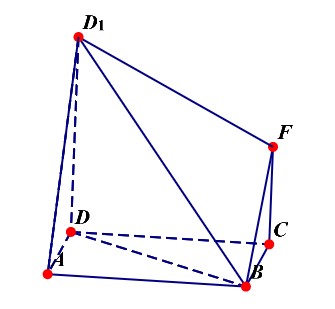
如图所示,连结(BD),则原几何体即可以看成一个三棱锥(D_1-ABD)和一个四棱锥(B-CDD_1F)合体构成的一个几何体,故其体积计算如下:
(V=V_{三棱锥D_1-ABD}+V_{四棱锥B-CDD_1F})
(=cfrac{1}{3} imes cfrac{1}{2} imes 2 imes 2 imes 2+cfrac{1}{3} imes cfrac{1}{2} imes(1+2) imes 2 imes 2=cfrac{10}{3})。
分析:
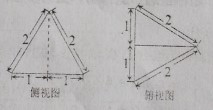
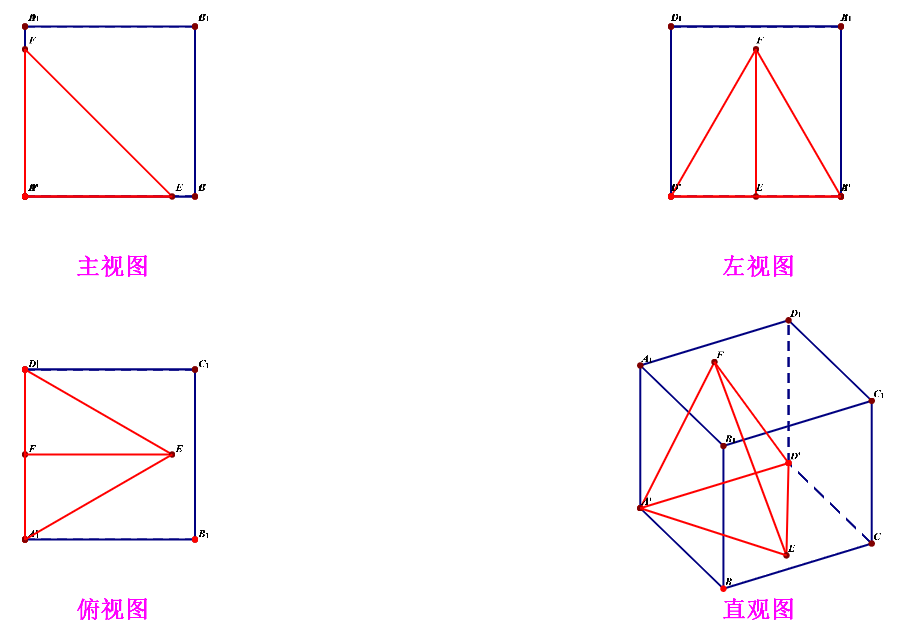
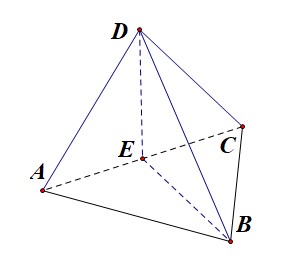
由图可知,实物图为三棱锥(D-ABC),且有(AB=BC=CD=AD=2),(AE=CE=1),(angle BED=cfrac{pi}{2}),面(ADCperp)面(ABC),故可求得(DE=BE=sqrt{3}),则最长的侧棱(BD)与底面所成的角为可知(angle DBE=45^{circ})。
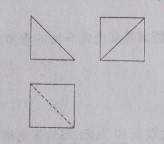
分析:如图所示,三视图的实物图可以从正方体中得到,是四棱锥(D-A_1BCD_1),故其外接球的直径为(A_1C=BD_1=sqrt{3}),则半径为(R=cfrac{sqrt{3}}{2}),表面积为(S=4pi R^2=3pi),故选(A)。