自己动手实现java数据结构（六）二叉搜索树

1.二叉搜索树介绍

　　前面我们已经介绍过了向量和链表。有序向量可以以二分查找的方式高效的查找特定元素，而缺点是插入删除的效率较低(需要整体移动内部元素)；链表的优点在于插入，删除元素时效率较高，但由于不支持随机访问，特定元素的查找效率为线性复杂度O(n)，效率较低。

　　向量和链表的优缺点是互补的，那么有没有办法兼具两者的优点呢？这便引出了接下来需要介绍的数据结构——二叉搜索树(Binary Search Tree)。

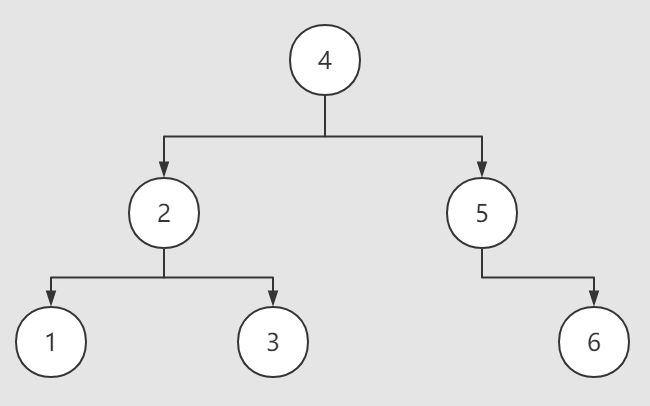
　　二叉搜索树和链表类似，同样是以节点为单位存储数据的链式数据结构。二叉搜索树作为一种树形数据结构，内部维护着一个根节点，在插入新数据时，会不断的和当前子树的根节点进行key值的大小比较，较小的key值落在左子树，较大的key值落在右子树，使得二叉搜索树从左到右维持一个有序的状态。

形式化的定义：

　　二叉搜索树的左子树上结点的值均小于根结点的值；右子树上结点的值均大于根结点的值；二叉搜索树的左、右子树也分别为二叉搜索树。

　　由于二叉搜索树中的数据是有序存储的，可以使用高效的二分查找查询特定元素；同时由于内部存储结构为链式节点，在插入、删除元素时的效率和链表类似，也十分高效。

　　可以说，二叉搜索树兼具了向量和链表的优点。

2.二叉搜索树ADT接口

　　二叉搜索树同样是一个存储key/value类型数据结构，因此和哈希表实现共用同一个接口（Map）。K/V数据结构需要暴露出内部节点的Key，value给用户灵活的访问，但哈希表和二叉搜索树的内部节点实现有一定的差异，所以在Map接口中暴露了Map.EntryNode接口，由哈希表和二叉搜索树的内部节点分别实现Map.EntryNode接口。

public interface Map <K,V>{
    /**
     * 存入键值对
     * @param key   key值
     * @param value value
     * @return 被覆盖的的value值
     */
    V put(K key,V value);

    /**
     * 移除键值对
     * @param key   key值
     * @return 被删除的value的值
     */
    V remove(K key);

    /**
     * 获取key对应的value值
     * @param key   key值
     * @return      对应的value值
     */
    V get(K key);

    /**
     * 是否包含当前key值
     * @param key   key值
     * @return      true：包含 false：不包含
     */
    boolean containsKey(K key);

    /**
     * 是否包含当前value值
     * @param value   value值
     * @return        true：包含 false：不包含
     */
    boolean containsValue(V value);

    /**
     * 获得当前map存储的键值对数量
     * @return 键值对数量
     * */
    int size();

    /**
     * 当前map是否为空
     * @return  true：为空 false：不为空
     */
    boolean isEmpty();

    /**
     * 清空当前map
     */
    void clear();

    /**
     * 获得迭代器
     * @return 迭代器对象
     */
    Iterator<EntryNode<K,V>> iterator();

    /**
     * entry 键值对节点接口
     * */
    interface EntryNode<K,V>{
        /**
         * 获得key值
         * */
        K getKey();

        /**
         * 获得value值
         * */
        V getValue();

        /**
         * 设置value值
         * */
        void setValue(V value);
    }
}

3.二叉搜索树实现细节

3.1 二叉搜索树基本属性

　　值得一提的是，二叉搜索树通过给存储的元素进行排序来加快查询的速度(遍历查询 ---> 二分查询)。

　　java是面向对象的语言，二叉搜索树中的元素不仅仅是整数、小数。如果说对于整数、小数甚至字符串的排序，我们确定了一个公认的排序逻辑。但是用户自定义的对象，例如小猫、小狗对象的排序可就仁者见仁智者见智了。

　　由于java并不支持比较符号">"，"<"的运算符重载，因此我们提供了一个比较排序的接口，用户可以在二叉搜索树初始化时指定排序时元素间比较的逻辑，使得二叉搜索树能以满足用户需求的方式执行排序的逻辑。

比较器接口(Comparator)定义：

@FunctionalInterface
public interface Comparator<T> {
    /**
     * 比较方法逻辑
     * @param o1    参数1
     * @param o2    参数2
     * @return      返回值大于0 ---> (o1 > o2)
     *              返回值等于0 ---> (o1 = o2)
     *              返回值小于0 ---> (o1 < o2)
     */
    int compare(T o1, T o2);
}

基本属性:

public class TreeMap<K,V> implements Map<K,V>{

    /**
     * 根节点
     * */
    private EntryNode<K,V> root;

    /**
     * 比较器(初始化之后，不能改)
     * */
    private final Comparator<? super K> comparator;

    /**
     * 当前二叉树的大小
     * */
    private int size;

    /**
     * 默认构造函数
     * */
    public TreeMap() {
        this.comparator = null;
    }

    /**
     * 指定了比较器的构造函数
     * */
    public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
    }
｝

3.2 二叉搜索树内部节点

　　二叉搜索树的内部节点除了必须的key，value字段，同时还维护了左、右孩子节点和双亲节点的引用。

　　通过实现暴露出去的Map.EntryNode接口，允许用户访问内部节点的key、value值，但二叉搜索树节点内部的孩子、双亲节点的引用是被封装起来的，外部用户是无法感知，也无需了解的。

   /**
     * 二叉搜索树 内部节点
     * */
    static class EntryNode<K,V> implements Map.EntryNode<K,V>{
        /**
         * key值
         * */
        K key;
        
        /**
         * value值
         * */
        V value;
        
        /**
         * 左孩子节点
         * */
        EntryNode<K,V> left;

        /**
         * 右孩子节点
         * */
        EntryNode<K,V> right;

        /**
         * 双亲节点
         * */
        EntryNode<K,V> parent;

        EntryNode(K key, V value) {
            this.key = key;
            this.value = value;
        }

        EntryNode(K key, V value,EntryNode<K,V> parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }

        @Override
        public K getKey() {
            return key;
        }

        @Override
        public V getValue() {
            return value;
        }

        @Override
        public void setValue(V value) {
            this.value = value;
        }

        @Override
        public String toString() {
            return key + "=" + value;
        }
    }

3.3 二叉搜索树内部辅助函数

　　为了简化代码逻辑以及去除重复代码，在实现过程中提取出了诸如：获取第一个节点(getFirst)、获取节点直接后继(getSuccessor)、获得key值对应目标节点(getTargetEntryNode)等等辅助方法。

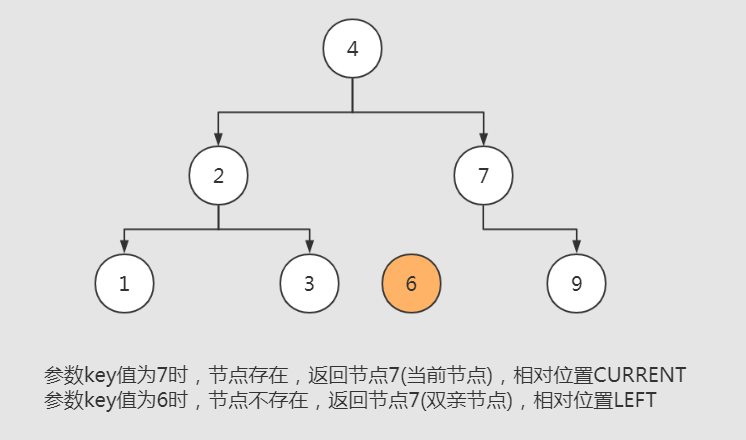
　　getTargetEntryNode用于获取key值对应的目标节点，运用了哨兵的思想。从根节点开始，使用二分查找的方式逐步逼近key值对应目标节点的位置。

　　如果目标节点确实存在，自然直接返回目标节点的引用(相对位置：RelativePosition.CURRENT)；

　　当目标节点不存在时，则假设目标节点已经存在(哨兵节点)，返回哨兵节点的双亲节点引用以及哨兵节点的相对位置(左、右节点：RelativePosition.LEFT、RelativePosition.Right)。

   /**
     * target 和目标节点的相对位置
     * */
    private enum RelativePosition {
        /**
         * 左节点
         * */
        LEFT,

        /**
         * 右节点
         * */
        RIGHT,

        /**
         * 当前节点
         * */
        CURRENT;
    }

 　　/**
     * 查找目标节点 返回值
     * */
    private static class TargetEntryNode<K,V>{
        /**
         * 目标节点
         * */
        private EntryNode<K,V> target;

        /**
         * 目标节点的双亲节点
         * */
        private EntryNode<K,V> parent;

        /**
         * 相对位置
         * */
        private RelativePosition relativePosition;

        TargetEntryNode(EntryNode<K, V> target, EntryNode<K, V> parent, RelativePosition relativePosition) {
            this.target = target;
            this.parent = parent;
            this.relativePosition = relativePosition;
        }
    }

 　　/**
     * 获得key对应的目标节点
     * @param key   对应的key
     * @return      对应的目标节点
     *               返回null代表 目标节点不存在
     * */
    private TargetEntryNode<K,V> getTargetEntryNode(K key){
        int compareResult = 0;
        EntryNode<K,V> parent = null;
        EntryNode<K,V> currentNode = this.root;
        while(currentNode != null){
            parent = currentNode;
            //:::当前key 和 currentNode.key进行比较
            compareResult = compare(key,currentNode.key);
            if(compareResult > 0){
                //:::当前key 大于currentNode 指向右边节点
                currentNode = currentNode.right;
            }else if(compareResult < 0){
                //:::当前key 小于currentNode 指向右边节点
                currentNode = currentNode.left;
            }else{
                return new TargetEntryNode<>(currentNode, parent, RelativePosition.CURRENT);
            }
        }

        //:::没有找到目标节点
        if(compareResult > 0){
            //:::返回 右孩子 哨兵节点
            return new TargetEntryNode<>(null, parent, RelativePosition.RIGHT);
        }else if(compareResult < 0){
            //:::返回 左孩子 哨兵节点
            return new TargetEntryNode<>(null, parent, RelativePosition.LEFT);
        }else{
            throw new RuntimeException("状态异常");
        }
    }

    /**
     * key值进行比较
     * */
    @SuppressWarnings("unchecked")
    private int compare(K k1,K k2){
        //:::迭代器不存在
        if(this.comparator == null){
            //:::依赖对象本身的 Comparable，可能会转型失败
            return ((Comparable) k1).compareTo(k2);
        }else{
            //:::通过迭代器逻辑进行比较
            return this.comparator.compare(k1,k2);
        }
    }

 　　/**
     * 判断双亲节点和目标节点 相对位置
     * @param parent    双亲节点
     * @param target    目标节点
     * @return          相对位置(左孩子/右孩子)
     */
    private RelativePosition getRelativeByParent(EntryNode<K,V> parent,EntryNode<K,V> target){
        if(parent.left == target){
            return RelativePosition.LEFT;
        }else if(parent.right == target){
            return RelativePosition.RIGHT;
        }else{
            throw new RuntimeException("不是父子节点关系");
        }
    }

    /**
     * 获得当前节点的直接后继
     * @param targetEntryNode     当前节点
     * @return              当前节点的直接后继
     */
    private EntryNode<K,V> getSuccessor(EntryNode<K,V> targetEntryNode){
        if(targetEntryNode == null){
            //:::当前节点为null，则后继也为null
            return null;
        }

        //:::判断当前节点是否存在右孩子
        if(targetEntryNode.right != null){
            //:::存在右孩子，右子树的最左节点为直接后继
            EntryNode<K,V> rightChildSuccessor = targetEntryNode.right;

            //:::循环往复，直至直接右孩子的最左节点
            while(rightChildSuccessor.left != null){
                rightChildSuccessor = rightChildSuccessor.left;
            }

            return rightChildSuccessor;
        }else{
            //:::不存在右孩子，寻找第一个靠右的双亲节点
            EntryNode<K,V> parent = targetEntryNode.parent;
            EntryNode<K,V> child = targetEntryNode;

            //:::判断当前孩子节点是否是双亲节点的左孩子
            while(parent != null && parent.right == child){
                //:::不是左孩子，而是右孩子，继续向上寻找
                child = parent;
                parent = parent.parent;
            }

            return parent;
        }
    }
    
    /**
     * 获得二叉搜索树的第一个节点
     * */
    private EntryNode<K,V> getFirstNode(){
        if(this.root == null){
            //:::空树，返回null
            return null;
        }

        EntryNode<K,V> entryNode = this.root;

        //:::循环往复，寻找整棵树的最左节点(最小节点、第一个节点)
        while(entryNode.left != null){
            entryNode = entryNode.left;
        }
        return entryNode;
    }

3.4 二叉搜索树插入接口实现

　　二叉搜索树的插入接口复用了前面提到的getTargetEntryNode方法，以二分查找的方式进行查询。

　　当key值对应的目标节点存在时，替换掉之前的value。

　　当key值对应的目标节点不存在时，运用哨兵的思想，通过双亲节点和哨兵节点的相对位置，在目标位置插入一个新的节点。

    @Override
    public V put(K key, V value) {
        if(this.root == null){
            this.root = new EntryNode<>(key,value);
            this.size++;
            return null;
        }

        //:::获得目标节点
        TargetEntryNode<K,V> targetEntryNode = getTargetEntryNode(key);
        if(targetEntryNode.relativePosition == RelativePosition.CURRENT){
            //:::目标节点存在于当前容器

            //:::暂存之前的value
            V oldValue = targetEntryNode.target.value;
            //:::替换为新的value
            targetEntryNode.target.value = value;
            //:::返回之前的value
            return oldValue;
        }else{
            //:::目标节点不存在于当前容器
            EntryNode<K,V> parent = targetEntryNode.parent;
            if(targetEntryNode.relativePosition == RelativePosition.LEFT){
                //:::目标节点位于左边
                parent.left = new EntryNode<>(key,value,parent);
            }else{
                //:::目标节点位于右边
                parent.right = new EntryNode<>(key,value,parent);
            }

            this.size++;
            return null;
        }
    }

3.5 二叉搜索树删除接口实现

　　二叉搜索树节点在被删除时，被删除节点存在三种情况：

1.不存在任何孩子节点(既没有左孩子，也没有右孩子)

　　直接将双亲节点和当前节点的连接切断(双亲对应孩子节点引用置为null)。

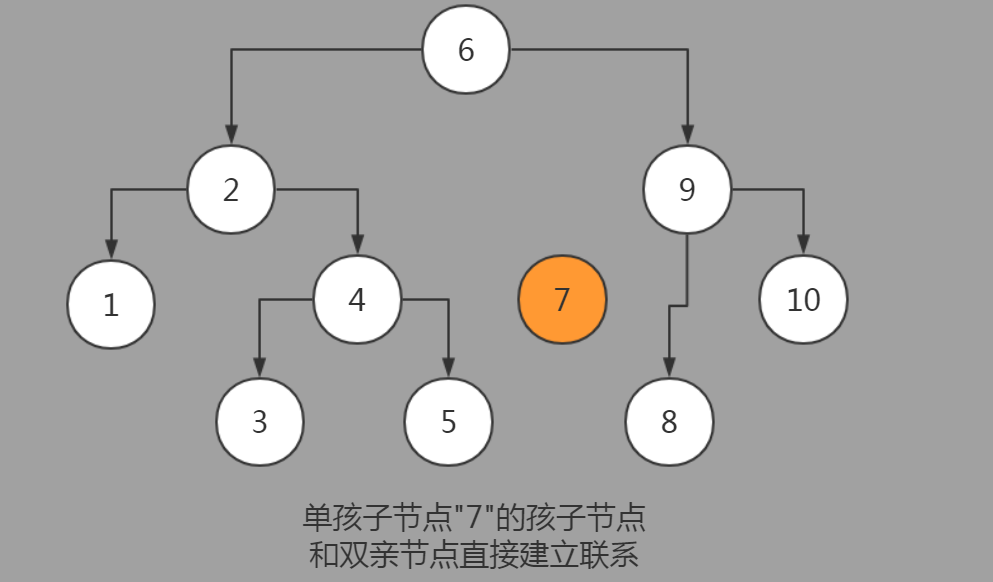
2.只存在一个孩子节点(只存在左孩子或者只存在右孩子)

　　被删除节点唯一的孩子节点代替被删除节点本身，唯一的孩子节点和双亲节点直接相连。

3.既有左孩子节点，又有右孩子节点

　　找到被删除节点的直接后继节点(直接前驱节点也行，本质上是保证删除之后依然保证有序性)，将被删除节点和其直接后继交换位置。

　　当右孩子节点存在时，直接后继节点必定存在于右子树中，并且其直接后继一定不存在左孩子节点(否则就不是直接后继节点了)，因此被删除节点的直接后继节点至多只存在一个右孩子节点(或没有任何孩子节点)。在两者交换位置后，可以转换为第一或第二种情况进行处理。　

节点删除前：

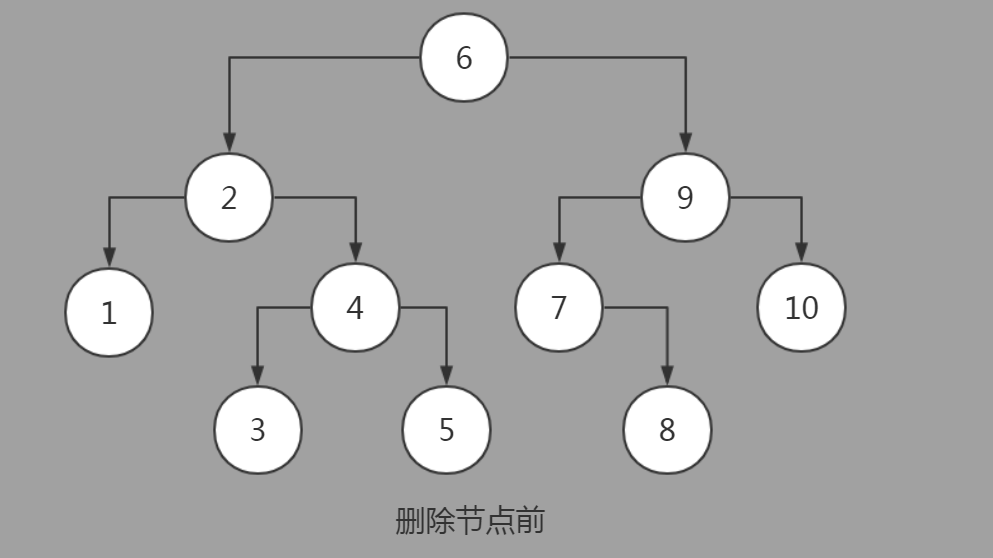
1.无孩子节点的删除：

2. 只有一个孩子节点的删除：

3. 拥有两个孩子的节点的删除：

二叉搜索树节点删除代码实现：

    @Override
    public V remove(K key) {
        if(this.root == null){
            return null;
        }

        //:::查询目标节点
        TargetEntryNode<K,V> targetEntryNode = getTargetEntryNode(key);
        if(targetEntryNode.relativePosition != RelativePosition.CURRENT){
            //:::没有找到目标节点
            return null;
        }else{
            //:::找到了目标节点

            //:::从二叉树中删除目标节点
            deleteEntryNode(targetEntryNode.target);

　　　　　　  return targetEntryNode.target.value;
        }
    }

   /**
     * 将目标节点从二叉搜索树中删除
     * @param target 需要被删除的节点
     * */
    void deleteEntryNode(EntryNode<K,V> target){
        /*
         * 删除二叉搜索树节点
         *     1.无左右孩子
         *         直接删除
         *     2.只有左孩子或者右孩子
         *         将唯一的孩子和parent节点直接相连
         *     3.既有左孩子，又有右孩子
         *         找到自己的直接前驱/后继（左侧的最右节点/右侧的最左节点）
         *         将自己和直接后继进行交换，转换为第1或第2种情况，并将自己删除
         * */

        //:::size自减1
        this.size--;

        //:::既有左孩子，又有右孩子
        if(target.left != null && target.right != null){
            //:::找到直接后继(右侧的最左节点)
            EntryNode<K,V> targetSuccessor = getSuccessor(target);

            //:::target的key/value和自己的后继交换
            target.key = targetSuccessor.key;
            target.value = targetSuccessor.value;
            //:::target指向自己的后继，转换为第一/第二种情况
            target = targetSuccessor;
        }

        EntryNode<K,V> parent = target.parent;
        //:::获得代替被删除节点原先位置的节点(从左右孩子中选择一个)
        EntryNode<K,V> replacement = (target.left != null ? target.left : target.right);

        if(replacement == null){
            //:::无左右孩子

            //:::被删除的target是根节点，且无左右孩子
            if(parent == null){
                //:::全树置空
                this.root = null;
            }else{
                RelativePosition relativePosition = getRelativeByParent(parent,target);

                //:::直接删除,断开和双亲节点的联系
                if(relativePosition == RelativePosition.LEFT){
                    parent.left = null;
                }else{
                    parent.right = null;
                }

                target.parent = null;
            }
        }else{
            //:::只有左孩子或者右孩子

            //:::被删除的target是根节点，且只有左孩子或者右孩子
            if(target.parent == null){
                //:::将存在的子树孩子节点，设置为根节点
                this.root = replacement;
            }else{
                replacement.parent = target.parent;

                RelativePosition relativePosition = getRelativeByParent(parent,target);

                //:::被删除节点的双亲节点指向被代替的节点
                if(relativePosition == RelativePosition.LEFT){
                    parent.left = replacement;
                }else{
                    parent.right = replacement;
                }
            }
        }
    }

3.6 二叉搜索树查询接口实现

　　二叉搜索树的查询接口使用了getTargetEntryNode方法。

　　当返回的相对位置为Current时，代表找到了目标节点，直接返回value；反之代表目标节点不存在，返回null。

    @Override
    public V get(K key) {
        if(this.root == null){
            return null;
        }

        //:::查询目标节点
        TargetEntryNode<K,V> targetEntryNode = getTargetEntryNode(key);
        if(targetEntryNode.relativePosition != RelativePosition.CURRENT){
            //:::没有找到目标节点
            return null;
        }else{
            return targetEntryNode.target.value;
        }
    }

3.7 二叉搜索树其它接口实现

    @Override
    public boolean containsKey(K key) {
        return (get(key) != null);
    }

    @Override
    public boolean containsValue(V value) {
        //:::寻找到第一个节点
        EntryNode<K,V> entryNode = getFirstNode();

        //:::从第一个节点开始，遍历整颗二叉搜索树
        while(entryNode != null){
            if(Objects.equals(entryNode.value,value)){
                //:::当前节点value匹配，返回true
                return true;
            }else{
                //:::指向下一个直接后继节点
                entryNode = getSuccessor(entryNode);
            }
        }

        //:::遍历整颗树之后，还未匹配，返回false
        return false;
    }

    @Override
    public int size() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        return (this.size == 0);
    }

    @Override
    public void clear() {
        this.size = 0;
        this.root = null;
    }

    @Override
    public String toString(){
        Iterator<Map.EntryNode<K,V>> iterator = this.iterator();

        //:::空容器
        if(!iterator.hasNext()){
            return "[]";
        }

        //:::容器起始使用"["
        StringBuilder s = new StringBuilder("[");

        //:::反复迭代
        while(true){
            //:::获得迭代的当前元素
            Map.EntryNode<K,V> data = iterator.next();

            //:::判断当前元素是否是最后一个元素
            if(!iterator.hasNext()){
                //:::是最后一个元素，用"]"收尾
                s.append(data).append("]");
                //:::返回 拼接完毕的字符串
                return s.toString();
            }else{
                //:::不是最后一个元素
                //:::使用", "分割，拼接到后面
                s.append(data).append(", ");
            }
        }
    }

    @Override
    public Iterator<Map.EntryNode<K, V>> iterator() {
        return new Itr();
    }

4.二叉搜索树迭代器

　　1. 二叉搜索树从最左节点开始，以中序遍历的方式遍历整颗树

　　2. 在迭代器初始化时，迭代器指向最小的节点(也就是最左节点)

　　3. 迭代器迭代时，下一个节点总是指向当前节点的直接后继

  /**
     * 二叉搜索树 迭代器实现
     * */
    private class Itr implements Iterator<Map.EntryNode<K,V>>{
        /**
         * 当前迭代节点
         * */
        private EntryNode<K,V> currentNode;

        /**
         * 下一个节点
         * */
        private EntryNode<K,V> nextNode;

        private Itr() {
            //:::初始化时，nextNode指向第一个节点
            this.nextNode = TreeMap.this.getFirstNode();
        }

        @Override
        public boolean hasNext() {
            return (this.nextNode != null);
        }

        @Override
        public Map.EntryNode<K, V> next() {
            this.currentNode = this.nextNode;

            this.nextNode = TreeMap.this.getSuccessor(this.nextNode);

            return this.currentNode;
        }

        @Override
        public void remove() {
            if(this.currentNode == null){
                throw new IteratorStateErrorException("迭代器状态异常: 可能在一次迭代中进行了多次remove操作");
            }

            //:::判断当前被删除的节点是否同时存在左右孩子
            if(this.currentNode.left != null && this.currentNode.right != null){
                /*
                    同时存在左右孩子的节点删除时当前节点会和直接后继(nextNode)进行交换
                    因此nextNode指向当前节点
                 */
                this.nextNode = this.currentNode;
            }
            //:::删除当前节点
            TreeMap.this.deleteEntryNode(this.currentNode);

            //:::currentNode设置为null，防止反复调用remove方法
            this.currentNode = null;
        }
    }

5.二叉搜索树性能

5.1 空间效率

　　二叉搜索树的内部节点除了key，value的引用，同时还维护着双亲，左右孩子节点的引用(不一定存在)，因此其空间效率比链表稍差，更是不如向量结构紧凑。但是这一点点空间效率的损失，带来的是二叉搜索树全面而优异的增删改查效率。

5.2 时间效率

　　二叉搜索树的插入，删除依赖于查询接口，而查询接口是以二分查找的方式实现的。在理想状态下(平衡的)，二叉搜索树的增删改查接口的效率为(O(logN))，N为当前二叉搜索树存储的元素总数；也可以说，二叉搜索树增删改查接口的效率正比于二叉搜索树的高度。

6.二叉搜索树总结

6.1 当前版本缺陷：

　　至此，我们实现了一个最基础的二叉搜索树，但还存在一个致命缺陷：

　　二叉搜索树在插入数据时，以二分查找的方式确定插入的位置。但是当插入数据的数据不够随机时，会降低二叉搜索树的查询效率。举个极端例子，当按照顺序插入1到10000的元素以从小到大顺序插入，二叉搜索树将退化为一个一维的链表(极端不平衡)，查询效率从O(logN)急剧降低为O(n)。

　　我们希望在插入，删除元素时，通过及时的调整二叉搜索树结构，用一系列等价变换的操作，使二叉搜索树始终保持一个适度平衡的状态。我们称这样的二叉搜索树为平衡二叉搜索树(Balanced Binary Search Tree)，常见的平衡二叉搜索树有AVL树、红黑树等。

　　只有平衡二叉搜索树才能始终保证始终高效的查询效率(O(logN))，而不会因为极端数据集合的插入，造成效率的大幅降低。

6.2 完整代码

二叉搜索树ADT接口:

 1 /**
 2  * Map ADT接口
 3  */
 4 public interface Map <K,V>{
 5     /**
 6      * 存入键值对
 7      * @param key   key值
 8      * @param value value
 9      * @return 被覆盖的的value值
10      */
11     V put(K key,V value);
12 
13     /**
14      * 移除键值对
15      * @param key   key值
16      * @return 被删除的value的值
17      */
18     V remove(K key);
19 
20     /**
21      * 获取key对应的value值
22      * @param key   key值
23      * @return      对应的value值
24      */
25     V get(K key);
26 
27     /**
28      * 是否包含当前key值
29      * @param key   key值
30      * @return      true：包含 false：不包含
31      */
32     boolean containsKey(K key);
33 
34     /**
35      * 是否包含当前value值
36      * @param value   value值
37      * @return        true：包含 false：不包含
38      */
39     boolean containsValue(V value);
40 
41     /**
42      * 获得当前map存储的键值对数量
43      * @return 键值对数量
44      * */
45     int size();
46 
47     /**
48      * 当前map是否为空
49      * @return  true：为空 false：不为空
50      */
51     boolean isEmpty();
52 
53     /**
54      * 清空当前map
55      */
56     void clear();
57 
58     /**
59      * 获得迭代器
60      * @return 迭代器对象
61      */
62     Iterator<EntryNode<K,V>> iterator();
63 
64     /**
65      * entry 键值对节点接口
66      * */
67     interface EntryNode<K,V>{
68         /**
69          * 获得key值
70          * */
71         K getKey();
72 
73         /**
74          * 获得value值
75          * */
76         V getValue();
77 
78         /**
79          * 设置value值
80          * */
81         void setValue(V value);
82     }
83 }

View Code

二叉搜索树实现:

/**
 * 二叉搜索树实现
 */
public class TreeMap<K,V> implements Map<K,V>{

    /**
     * 根节点
     * */
    private EntryNode<K,V> root;

    /**
     * 比较器(初始化之后，不能改)
     * */
    private final Comparator<? super K> comparator;

    /**
     * 当前二叉树的大小
     * */
    private int size;

    /**
     * 默认构造函数
     * */
    public TreeMap() {
        this.comparator = null;
    }

    /**
     * 指定了比较器的构造函数
     * */
    public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
    }

    /**
     * target 和目标节点的相对位置
     * */
    private enum RelativePosition {
        /**
         * 左节点
         * */
        LEFT,

        /**
         * 右节点
         * */
        RIGHT,

        /**
         * 当前节点
         * */
        CURRENT;
    }

    /**
     * 二叉搜索树 内部节点
     * */
    static class EntryNode<K,V> implements Map.EntryNode<K,V>{
        /**
         * key值
         * */
        K key;

        /**
         * value值
         * */
        V value;

        /**
         * 左孩子节点
         * */
        EntryNode<K,V> left;

        /**
         * 右孩子节点
         * */
        EntryNode<K,V> right;

        /**
         * 双亲节点
         * */
        EntryNode<K,V> parent;

        EntryNode(K key, V value) {
            this.key = key;
            this.value = value;
        }

        EntryNode(K key, V value,EntryNode<K,V> parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }

        @Override
        public K getKey() {
            return key;
        }

        @Override
        public V getValue() {
            return value;
        }

        @Override
        public void setValue(V value) {
            this.value = value;
        }

        @Override
        public String toString() {
            return key + "=" + value;
        }
    }

    /**
     * 二叉搜索树 迭代器实现
     * */
    private class Itr implements Iterator<Map.EntryNode<K,V>>{
        /**
         * 当前迭代节点
         * */
        private EntryNode<K,V> currentNode;

        /**
         * 下一个节点
         * */
        private EntryNode<K,V> nextNode;

        private Itr() {
            //:::初始化时，nextNode指向第一个节点
            this.nextNode = TreeMap.this.getFirstNode();
        }

        @Override
        public boolean hasNext() {
            return (this.nextNode != null);
        }

        @Override
        public Map.EntryNode<K, V> next() {
            this.currentNode = this.nextNode;

            this.nextNode = TreeMap.this.getSuccessor(this.nextNode);

            return this.currentNode;
        }

        @Override
        public void remove() {
            if(this.currentNode == null){
                throw new IteratorStateErrorException("迭代器状态异常: 可能在一次迭代中进行了多次remove操作");
            }

            //:::判断当前被删除的节点是否同时存在左右孩子
            if(this.currentNode.left != null && this.currentNode.right != null){
                /*
                    同时存在左右孩子的节点删除时会和直接后继(nextNode)进行交换
                    因此nextNode指向当前节点
                 */
                this.nextNode = this.currentNode;
            }
            //:::删除当前节点
            TreeMap.this.deleteEntryNode(this.currentNode);

            //:::currentNode设置为null，防止反复调用remove方法
            this.currentNode = null;
        }
    }

    /**
     * 查找目标节点 返回值
     * */
    private static class TargetEntryNode<K,V>{
        /**
         * 目标节点
         * */
        private EntryNode<K,V> target;

        /**
         * 目标节点的双亲节点
         * */
        private EntryNode<K,V> parent;

        /**
         * 相对位置
         * */
        private RelativePosition relativePosition;

        TargetEntryNode(EntryNode<K, V> target, EntryNode<K, V> parent, RelativePosition relativePosition) {
            this.target = target;
            this.parent = parent;
            this.relativePosition = relativePosition;
        }
    }

    @Override
    public V put(K key, V value) {
        if(this.root == null){
            this.root = new EntryNode<>(key,value);
            this.size++;
            return null;
        }

        //:::获得目标节点
        TargetEntryNode<K,V> targetEntryNode = getTargetEntryNode(key);
        if(targetEntryNode.relativePosition == RelativePosition.CURRENT){
            //:::目标节点存在于当前容器

            //:::暂存之前的value
            V oldValue = targetEntryNode.target.value;
            //:::替换为新的value
            targetEntryNode.target.value = value;
            //:::返回之前的value
            return oldValue;
        }else{
            //:::目标节点不存在于当前容器
            EntryNode<K,V> parent = targetEntryNode.parent;
            if(targetEntryNode.relativePosition == RelativePosition.LEFT){
                //:::目标节点位于左边
                parent.left = new EntryNode<>(key,value,parent);
            }else{
                //:::目标节点位于右边
                parent.right = new EntryNode<>(key,value,parent);
            }

            this.size++;
            return null;
        }
    }

    @Override
    public V remove(K key) {
        if(this.root == null){
            return null;
        }

        //:::查询目标节点
        TargetEntryNode<K,V> targetEntryNode = getTargetEntryNode(key);
        if(targetEntryNode.relativePosition != RelativePosition.CURRENT){
            //:::没有找到目标节点
            return null;
        }else{
            //:::找到了目标节点

            //:::从二叉树中删除目标节点
            deleteEntryNode(targetEntryNode.target);

            return targetEntryNode.target.value;
        }
    }

    @Override
    public V get(K key) {
        if(this.root == null){
            return null;
        }

        //:::查询目标节点
        TargetEntryNode<K,V> targetEntryNode = getTargetEntryNode(key);
        if(targetEntryNode.relativePosition != RelativePosition.CURRENT){
            //:::没有找到目标节点
            return null;
        }else{
            return targetEntryNode.target.value;
        }
    }

    @Override
    public boolean containsKey(K key) {
        return (get(key) != null);
    }

    @Override
    public boolean containsValue(V value) {
        //:::寻找到第一个节点
        EntryNode<K,V> entryNode = getFirstNode();

        //:::从第一个节点开始，遍历整颗二叉搜索树
        while(entryNode != null){
            if(Objects.equals(entryNode.value,value)){
                //:::当前节点value匹配，返回true
                return true;
            }else{
                //:::指向下一个直接后继节点
                entryNode = getSuccessor(entryNode);
            }
        }

        //:::遍历整颗树之后，还未匹配，返回false
        return false;
    }

    @Override
    public int size() {
        return this.size;
    }

    @Override
    public boolean isEmpty() {
        return (this.size == 0);
    }

    @Override
    public void clear() {
        this.size = 0;
        this.root = null;
    }

    @Override
    public Iterator<Map.EntryNode<K, V>> iterator() {
        return new Itr();
    }

    @Override
    public String toString(){
        Iterator<Map.EntryNode<K,V>> iterator = this.iterator();

        //:::空容器
        if(!iterator.hasNext()){
            return "[]";
        }

        //:::容器起始使用"["
        StringBuilder s = new StringBuilder("[");

        //:::反复迭代
        while(true){
            //:::获得迭代的当前元素
            Map.EntryNode<K,V> data = iterator.next();

            //:::判断当前元素是否是最后一个元素
            if(!iterator.hasNext()){
                //:::是最后一个元素，用"]"收尾
                s.append(data).append("]");
                //:::返回 拼接完毕的字符串
                return s.toString();
            }else{
                //:::不是最后一个元素
                //:::使用", "分割，拼接到后面
                s.append(data).append(", ");
            }
        }
    }

    /**
     * 获得key对应的目标节点
     * @param key   对应的key
     * @return      对应的目标节点
     *               返回null代表 目标节点不存在
     * */
    private TargetEntryNode<K,V> getTargetEntryNode(K key){
        int compareResult = 0;
        EntryNode<K,V> parent = null;
        EntryNode<K,V> currentNode = this.root;
        while(currentNode != null){
            parent = currentNode;
            //:::当前key 和 currentNode.key进行比较
            compareResult = compare(key,currentNode.key);
            if(compareResult > 0){
                //:::当前key 大于currentNode 指向右边节点
                currentNode = currentNode.right;
            }else if(compareResult < 0){
                //:::当前key 小于currentNode 指向右边节点
                currentNode = currentNode.left;
            }else{
                return new TargetEntryNode<>(currentNode, parent, RelativePosition.CURRENT);
            }
        }

        //:::没有找到目标节点
        if(compareResult > 0){
            //:::返回 右孩子 哨兵节点
            return new TargetEntryNode<>(null, parent, RelativePosition.RIGHT);
        }else if(compareResult < 0){
            //:::返回 左孩子 哨兵节点
            return new TargetEntryNode<>(null, parent, RelativePosition.LEFT);
        }else{
            throw new RuntimeException("状态异常");
        }
    }

    /**
     * key值进行比较
     * */
    @SuppressWarnings("unchecked")
    private int compare(K k1,K k2){
        //:::迭代器不存在
        if(this.comparator == null){
            //:::依赖对象本身的 Comparable，可能会转型失败
            return ((Comparable) k1).compareTo(k2);
        }else{
            //:::通过迭代器逻辑进行比较
            return this.comparator.compare(k1,k2);
        }
    }

    /**
     * 将目标节点从二叉搜索树中删除
     * @param target 需要被删除的节点
     * */
    private void deleteEntryNode(EntryNode<K,V> target){
        /*
         * 删除二叉搜索树节点
         *     1.无左右孩子
         *         直接删除
         *     2.只有左孩子或者右孩子
         *         将唯一的孩子和parent节点直接相连
         *     3.既有左孩子，又有右孩子
         *         找到自己的直接前驱/后继（左侧的最右节点/右侧的最左节点）
         *         将自己和直接后继进行交换，转换为第1或第2种情况，并将自己删除
         * */

        //:::size自减1
        this.size--;

        //:::既有左孩子，又有右孩子
        if(target.left != null && target.right != null){
            //:::找到直接后继(右侧的最左节点)
            EntryNode<K,V> targetSuccessor = getSuccessor(target);

            //:::target的key/value和自己的后继交换
            target.key = targetSuccessor.key;
            target.value = targetSuccessor.value;
            //:::target指向自己的后继，转换为第一/第二种情况
            target = targetSuccessor;
        }

        EntryNode<K,V> parent = target.parent;
        RelativePosition relativePosition = getRelativeByParent(parent,target);
        //:::获得代替被删除节点原先位置的节点(从左右孩子中选择一个)
        EntryNode<K,V> replacement = (target.left != null ? target.left : target.right);
        if(replacement == null){
            //:::无左右孩子

            //:::直接删除,断开和双亲节点的联系
            if(relativePosition == RelativePosition.LEFT){
                parent.left = null;
            }else{
                parent.right = null;
            }

            target.parent = null;
        }else{
            //:::只有左孩子或者右孩子
            replacement.parent = target.parent;

            //:::被删除节点的双亲节点指向被代替的节点
            if(relativePosition == RelativePosition.LEFT){
                parent.left = replacement;
            }else{
                parent.right = replacement;
            }
        }
    }

    /**
     * 判断双亲节点和目标节点 相对位置
     * @param parent    双亲节点
     * @param target    目标节点
     * @return          相对位置(左孩子/右孩子)
     */
    private RelativePosition getRelativeByParent(EntryNode<K,V> parent,EntryNode<K,V> target){
        if(parent.left == target){
            return RelativePosition.LEFT;
        }else if(parent.right == target){
            return RelativePosition.RIGHT;
        }else{
            throw new RuntimeException("不是父子节点关系");
        }
    }

    /**
     * 获得当前节点的直接后继
     * @param targetEntryNode     当前节点
     * @return              当前节点的直接后继
     */
    private EntryNode<K,V> getSuccessor(EntryNode<K,V> targetEntryNode){
        if(targetEntryNode == null){
            //:::当前节点为null，则后继也为null
            return null;
        }

        //:::判断当前节点是否存在右孩子
        if(targetEntryNode.right != null){
            //:::存在右孩子，右子树的最左节点为直接后继
            EntryNode<K,V> rightChildSuccessor = targetEntryNode.right;

            //:::循环往复，直至直接右孩子的最左节点
            while(rightChildSuccessor.left != null){
                rightChildSuccessor = rightChildSuccessor.left;
            }

            return rightChildSuccessor;
        }else{
            //:::不存在右孩子，寻找第一个靠右的双亲节点
            EntryNode<K,V> parent = targetEntryNode.parent;
            EntryNode<K,V> child = targetEntryNode;

            //:::判断当前孩子节点是否是双亲节点的左孩子
            while(parent != null && parent.right == child){
                //:::不是左孩子，是右孩子，继续向上寻找
                child = parent;
                parent = parent.parent;
            }

            return parent;
        }
    }

    /**
     * 获得二叉搜索树的第一个节点
     * */
    private EntryNode<K,V> getFirstNode(){
        if(this.root == null){
            //:::空树，返回null
            return null;
        }

        EntryNode<K,V> entryNode = this.root;

        //:::循环往复，寻找整棵树的最左节点(最小节点、第一个节点)
        while(entryNode.left != null){
            entryNode = entryNode.left;
        }

        return entryNode;
    }
}