jump game II

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Your goal is to reach the last index in the minimum number of jumps.

For example:
Given array A = [2,3,1,1,4]

The minimum number of jumps to reach the last index is 2. (Jump 1 step from index 0 to 1, then 3 steps to the last index.)

Note:
You can assume that you can always reach the last index.

题目:给定一个非负整数数组，每个元素表示可以从该位置向后跳的最大长度。比如2，表示最多可以跳2格的距离，当然，也可以跳1格。求跳到最后一个元素最少需要跳多少步。如上面例子，2条一步到3，3跳一步（3格）到4。

jump game  是问能否到达最后一个位置，使用的贪心算法，转换成从开头能跳的最远距离。用一个全局变量表示能跳的最远距离，再维护一个变量表示当前位置最远能跳到哪里，全局变量取二者的最大值。（前提是要能跳到当前位置i<=max）。

对于这一题，首先，可以想到使用动态规划。用一个数组dp[]表示达到每个位置的最少步数。计算到达当前位置i的最少步数dp[i]时，因为是从前面一步跳过来的，遍历前面所有位置j，如果位置j能跳过的距离大于i(A[j]+j>=i)，则说明从j能够跳一步到达i，那么dp[i]=min(dp[i],dp[j]+1)。dp的初始值为MAX_VALUE，因为取最小值。跳多步能到达不用管，因为会跳到其他位置，属于其他位置的判断了。

见代码：

class Solution {
    public int jump(int[] nums) {
        if(nums==null||nums.length==0) return -1;
        if(nums.length==1) return 0;
        
        //使用一个dp[i]，存放到达i位置的最少步数。
        int[] dp=new int[nums.length];
        dp[0]=0;//开始就在0处，不用跳
        for(int i=1;i<dp.length;i++)
            dp[i]=Integer.MAX_VALUE;
        
        for(int i=1;i<nums.length;i++){
            //遍历前面所有位置能不能跳一步到达i。
            for(int j=i-1;j>=0;j--){
                if(nums[j]+j>=i)
                    dp[i]=Math.min(dp[i],dp[j]+1);
            }
            //这是顺便判断能不能到达i位置。这题其实不需要判断。因为 题目说不然能到达
            if(dp[i]==Integer.MAX_VALUE){
                return -1;
            }
        }
        return dp[nums.length-1];
    }
}

但是动态规划在leetcode上会超时。但是，在机试中，能做出来才是王道。。

这题另外一个方法就是使用贪心算法。这个有点难理解。仔细体会

先看代码，再解释。

        int ret=0;//ret表示最小步数
        
        int last=0;//表示ret步能到达的最远地方
        
        int cur=0;//表示从头开始到i位置,能到达的最远地方
        for(int i=0;i<nums.length&&i<=cur;i++){
            if(i>last){//当前步数能到的最远距离小于i，表示到不了i，该继续走一步
                ret++;  //这里加一步，是因为last能到i-1。所以ret一开始最远能到达i-1
                last=cur;//再跳一步，这一步是从i前面的任意位置开始跳，能跳到的最远距离也就是从头到i-1位置能到达的最远距离cur
          　　}  
　　　　　　cur=Math.max(cur,nums[i]+i);
        }
        if(cur<nums.length-1) return -1; //这里是判断能不能到达最后，可以省略，因为题目假定能到达
        return ret;

O(n)的。。。。#我和我的小伙伴们都惊呆了#。

要理解这个算法，首先明白，这个题只要我们求跳数，怎么跳，最后距离是多少，都没让求的。

大牛这个算法的思想主要是，扫描数组（废话。。。），以确定当前最远能覆盖的节点，放入curr。然后继续扫描，直到当前的路程超过了上一次算出的覆盖范围，也就是i>last ，那么说明之前last=i-1，这个时候就需要更新覆盖范围last，同时更新步数，步数只要加一步就行，这一步是在i-1或者之前开始跳的，所以这一步能到的最远距离也就是上一个位置i-1的cur。因为我们是经过了多一跳才能继续前进的。

形象地说，这个是在争取每跳最远的greedy。举个栗子。

比如就是我们题目中的[2,3,1,1,4]。初始状态是这样的：cur表示最远能覆盖到的地方，用红色表示。last表示已经覆盖的地方，用箭头表示。它们都指在第一个元素上。

接下来，第一元素告诉cur，最远咱可以走2步。于是：

下一循环中，i指向1（图中的元素3），发现，哦，i小于last能到的范围，于是更新last（相当于说，进入了新的势力范围），步数ret加1.同时要更新cur。因为最远距离发现了。

接下来，i继续前进，发现i在当前的势力范围内，无需更新last和步数ret。更新cur。

i继续前进，接下来发现超过当前势力范围，更新last和步数。cur已然最大了。

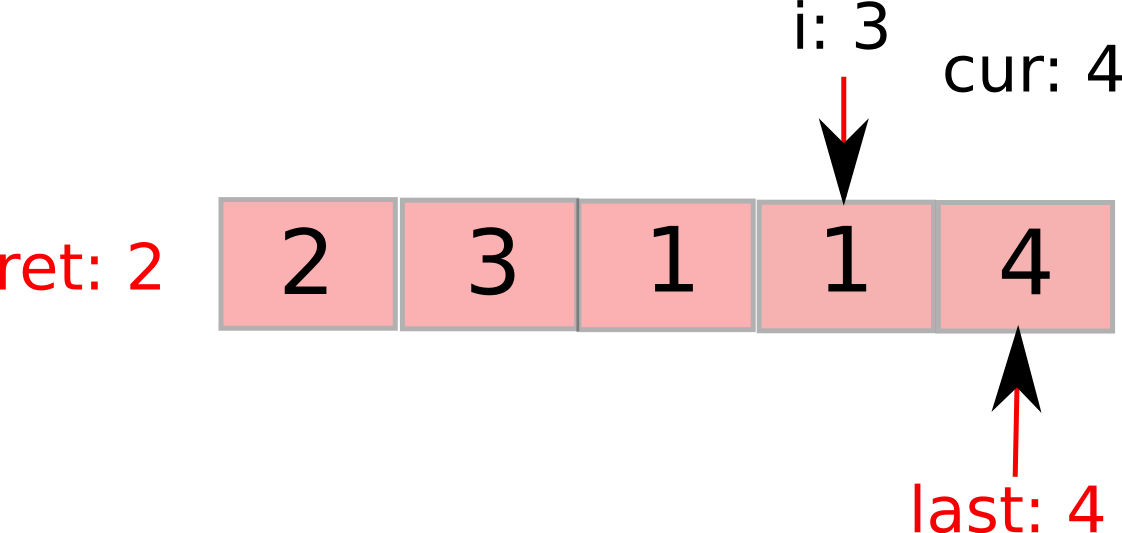
最后，i到最后一个元素。依然在势力范围内，遍历完成，返回ret。

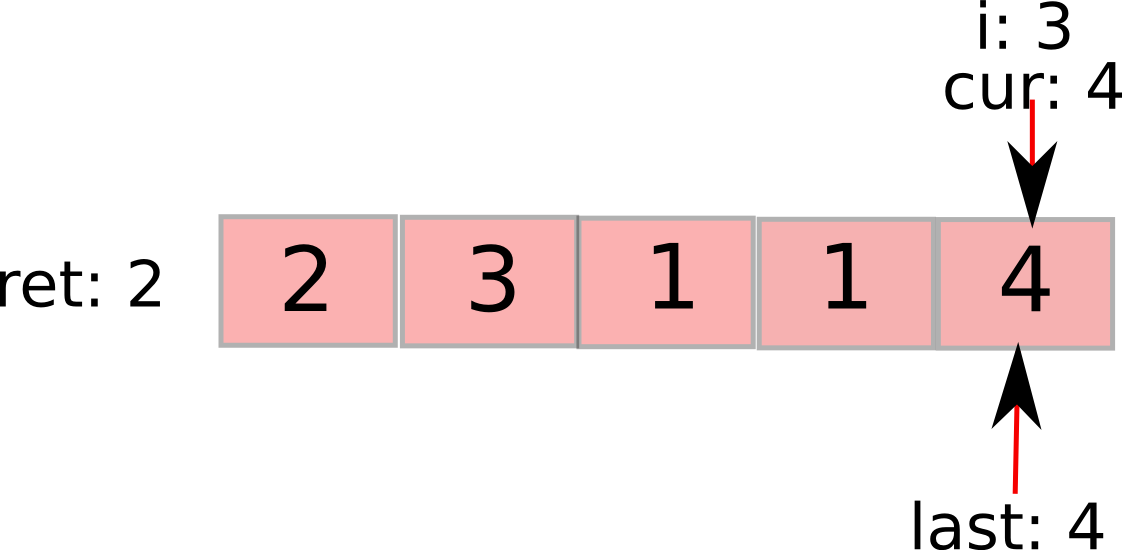
这道题让我们明白一个道理：

不要做无必要的计算。

对了，有同学会问，那为啥要用last，直接用curr跳不就行了。直接用curr跳那每次都是跳最远的，但是最优路径不不一定是这样。

参考：http://www.cnblogs.com/lichen782/p/leetcode_Jump_Game_II.html